Im Frühjahr 1996 liess ich mir diesen Schrank von einem Möbelschreiner anfertigen. Die Gestaltung der Vorderfront beruht auf einem mathematischen Muster aus Geraden und Halbkreisen, das unten auch noch einmal separat gezeigt ist. Mathematisch gesehen besitzt dieses Muster eine grosse Regelmässigkeit; viele Mathematiker werden es sofort wiedererkennen. Der graphische Künstler Maurits Cornelis Escher hat beeindruckende Werke auf der Basis dieses und ähnlicher Muster erstellt. Einen Teil der mathematischen Besonderheiten kann man ohne alle Vorkenntnisse verstehen.

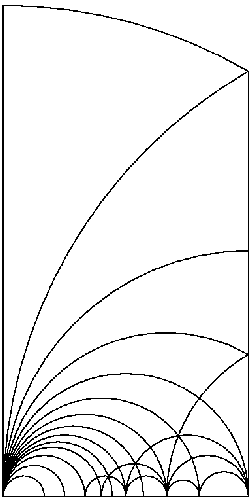
Der Schrank ist modular in zwei Bedeutungen. Erstens stammt das zugrundeliegende mathematische Muster aus dem Gebiet der Modulformen; die Symmetriegruppe des Musters heisst die Modulgruppe. Zweitens ist der Schrank auch im technischen Sinne modular aufgebaut: man kann ihn auseinandernehmen und jede kleinere Zahl von vertikalen Elementen alleine aufbauen.

Mathematischer Hintergrund

Das Muster besteht aus vertikalen Geraden sowie Halbkreisen, deren Mittelpunkte alle auf der unten liegenden horizontalen Achse liegen. Man sollte es sich als auf die ganze obere Halbebene periodisch ausgebreitet vorstellen. Ausserdem sollte man sich am unteren Rand unendlich viele, immer kleiner werdende Halbkreise dazu denken, die aus praktischen Gründen natürlich nicht gezeigt werden können. Eine Besonderheit dieses Musters liegt darin, dass die Linien sich nur auf ganz bestimmte regelmässige Weise treffen. Im Innern des Arrangements gibt nämlich nur zwei Arten von Schnittpunkten: Entweder es treffen sich genau zwei Linien im Winkel von 90 Grad, oder genau drei Linien im Winkel von jeweils 60 Grad. Am unteren Rand gehen dagegen stets unendlich viele Halbkreise von demselben Punkt aus. Ausserdem soll man sich vorstellen, dass sich alle vertikalen Geraden in einem unendlich fernen Punkt treffen.

Schneiden wir nun nun die Halbebene entlang aller dieser Linien auf, so ist jedes Teilstück ein gebogenes Dreieck, das von geraden Strecken oder Kreislinien begrenzt wird. Man sieht leicht, dass jedes Dreieck genau einen Winkel von 90 Grad, einen Winkel von 60 Grad, und einen Winkel von 0 Grad besitzt. Die Winkel von 0 Grad sind dabei diejenigen am unteren Rand, da die Linien sich dort tangential treffen. In gewissem Sinn sind daher alle diese Dreiecke ähnlich zueinander. (Dass die Winkelsumme im Dreieck nicht gleich 180 Grad ist, ist nur deshalb möglich, weil die Begrenzungslinien nicht gerade sein müssen.) Dieselben Aussagen gelten auch für die nach oben offenen Bereiche, da wir uns ja vorstellen, dass die Begrenzungsgeraden sich im Unendlichen treffen, und zwar wiederum im Winkel von 0 Grad.

Die interessanteste Eigenschaft des Musters besteht darin, dass es vollkommen in sich übergeht, wenn man an jeder seiner Linien spiegelt. Für die Spiegelung an einer vertikalen Geraden ist das offensichtlich. Das gab übrigens auch den Anlass dazu, den Schrank in jeweils spiegelsymmetrische vertikale Elemente zu gliedern. Die Spiegelung an einem Halbkreis ist nicht die übliche. Ohne sie präzise anzugeben, kann man sie sich etwa so vorstellen: Das Innere des Kreises wird nach aussen gestülpt, so dass sein Bild die ganze restliche Fläche überdeckt. Je näher ein Punkt am Mittelpunkt des Kreises liegt, desto weiter entfernt kommt sein Spiegelbild zu liegen und umso mehr wird die Umgebung des Punktes gedehnt. Umgekehrt wird das Äussere des Kreises ohne Falten in das Innere gedrückt; dabei wird natürlich umso mehr gestaucht, je weiter man vom Kreis entfernt war. Eine nützliche Eigenschaft dieser speziellen Art von Spiegelung liegt darin, dass jeder andere Kreis und jede Gerade wieder auf einen Kreis oder eine Gerade abgebildet wird. Insbesondere wird das Gesamtmuster auf sich abgebildet. Auch als Laie kann man sich davon überzeugen, dass die Konstellation, wie verschiedene Dreiecke aneinanderstossen, unter solchen Spiegelungen invariant ist.

In der mathematischen Fachsprache handelt es sich um eine Zerlegung der oberen Halbebene in Fundamentalbereiche unter der Operation der arithmetischen Gruppe GL(2,Z). Zwei benachbarte Glastüren zusammen bilden den üblichen Fundamentalbereich unter der Gruppe SL(2,Z). In komplexen Koordinaten lässt sich die Operation leicht beschreiben: Zwei Punkte z und w sind äquivalent genau dann, wenn es ganze Zahlen a, b, c, und d gibt mit ad-bc=+1 oder =-1, so dass w oder sein komplex Konjugiertes gleich (az+b)/(cz+d) ist.

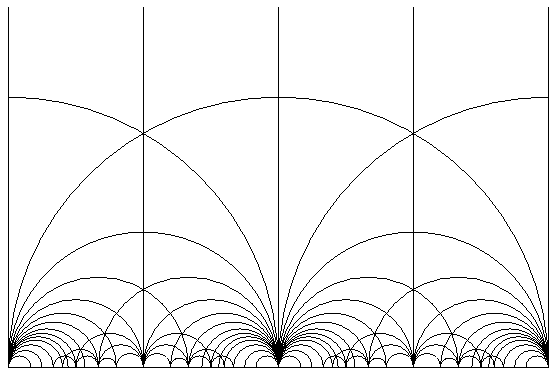
Die obere Halbebene trägt die Struktur einer sogenannten hyperbolischen Ebene, das heisst, einer bestimmten nicht-euklidischen Geometrie. Dabei ist der Abstand zweier Punkte anders definiert als gewöhnlich. So wie die Geraden in der üblichen euklidischen Geometrie charakterisiert werden können als die kürzeste Verbindung zwischen zwei Punkten, sind hier die kürzesten Verbindungen, genannt Geodätische, genau die vertikalen Geraden sowie die Halbkreise, deren Mittelpunkte auf der horizontalen Achse liegen. Alle Linien in dem beschriebenen Muster sind solche Geodätische.

Entwurf und Verarbeitung

Die Grundidee zu diesem Schrank hatte ich selbst. Mein Ziel war, einen ästhetisch ansprechenden Gebrauchsgegenstand mit einer tieferen mathematischen Bedeutung auf meinem Arbeitsgebiet zu realisieren. Nach eigenen Vorüberlegungen wurde das endgültige Konzept in ausführlicher Besprechung mit dem Schreinermeister Urban Brenner erarbeitet, der den Schrank in seiner Werkstatt dann auch herstellte.

Die Entscheidung für das beschriebene Linienmuster lag auf der Hand, gab es doch die Möglichkeit, zumindest einen Teil der Linien als natürliche Ränder von Türen zu realisieren. Jedes der 8 vertikalen Elemente des Schranks hat oben eine Glastür und unten eine Holztür. Während die oberen Türen je ein einzelnes hyperbolisches Dreieck repräsentieren, wurde das Dreiecksmuster auf den unteren Türen durch Intarsien verwirklicht. Eine Kreislinie als Begrenzung zwischen den beiden Türen drängte sich regelrecht auf; als schwarze Ader setzt sie sich auf den benachbarten Türen fort. Im Innern des Schranks wird die gebogene Oberkante der Holztür wieder aufgenommen durch ein ebenfalls kreisförmig gebogenes Brett. Die Einlagebretter darüber sind aus praktischen Gründen horizontal, wie üblich, auch wenn sie dadurch keine Entsprechung in dem ursprünglichen mathematischen Muster besitzen. Um dieses Muster trotzdem zur nötigen Geltung kommen zu lassen, wurden weitere Gestaltungselemente, von den Griffen abgesehen, ganz vermieden. Deshalb haben zum Beispiel die Glastüren keine Rahmen. Ausserdem half dieses Prinzip, die Kosten in einem vertretbaren Rahmen zu belassen.

Allein die gebogene Grenze zwischen den unteren und oberen Türen führte zu einigem technischen Mehraufwand bei der Herstellung des Schranks. Viele Arbeitsgänge (Zuschneiden, Verleimen des Furniers, Verleimen des gebogenen Bretts, etc.) mussten von Hand nach einer vorher gefertigten Form erfolgen. Die Verarbeitung der Holztüren mit der feinen Intarsienfront erforderte ausserdem äusserste Sorgfalt und Genauigkeit. Um im Fall einer Beschädigung eine Reserve zu haben, wurden im voraus gleich 10 Exemplare des Intarsienmusters bestellt. Diese Reserve wurde auch voll ausgeschöpft!

Die Intarsien selbst wurden von einem Spezialisten mit Hilfe einer computergesteuerten Laserfräse hergestellt, wodurch eine fast unglaubliche Präzision erreicht wurde. Jeweils ein Furnierblatt aus besonders strukturarmem kanadischem Ahorn und eines aus schwarz gebeiztem anderen Holz wurde mit dem Laser zerschnitten; die Einzelteile wurden dann von Hand zusammengesetzt und anschliessend verleimt. Das Resultat dieser hervorragenden Gesamtleistung können Sie besichtigen, wenn Sie mich zuhause besuchen.

Für weitere Fotos hier klicken

Kontakt

Bislang ist dieser Schrank weltweit ein Unikat, soweit ich weiss. Wenn Sie sich das gleiche oder ein ähnliches Objekt anfertigen lassen möchten, würde ich Sie gerne dabei unterstützen. Treten Sie dazu bitte mit mir oder der Schreinerei Urban Brenner in Verbindung. Eine kommerzielle Verwertung dieses Entwurfs behalten wir uns allerdings vor. Wenn Sie selbst Möbel oder andere schöne Gegenstände mit mathematischem Hintergrund kennen, oder Ideen dazu haben, würde ich mich über eine entsprechende Mitteilung freuen.
 

Richard Pink

Schreinerei Urban Brenner Siedlungsweg 7 D - 72202 Nagold Deutschland Tel.: +49-7452-4904 Fax: +49-7452-3865