arpackppTutorial.cc

This tutorial shows how to use Arpack++ to solve eigenvalue problems.

1. Commented program
   1. Preparations
   2. Standard eigenvalue problems
   3. General eigenvalue problems
   4. General, symmetric eigenvalue problems
2. Complete source code

Commented Program

Include files for eigenvalue solvers.

#include "eigensolver.hh"

Preparations

In the first lines three matrices are initialized. 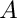is a general, complex matrix,

    concepts::SparseMatrix<concepts::Cmplx> A(4, 4);
 
    A(0, 0) = concepts::Cmplx(6, 6);
    A(0, 1) = concepts::Cmplx(7, 5);
    A(0, 2) = concepts::Cmplx(7, 10);
    A(0, 3) = concepts::Cmplx(10, 1);
 
    A(1, 0) = concepts::Cmplx(8, 9);
    A(1, 1) = concepts::Cmplx(3, 1);
    A(1, 2) = concepts::Cmplx(6, 9);
    A(1, 3) = concepts::Cmplx(5, 5);
 
    A(2, 0) = concepts::Cmplx(6, 9);
    A(2, 1) = concepts::Cmplx(2, 7);
    A(2, 2) = concepts::Cmplx(0, 5);
    A(2, 3) = concepts::Cmplx(4, 9);
 
    A(3, 0) = concepts::Cmplx(10, 2);
    A(3, 1) = concepts::Cmplx(9, 5);
    A(3, 2) = concepts::Cmplx(6, 5);
    A(3, 3) = concepts::Cmplx(5, 4);

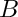is real, symmetric and positive definite,

    concepts::SparseMatrix<concepts::Real> B(4, 4);
 
    B(0, 0) = 6;
    B(0, 1) = 2;
    B(0, 2) = 1;
    B(0, 3) = 2;
 
    B(1, 0) = 2;
    B(1, 1) = 9;
    B(1, 2) = 1;
    B(1, 3) = 2;
 
    B(2, 0) = 1;
    B(2, 1) = 1;
    B(2, 2) = 9;
    B(2, 3) = 2;
 
    B(3, 0) = 2;
    B(3, 1) = 2;
    B(3, 2) = 2;
    B(3, 3) = 7;

and 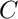is real and symmetric.

    concepts::SparseMatrix<concepts::Real> C(4, 4);
 
    C(0, 0) = 2;
    C(0, 1) = 1;
    C(0, 2) = 1;
    C(0, 3) = 1;
 
    C(1, 0) = 1;
    C(1, 1) = 1;
    C(1, 2) = 0;
    C(1, 3) = 1;
 
    C(2, 0) = 1;
    C(2, 1) = 0;
    C(2, 2) = 2;
    C(2, 3) = 1;
 
    C(3, 0) = 1;
    C(3, 1) = 1;
    C(3, 2) = 1;
    C(3, 3) = 0;

Standard eigenvalue problems

We solve the standard eigenvalue problem 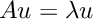using the class EasyArPackppStd. First we compute the two eigenvalues closest to zero using the shift and invert mode.

    eigensolver::EasyArPackppStd<concepts::Cmplx, concepts::Real> eacs(A, 2, 0.0);

We read the computed eigenvalues

    concepts::Array<concepts::Cmplx> eigenvalues = eacs.getSolver()->getEV();

and the corresponding eigenvectors.

    concepts::Array<concepts::Vector<concepts::Cmplx> *> eigenvectors = eacs.getSolver()->getEF();

We test the accuracy of the computed eigenvalues and eigenvectors.

    concepts::Vector<concepts::Cmplx> res1(eigenvectors[0]->size());
    concepts::Vector<concepts::Cmplx> res2(eigenvectors[0]->size());
    res1 = *eigenvectors[1];
    A(res1, res2);
    std::cout << "First residuum: " << ((res1 * eigenvalues[1]) - res2).l2() << std::endl;
    std::cout << "Eigenvalue with smallest distance to 0.0: " << eigenvalues[1] << std::endl;

Now we compute the two eigenvalues with largest magnitude using the regular mode.

    eigensolver::EasyArPackppStd<concepts::Cmplx, concepts::Real> eacs2(A, 2, (char*) "LM");

Again we read the computed eigenvalues

    eigenvalues = eacs2.getSolver()->getEV();

and the corresponding eigenvectors,

    eigenvectors = eacs2.getSolver()->getEF();

and test their accuracy.

    res1 = *eigenvectors[1];
    A(res1, res2);
    std::cout << "Second residuum: " << ((res1 * eigenvalues[1]) - res2).l2() << std::endl;
    std::cout << "Eigenvalue with largest magnitude:  " << eigenvalues[1] << std::endl;

General eigenvalue problems

Now let us solve the general eigenvalue problem 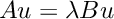. We use the class EasyArPackppGen for this purpose. First we compute the two eigenvalues closest to zero using the shift and invert mode.

    eigensolver::EasyArPackppGen<concepts::Cmplx, concepts::Real> eacg(A, B, 2, 0.0);

Again we read the computed eigenvalues

    eigenvalues = eacg.getSolver()->getEV();

and the corresponding eigenvectors,

    eigenvectors = eacg.getSolver()->getEF();

and test their accuracy.

    A((*eigenvectors[1]), res1);
    B((*eigenvectors[1]), res2);
    std::cout << "Third residuum: " << (res1 - (res2 * eigenvalues[1])).l2() << std::endl;
    std::cout << "Eigenvalue with smallest distance to 0.0: " << eigenvalues[1] << std::endl;

And then we compute the two eigenvalues with largest magnitude using the regular mode.

    eigensolver::EasyArPackppGen<concepts::Cmplx, concepts::Real> eacg2(A, B, 2, (char*) "LM");

Again we read the computed eigenvalues

    eigenvalues = eacg2.getSolver()->getEV();

and the corresponding eigenvectors,

    eigenvectors = eacg2.getSolver()->getEF();

and test their accuracy.

    A((*eigenvectors[1]), res1);
    B((*eigenvectors[1]), res2);
    std::cout << "Fourth residuum: " << (res1 - (res2 * eigenvalues[1])).l2() << std::endl;
    std::cout << "Eigenvalue with largest magnitude: " << eigenvalues[1] << std::endl;

General, symmetric eigenvalue problems

In our final example we want to solve the general, symmetric eigenvalue problem 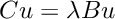, where the matrix 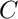is real and symmetric and the matrix 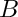is real, symmetric and positive definite. Using Octave we computed the eigenvalues

    double eigenvalue1 = -0.1691925951083604;
    double eigenvalue2 =  0.0619419844415557;
    double eigenvalue3 =  0.3841300911212291;

First we use the so-called Cayley mode of the class EasyArPackppSymGen to compute the eigenvalue closest to eigenvalue1

    eigensolver::EasyArPackppSymGen easg1(C, B, 1, eigenvalue1);

and print the difference of the Octave solution and the Arpack++ solution on the screen

    std::cout << "Difference of Octave solution and Arpack++ solution using Cayley mode: " 
        << (easg1.getSolver()->getEV())[0] - eigenvalue1 << std::endl;

We proceed similarly, when computing the eigenvalue closest to eigenvalue2 using the Buckling mode

    eigensolver::EasyArPackppSymGen easg2('B', C, B, 1, eigenvalue2);
    std::cout << "Difference of Octave solution and Arpack++ solution using Buckling mode: "
        << (easg2.getSolver()->getEV())[0] - eigenvalue2 << std::endl;

and when computing the eigenvalue closest to eigenvalue3 using the shift and invert mode

    eigensolver::EasyArPackppSymGen easg3('S', C, B, 1, eigenvalue3);
    std::cout << "Difference of Octave solution and Arpack++ solution using shift and invert mode: "
        << (easg3.getSolver()->getEV())[0] - eigenvalue3 << std::endl;

Complete Source Code

Author

Dirk Klindworth 2014

#include "eigensolver.hh"
#ifdef HAS_MPI
#include "mpi.h"
#endif
 
int main(int argc, char** argv) {
 
  
  concepts::Stacktrace::doit() = false;
 
  try {
 
#ifdef HAS_MPI
    MPI_Init(&argc, &argv);
#endif
 
  // ** preparations **
 
    // A is a general complex matrix
    // A = [     6 +  6i    7 +  5i    7 + 10i   10 +  1i
    //           8 +  9i    3 +  1i    6 +  9i    5 +  5i
    //           6 +  9i    2 +  7i    0 +  5i    4 +  9i
    //          10 +  2i    9 +  5i    6 +  5i    5 +  4i]
 
    concepts::SparseMatrix<concepts::Cmplx> A(4, 4);
 
    A(0, 0) = concepts::Cmplx(6, 6);
    A(0, 1) = concepts::Cmplx(7, 5);
    A(0, 2) = concepts::Cmplx(7, 10);
    A(0, 3) = concepts::Cmplx(10, 1);
 
    A(1, 0) = concepts::Cmplx(8, 9);
    A(1, 1) = concepts::Cmplx(3, 1);
    A(1, 2) = concepts::Cmplx(6, 9);
    A(1, 3) = concepts::Cmplx(5, 5);
 
    A(2, 0) = concepts::Cmplx(6, 9);
    A(2, 1) = concepts::Cmplx(2, 7);
    A(2, 2) = concepts::Cmplx(0, 5);
    A(2, 3) = concepts::Cmplx(4, 9);
 
    A(3, 0) = concepts::Cmplx(10, 2);
    A(3, 1) = concepts::Cmplx(9, 5);
    A(3, 2) = concepts::Cmplx(6, 5);
    A(3, 3) = concepts::Cmplx(5, 4);
 
    // B is a real, symmetric, positive definite matrix
    //         B =    [  6   2   1   2
    //                   2   9   1   2
    //                   1   1   9   2
    //                   2   2   2   7]
 
    concepts::SparseMatrix<concepts::Real> B(4, 4);
 
    B(0, 0) = 6;
    B(0, 1) = 2;
    B(0, 2) = 1;
    B(0, 3) = 2;
 
    B(1, 0) = 2;
    B(1, 1) = 9;
    B(1, 2) = 1;
    B(1, 3) = 2;
 
    B(2, 0) = 1;
    B(2, 1) = 1;
    B(2, 2) = 9;
    B(2, 3) = 2;
 
    B(3, 0) = 2;
    B(3, 1) = 2;
    B(3, 2) = 2;
    B(3, 3) = 7;
 
    //C is a symmetric matrix
    //C =
    //   2   1   1   1
    //   1   1   0   1
    //   1   0   2   1
    //   1   1   1   0
    concepts::SparseMatrix<concepts::Real> C(4, 4);
 
    C(0, 0) = 2;
    C(0, 1) = 1;
    C(0, 2) = 1;
    C(0, 3) = 1;
 
    C(1, 0) = 1;
    C(1, 1) = 1;
    C(1, 2) = 0;
    C(1, 3) = 1;
 
    C(2, 0) = 1;
    C(2, 1) = 0;
    C(2, 2) = 2;
    C(2, 3) = 1;
 
    C(3, 0) = 1;
    C(3, 1) = 1;
    C(3, 2) = 1;
    C(3, 3) = 0;
    
 
    // ** use EasyArpackppStd to solve standard eigenproblems **
 
    // calculate the two eigenvalues closest to 0.0, using shift and invert method
    eigensolver::EasyArPackppStd<concepts::Cmplx, concepts::Real> eacs(A, 2, 0.0);
    concepts::Array<concepts::Cmplx> eigenvalues = eacs.getSolver()->getEV();
 
    // get the corresponding eigenvectors
    concepts::Array<concepts::Vector<concepts::Cmplx> *> eigenvectors = eacs.getSolver()->getEF();
 
    // vectors to tests the solutions
    concepts::Vector<concepts::Cmplx> res1(eigenvectors[0]->size());
    concepts::Vector<concepts::Cmplx> res2(eigenvectors[0]->size());
 
    // test accuracy of the solution and show calculated eigenvalue
    res1 = *eigenvectors[1];
    A(res1, res2);
    std::cout << "First residuum: " << ((res1 * eigenvalues[1]) - res2).l2() << std::endl;
    std::cout << "Eigenvalue with smallest distance to 0.0: " << eigenvalues[1] << std::endl;
 
    // calculate the two eigenvalues with largest magnitude using regular mode
    eigensolver::EasyArPackppStd<concepts::Cmplx, concepts::Real> eacs2(A, 2, (char*) "LM");
    eigenvalues = eacs2.getSolver()->getEV();
    eigenvectors = eacs2.getSolver()->getEF();
 
    // test accuracy of the solution and show calculated eigenvalue
    res1 = *eigenvectors[1];
    A(res1, res2);
    std::cout << "Second residuum: " << ((res1 * eigenvalues[1]) - res2).l2() << std::endl;
    std::cout << "Eigenvalue with largest magnitude:  " << eigenvalues[1] << std::endl;
 
        
    // ** use EasyArpackppGen to solve general eigenproblems **
 
    // calculate the two eigenvalues closest to 0.0, using shift and invert method
    eigensolver::EasyArPackppGen<concepts::Cmplx, concepts::Real> eacg(A, B, 2, 0.0);
    eigenvalues = eacg.getSolver()->getEV();
    eigenvectors = eacg.getSolver()->getEF();
    
    // test accuracy of the solution and show calculated eigenvalue
    A((*eigenvectors[1]), res1);
    B((*eigenvectors[1]), res2);
    std::cout << "Third residuum: " << (res1 - (res2 * eigenvalues[1])).l2() << std::endl;
    std::cout << "Eigenvalue with smallest distance to 0.0: " << eigenvalues[1] << std::endl;
 
    // calculate the two eigenvalues with largest magnitude, using regular mode
    eigensolver::EasyArPackppGen<concepts::Cmplx, concepts::Real> eacg2(A, B, 2, (char*) "LM");
    eigenvalues = eacg2.getSolver()->getEV();
    eigenvectors = eacg2.getSolver()->getEF();
    
    // test accuracy of the solution and show calculated eigenvalue
    A((*eigenvectors[1]), res1);
    B((*eigenvectors[1]), res2);
    std::cout << "Fourth residuum: " << (res1 - (res2 * eigenvalues[1])).l2() << std::endl;
    std::cout << "Eigenvalue with largest magnitude: " << eigenvalues[1] << std::endl;
 
        
    // ** use EasyArPackppSymGen to solve general, symmetric eigenproblems **
 
    // eigenvalues of the problem C x = lambda B x  calculated with Octave
    double eigenvalue1 = -0.1691925951083604;
    double eigenvalue2 =  0.0619419844415557;
    double eigenvalue3 =  0.3841300911212291;
 
    // use Cayley mode
    eigensolver::EasyArPackppSymGen easg1(C, B, 1, eigenvalue1);
    std::cout << "Difference of Octave solution and Arpack++ solution using Cayley mode: " 
        << (easg1.getSolver()->getEV())[0] - eigenvalue1 << std::endl;
 
    // use Buckling mode
    eigensolver::EasyArPackppSymGen easg2('B', C, B, 1, eigenvalue2);
    std::cout << "Difference of Octave solution and Arpack++ solution using Buckling mode: "
        << (easg2.getSolver()->getEV())[0] - eigenvalue2 << std::endl;
 
    // use standard shift and invert mode
    eigensolver::EasyArPackppSymGen easg3('S', C, B, 1, eigenvalue3);
    std::cout << "Difference of Octave solution and Arpack++ solution using shift and invert mode: "
        << (easg3.getSolver()->getEV())[0] - eigenvalue3 << std::endl;
 
  } catch (concepts::ExceptionBase& e) {
    std::cout << e << std::endl;
    return 1;
  }
 
#ifdef HAS_MPI
  MPI_Barrier(MPI_COMM_WORLD);
  MPI_Finalize();
#endif
 
}