


Next: Bibliography
Project:
Hybrid
Coupling
| Researcher(s) |
: |
Prof. Dr. R. Hiptmair |
| |
: |
Prof. Dr.
Ana Alonso-Rodriguez, Universita Degli Studi Di Trento, Ital, |
| |
: |
Prof. Dr.
Alberto Valli, Universita Degli Studi Di Trento, Italy |
| Funding |
: |
no external funding |
| Duration |
: |
ongoing project |
Description. The general principle
underlying hybrid coupling can best
be explained in the case the scalar model problem
for some 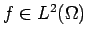 . This way to write the
boundary value
problem is
called the primal formulation. The corresponding dual
formulation
relies on the first order system
. This way to write the
boundary value
problem is
called the primal formulation. The corresponding dual
formulation
relies on the first order system
This is sometimes referred to as the mixed formulation of (1). Primal and dual
formulations give rise to different variational problems. It is the
gist of the hybrid coupling approach to employ these two variational
formulations
on different subdomains of a partition of the computational domain. An
important
restriction is that the same formulation must not be used on adjacent
sub-domains.
Let us assume that 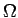 is partitioned into two
connected Lipschitz subdomains
is partitioned into two
connected Lipschitz subdomains
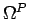 (``primal'') and
(``primal'') and
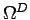 (``dual'') such that
(``dual'') such that
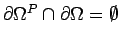 . Let
. Let 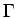 be their common
interface, with the unit normal
be their common
interface, with the unit normal 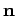 on
on 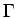 pointing into
pointing into
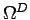 . On
. On
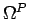 we resort to the primal
variational formulation obtained from
integration by parts applied to (1):
seek
we resort to the primal
variational formulation obtained from
integration by parts applied to (1):
seek
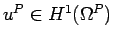 such that
such that
On 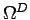 the
mixed variational formulation will be used, which emerges from
casting the first equation of (2)
into weak form and retaining the second
strongly: seek
the
mixed variational formulation will be used, which emerges from
casting the first equation of (2)
into weak form and retaining the second
strongly: seek 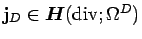 ,
,
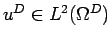 such
that
such
that
(remember that 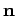 is the unit inward
normal vector on
is the unit inward
normal vector on 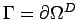 ).
).
Both problems can be linked by the transmission conditions
on 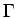 :
:
These can be used to express the interface terms in both (3) and (4) through quantities from
the other subdomain. Subsequently
merging the variational formulations we arrive at the final coupled
problem:
Let us denote by 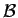 the bilinear form on
the bilinear form on 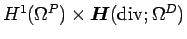 corresponding to the left-upper
corresponding to the left-upper 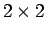 block of
(6). The crucial
observation is that
block of
(6). The crucial
observation is that 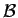 itself features a block-skew-symmetric
structure,
which involves
itself features a block-skew-symmetric
structure,
which involves
because the interface contributions cancel. This makes it possible to
show that 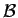 satisfies an inf-sup condition on
satisfies an inf-sup condition on 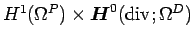 .
Beware, that this is not straightforward from (7), because the
one-dimensional topological
subspace of constants on
.
Beware, that this is not straightforward from (7), because the
one-dimensional topological
subspace of constants on 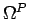 requires a
special treatment. Then the theory of saddle-point problems confirms
existence and
uniqueness of solutions of (7).
Moreover, Galerkin approximations by the
standard conforming finite element spaces for
requires a
special treatment. Then the theory of saddle-point problems confirms
existence and
uniqueness of solutions of (7).
Moreover, Galerkin approximations by the
standard conforming finite element spaces for 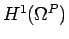 ,
,
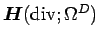 and
and 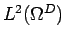 will enjoy optimality [WW98].
will enjoy optimality [WW98].
It is important to note that the coupling of the two subdomains in (7) is
purely variational, because none of the transmission conditions (5) shows
up in the definition of the spaces. This makes (7) attractive, if
unrelated (``non-matching'') finite element meshes are to be
used on
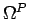 and
and
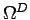 .
.
Hybrid coupling for eddy current problems. The eddy current
equations
in frequency domain
give rise to another example of a second order boudary value problem.
The hybrid
coupling idea outlined above can also be applied to this system, though
the theoretical analysis becomes more involved [AHV04,ARHV04].
The reason is
that 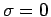 is encountered in non-conducting
regions.
is encountered in non-conducting
regions.
Hybrid domain decomposition on non-matching grids. We want to
resort to
the hybrid coupling idea to deal with non-matching grids arising from a
partitioning of 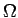 into subdomains
into subdomains
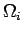 , across whose boundaries
the finite element meshes need not match
see Fig. 1.
, across whose boundaries
the finite element meshes need not match
see Fig. 1.
Figure 1:
Decomposition of 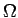
|
|
The idea is to introduce narrow stripes of width
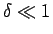 along the interfaces,
see Fig. 2. In these
stripes the problem is cast into primal form, whereas
in the remainder of the domain we use the mixed form. Letting width of
the stripes
tend to zero, we hope to obtain a mixed formulation on the non-matching
meshes.
along the interfaces,
see Fig. 2. In these
stripes the problem is cast into primal form, whereas
in the remainder of the domain we use the mixed form. Letting width of
the stripes
tend to zero, we hope to obtain a mixed formulation on the non-matching
meshes.
Figure 2:
Stripes along interfaces equipped with virtual meshes
|
|



Next: Bibliography
Prof. Ralf Hiptmair
2004-11-11
![]() is partitioned into two
connected Lipschitz subdomains
is partitioned into two
connected Lipschitz subdomains
![]() (``primal'') and
(``primal'') and
![]() (``dual'') such that
(``dual'') such that
![]() . Let
. Let ![]() be their common
interface, with the unit normal
be their common
interface, with the unit normal ![]() on
on ![]() pointing into
pointing into
![]() . On
. On
![]() we resort to the primal
variational formulation obtained from
integration by parts applied to (1):
seek
we resort to the primal
variational formulation obtained from
integration by parts applied to (1):
seek
![]() such that
such that
![]() :
:
![]() and
and
![]() .
.
![]() into subdomains
into subdomains
![]() , across whose boundaries
the finite element meshes need not match
see Fig. 1.
, across whose boundaries
the finite element meshes need not match
see Fig. 1.
![]() along the interfaces,
see Fig. 2. In these
stripes the problem is cast into primal form, whereas
in the remainder of the domain we use the mixed form. Letting width of
the stripes
tend to zero, we hope to obtain a mixed formulation on the non-matching
meshes.
along the interfaces,
see Fig. 2. In these
stripes the problem is cast into primal form, whereas
in the remainder of the domain we use the mixed form. Letting width of
the stripes
tend to zero, we hope to obtain a mixed formulation on the non-matching
meshes.