START Project "Geometry of Stochastic Differential Equations" by Josef Teichmann
The START Prize is awarded by the Austrian Science Fund (FWF) on behalf of the Federal Ministry for Education, Science and Culture (BM:BWK).
My START-project is called "Geometry of Stochastic Differential Equations". See also the START-Portal for details on this Start-project. This project and its research group will be located at FAM at Vienna University of Technology.
As often in science, a project is best explained by giving examples of problems, which I have in mind:
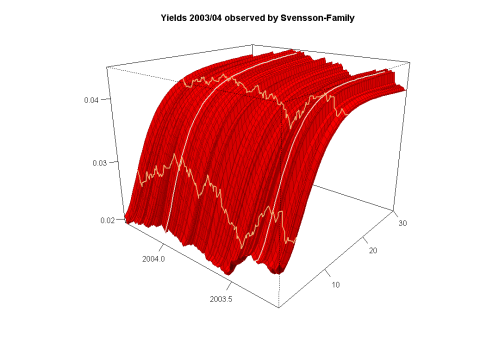
- In Interest Rate Theory, as in other areas of applied mathematics, one has to deal with unusual geometric tasks like the description of rough geometric objects. The following picture shows an interest rate evolution between 2003 and 2004: we see the change of the rates as rough direction (highlighted by the two vertical curves) and we see the rates for different times to maturity as smooth direction (please click on the graph for a bigger version).
- The analysis of such surfaces in a qualitative and quantitative way is one of the cornerstones of this project. The theory quickly leads to Stochastic Differential Equations with values in Hilbert spaces, the practical implementations lead to parametrized families of curves in order to fit the daily rates in banks or investment houses. Frobenius Theorem for unbounded vector fields, analysis of involutive bundles on Hilbert spaces are the link between the theoretical framework of SDEs and the practical need for finitely parametrized families of curves.
- We aim to deal with similar problems for Levy-driven SDEs and expect new and exciting geometric phenomena.
During our research we plan to investigate the following fields based upon several key publications. See my publications at the respective number.
FDR for Levy-driven Stochastic Differential Equations in infinite dimensions
[7] Damir Filipovic, Josef Teichmann: Existence of invariant Manifolds for Stochastic Equations in infinite dimension, Journal of Functional Analysis 197, 398-432, 2003.
[8] Josef Teichmann: A Frobenius Theorem on convenient manifolds, Monatshefte für Mathematik 134, 159-167, 2001.
[12] Friedrich Hubalek, Irene Klein, Josef Teichmann: A general proof of the Dybvig-Ingersoll-Ross-Theorem: Long forward rates can never fall, Mathematical Finance 12 (4), 447-451, 2002.
[13] Damir Filipovic, Josef Teichmann: Regularity of Finite-dimensional Realizations for Evolution Equations, Journal of Functional Analysis 197, 433-446, 2003.
[14] Damir Filipovic, Josef Teichmann: On the Geometry of the Term structure of Interest Rates, Proceedings of the Royal Society London A 460, 129-167, 2004.
Hypo-ellipticity in mathematical Finance
[15] Fabrice Baudoin, Josef Teichmann: Hypoellipticity in infinite dimensions and an application to interest rate theory, Annals of applied Probability 15 (3), 1765-1777, 2005.
Distributional Properties of Iterated Stratonovich Integrals
[19] Josef Teichmann: Calculating the Greeks by Cubature formulas, Proceedings of the Royal Society London A 462, 647-670, 2006.
Hedging in Finite Factor Models
[22] Barbara Forster, Eva Lütkebohmert, Josef Teichmann: Calculation of Greeks for Jump-Diffusions, submitted, 2006.
Numerical Probability Theory (Cubature Methods, Simulation of Iterated Stratonvich Integrals)
[19] Josef Teichmann: Calculating the Greeks by Cubature formulas, Proceedings of the Royal Society London A 462, 647-670, 2006.
Optimal Transportation
[23] Walter Schachermayer, Josef Teichmann: Characterization of optimal Transport Plans for the Monge-Kantorovich-Problem, Proceedings of the AMS, to appear, 2006.