-
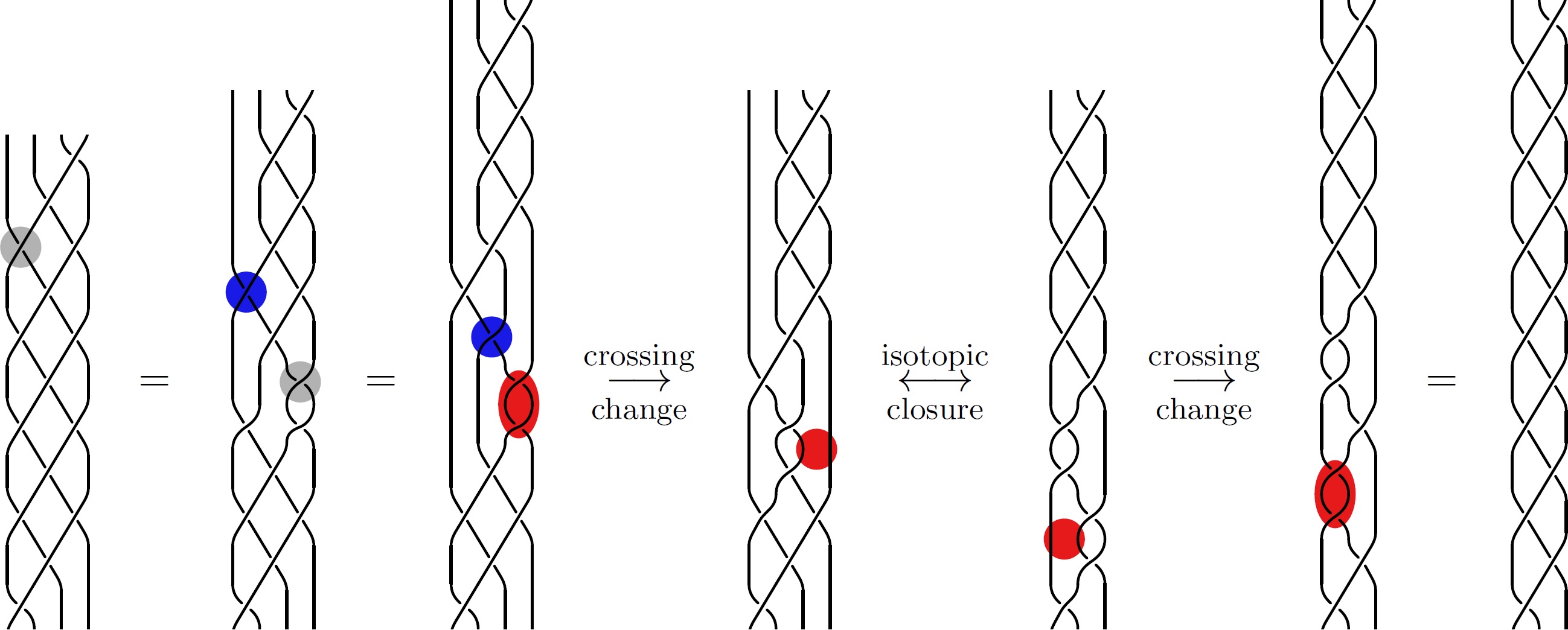
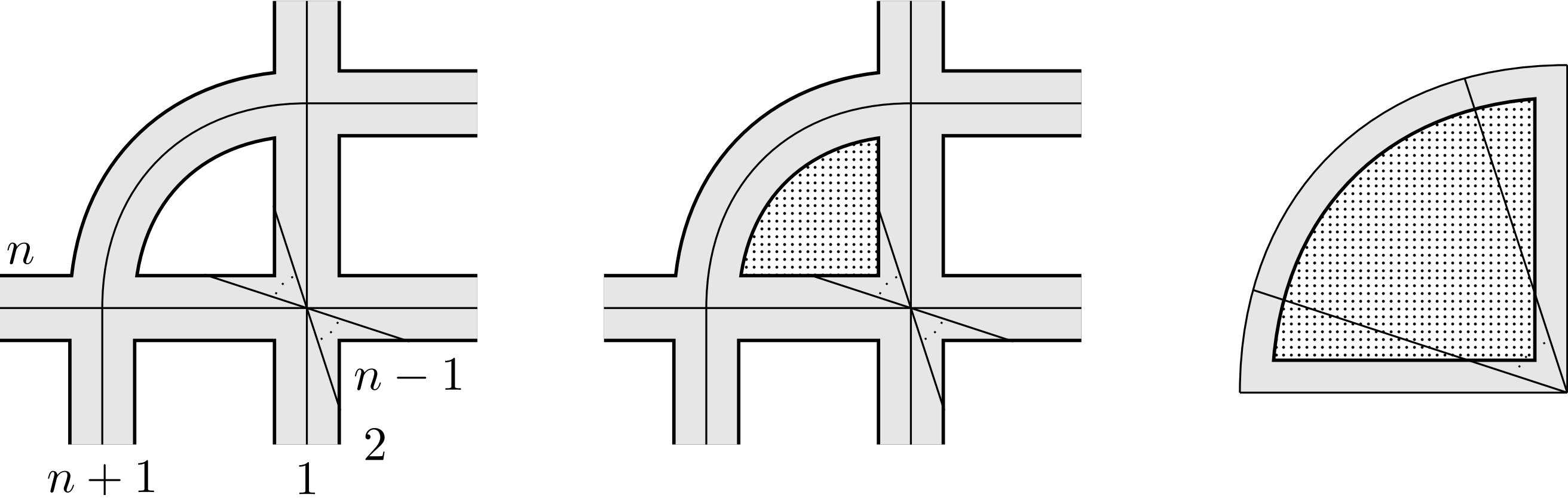
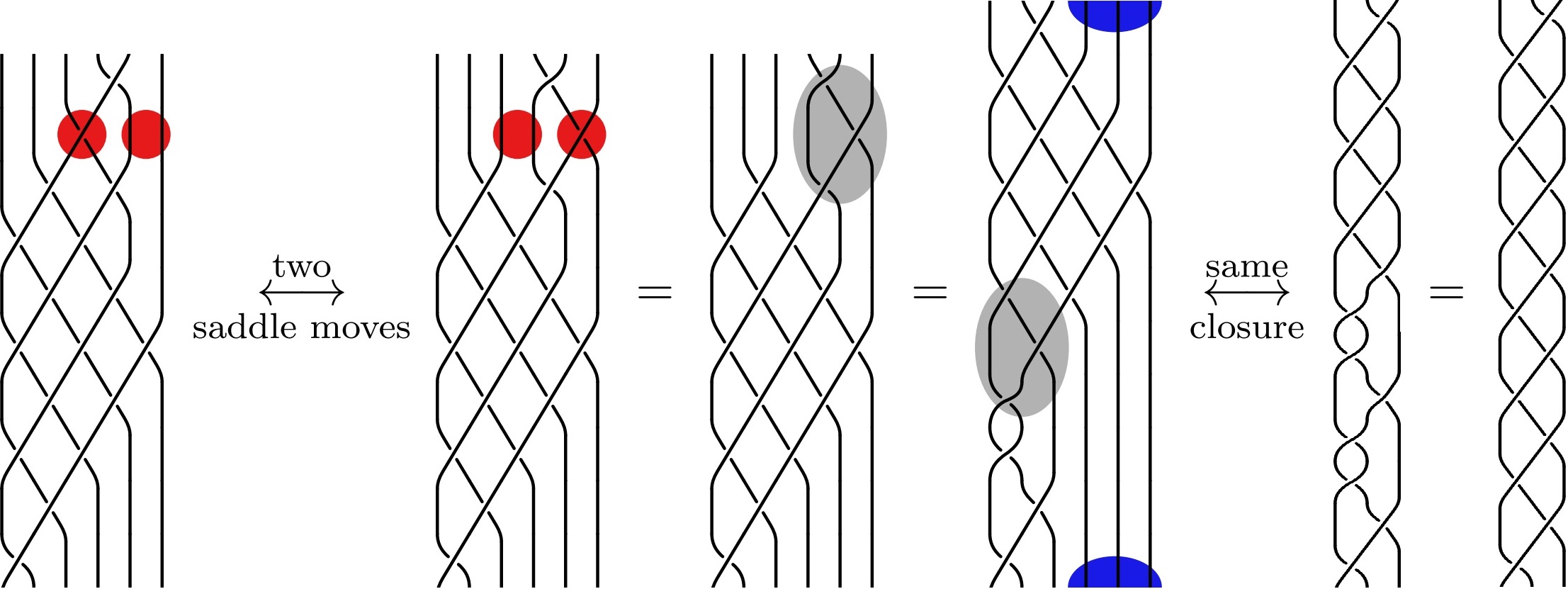
Homogeneous braids are visually prime. [ArXiv:2408.15730]
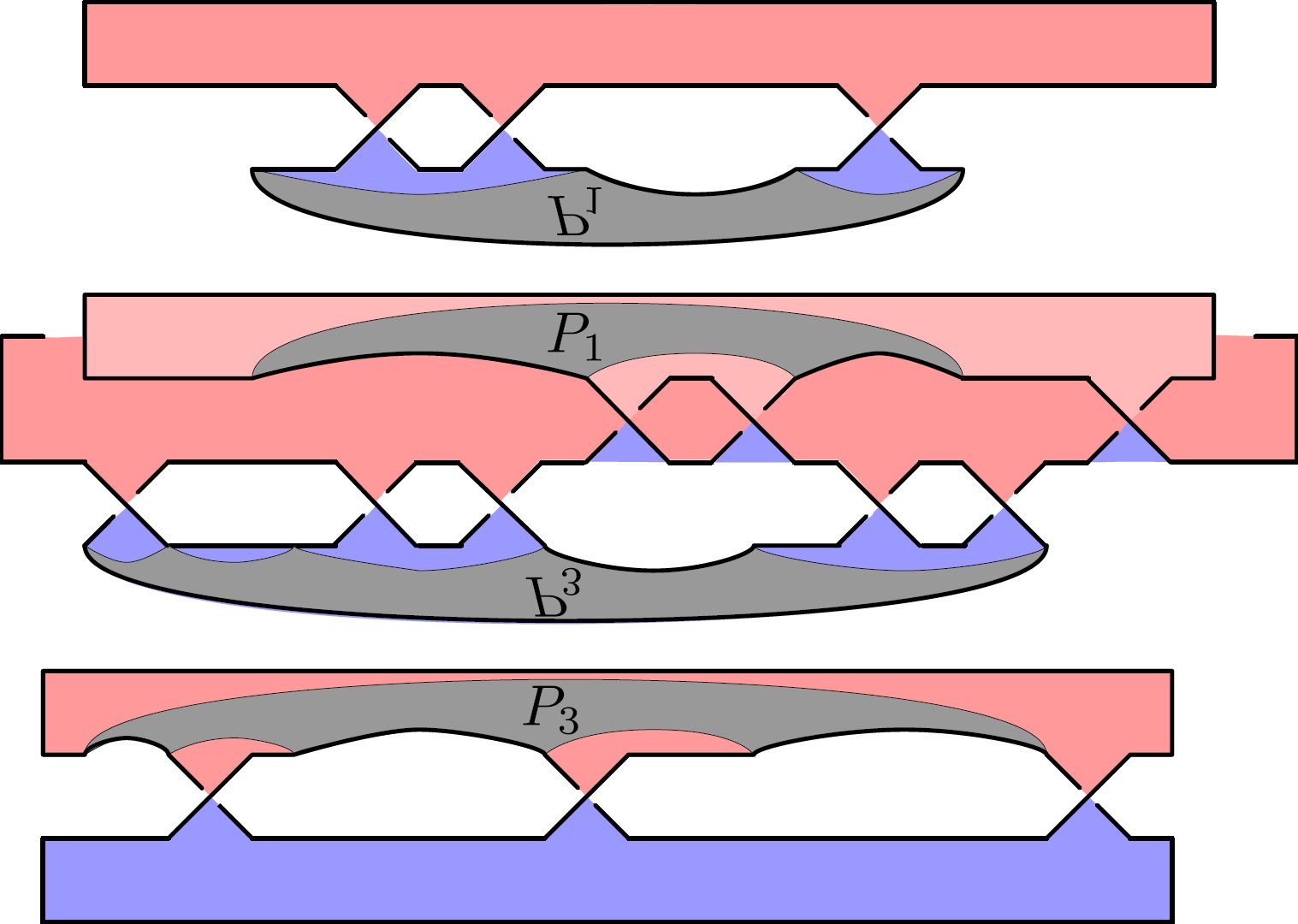
With Lukas Lewark and Miguel Orbegozo Rodriguez.Abstract: We show that closures of homogeneous braids are visually prime, addressing a question of Cromwell. The key technical tool for the proof is the following criterion concerning primeness of open books, which we consider to be of independent interest. For open books of 3-manifolds the property of having no fixed essential arcs is preserved under essential Murasugi sums with a strictly right-veering open book, if the plumbing region of the original open book veers to the left. We also provide examples of open books in S^3 demonstrating that primeness is not necessarily preserved under essential Murasugi sum, in fact not even under stabilizations a.k.a. Hopf plumbings. Furthermore, we find that trefoil plumbings need not preserve primeness. In contrast, we establish that figure-eight knot plumbings do preserve primeness.
-
Effective hyperbolization and length bounds for Heegaard splittings. [ArXiv:2408.06998]
With Alessandro Sisto and Gabriele Viaggi.Abstract: We consider 3-manifolds M given as Heegaard splittings with the aim to describe the hyperbolic metric of M under topological conditions on the splitting guaranteeing that the manifold is hyperbolic. In particular, given a suitable "sufficiently incompressible" curve γ in a Heegaard surface Σ for M, we show (without appealing to Geometrization) that M is hyperbolic and we compute the length of γ in terms of the projection coefficients of the disk sets, up to a uniform multiplicative error.
-
The twisting number of a ribbon knot is bounded below by its doubly slice genus. [ArXiv:2404.07619]
With Vitalijs Brejevs.Abstract: The twisting number of a ribbon knot K is the minimal number of tangle replacements on the symmetry axis of J#-J for any knot J that is required to produce a symmetric union diagram of K. We prove that the twisting number is bounded below by the doubly slice genus and produce examples of ribbon knots with arbitrarily high twisting number, addressing a problem of Tanaka. To this end, we establish a result of independent interest that the doubly slice genus of K is bounded above by the oriented band move distance between K and any weakly doubly slice link, which also enables us to determine hitherto unknown doubly slice genera of some knots with 12 crossings.
-
Seifert surfaces in the four-ball and composition of binary quadratic forms. [ArXiv:2311.17746]
With Menny Aka, Alison B. Miller, and Andreas Wieser.Abstract: We use composition of binary quadratic forms to systematically create pairs of Seifert surfaces that are non-isotopic in the four-ball. Our main topological result employs Gauss composition to classify the pairs of binary quadratic forms that arise as the Seifert forms of pairs of disjoint Seifert surfaces of genus one. The main ingredient of the proof is number-theoretic and of independent interest. It establishes a new connection between the Bhargava cube and the geometric approach to Gauss composition via planes in the space of two-by-two matrices. In particular, we obtain a geometric recipe that given any two binary quadratic forms finds the Bhargava cube that gives rise to their composition.
-
The Dehn twist coefficient for big and small mapping class groups. [ArXiv:2308.06214]
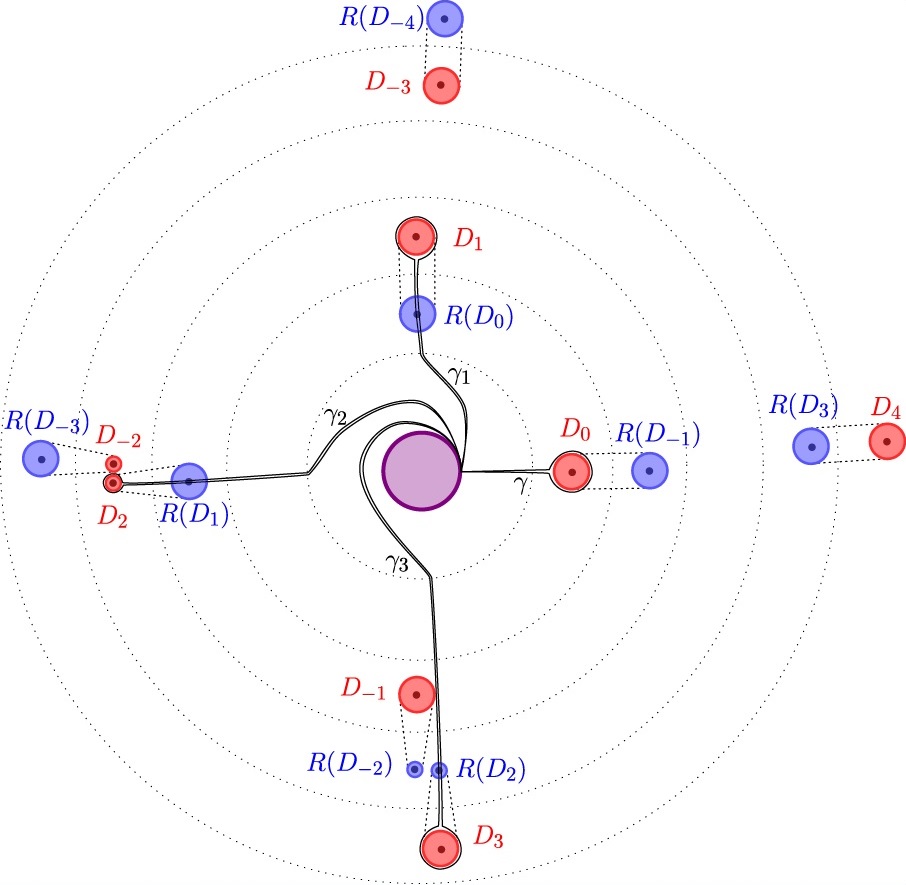
With Diana Hubbard and Hannah Turner.Abstract: We study a quasimorphism, which we call the Dehn twist coefficient (DTC), from the mapping class group of a surface (with a chosen compact boundary component) that generalizes the well-studied fractional Dehn twist coefficient (FDTC) to surfaces of infinite type. Indeed, for surfaces of finite type the DTC coincides with the FDTC. We provide a characterization of the DTC (and thus also of the FDTC) as the unique homogeneous quasimorphism satisfying certain positivity conditions. The FDTC has image contained in the rational numbers. In contrast to this, we find that for some surfaces of infinite type the DTC has image all of the real numbers. To see this we provide a new construction of maps with irrational rotation behavior for some surfaces of infinite type with a countable space of ends or even just one end. In fact, we find that the DTC is the right tool to detect irrational rotation behavior, even for surfaces without boundary.
New example of mapping classes with irrational rotation behavior. For many surfaces of infinite type, we provide new examples of mapping classes, one for each irrational number λ such that its DTC is λ, that we call wagon wheel maps. The picture to the right (when correctly decoded) explains the construction. -
Hyperbolic Heegaard splittings and Dehn twists. [ArXiv:2304.05990]
With Alessandro Sisto and Gabriele Viaggi.Abstract: We consider the family of Heegaard splittings of genus g at least three which are defined via a glueing map that is the n-th power of the Dehn twist along a curve that satisfies a natural topological assumption, namely pared acylindricity. We show that if n is at least 14, then the Heegaard splitting has a hyperbolic metric for which the simple closed curve defining the Dehn twist is a closed geodesic of length at least 0.7/(n^2g^2) and at most 34.3/n^2.
-
Asymptotics of the smooth An-realization problem. [ArXiv:2303.15434]
With Sebastian Baader.Abstract: We solve an asymptotic variant of a smooth version of the An-realization problem for plane curves. As an application, we determine the cobordism distance between torus links of type T(d,d) and T(2,N) up to an error of at most 3d. We also discuss the limits of knot theoretic approaches aimed at solving the An-realization problem.
-
The slice-Bennequin inequality for the fractional Dehn twist coefficient. [ArXiv:2204.05288], accepted for publication in J. Inst. Math. Jussieu
Abstract: We characterize the fractional Dehn twist coefficient (FDTC) on the n-stranded braid group as the unique homogeneous quasimorphism to the real numbers of defect at most 1 that equals 1 on the positive full twist and vanishes on the (n-1)-stranded braid subgroup. In a different direction, we establish that the slice-Bennequin inequality holds with the FDTC in place of the writhe. In other words, we establish an affine linear lower bound for the smooth slice genus of the closure of a braid in terms of the braid's FDTC. We also discuss connections between these two seemingly unrelated results. In the appendix we provide a unifying framework for the slice-Bennequin inequality and its counterpart for the FDTC.
-
On the values taken by slice torus invariants. [ArXiv:2202.13818], accepted for publication in Proc. Cambridge Philos. Soc.
With Lukas Lewark and Andrew Lobb.Abstract: We study the space of slice torus invariants. In particular we characterize the set of values that slice torus invariants may take on a given knot in terms of the stable smooth slice genus. Our study reveals that the resolution of the local Thom conjecture implies the existence of slice torus invariants without having to appeal to any explicit construction from a knot homology theory.
-
Squeezed knots.
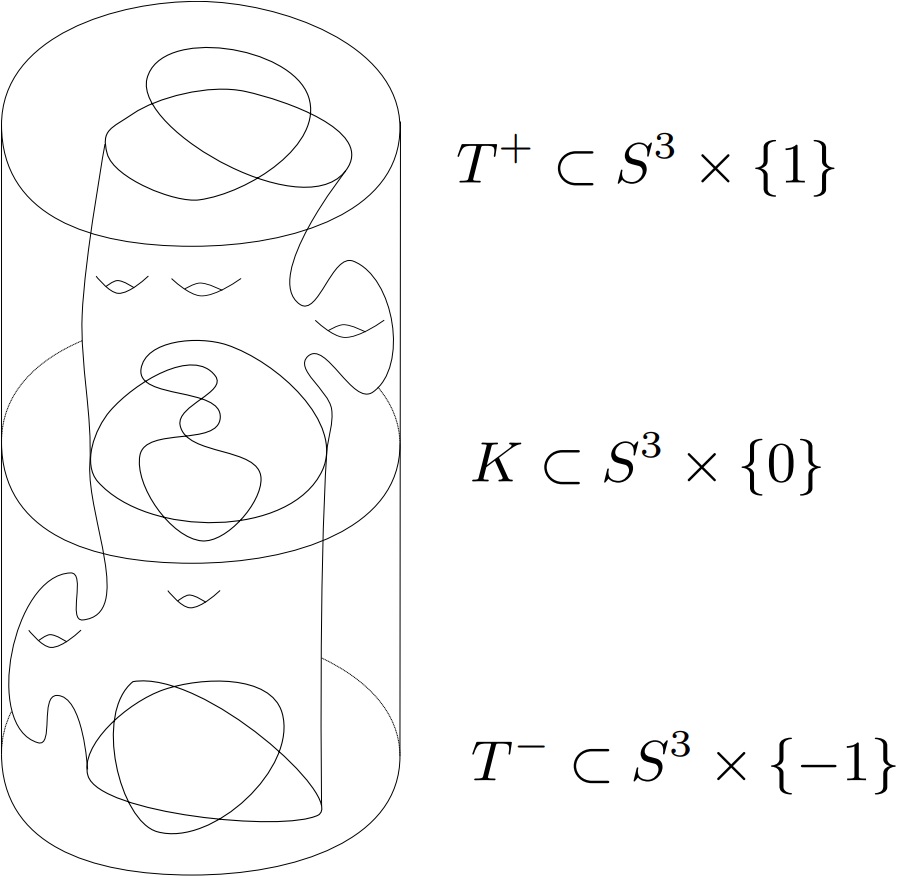 [ArXiv:2202.12289], accepted for publication in Quantum Topol.
[ArXiv:2202.12289], accepted for publication in Quantum Topol.
With Lukas Lewark and Andrew Lobb.Abstract: Squeezed knots are those knots that appear as slices of genus-minimizing oriented smooth cobordisms between positive and negative torus knots (see figure for a schematic). We show that this class of knots is large and discuss how to obstruct squeezedness. The most effective obstructions appear to come from quantum knot invariants, notably including refinements of the Rasmussen invariant due to Lipshitz-Sarkar and Sarkar-Scaduto-Stoffregen involving stable cohomology operations on Khovanov homology.
Many knots are squeezed. The class of squeezed knots contains all knots that are positive, negative, quasipositive, quasinegative, alternating, homogeneous, alternative, or pseudoalternating. Also, it is closed under mirroring, orientation reversal, concordance, and connected summing.
Many concordance invariants behave predictably on squeezed knots. For example, slice torus invariants, like τ (Heegaard-Floer) and s/2 (Khovanov homology)), are all equal on squeezed knots (and the value can be read off from a cobordism that witnesses squeezedness).
So, if your favorite class of knots for which you can calculate a particular slice torus invariant turns out to be subsumed by squeezed knots, then in fact you have calculated all slice torus invariants on said class, and, maybe, your calculation can be understood as coming from a squeezing procedure.
 Avoid squeezed knots.
You invented a new invariant (maybe by cleverly exploiting your favorite brand of a knot homology theory)
and you are looking for examples on which it distinguishes itself from other invariants?
If your invariant is slice torus or it fits in the squeezing obstruction scheme we describe in this paper,
you should be aware of knots that are known to be squeezed, and stay away from those! Luckily,
Avoid squeezed knots.
You invented a new invariant (maybe by cleverly exploiting your favorite brand of a knot homology theory)
and you are looking for examples on which it distinguishes itself from other invariants?
If your invariant is slice torus or it fits in the squeezing obstruction scheme we describe in this paper,
you should be aware of knots that are known to be squeezed, and stay away from those! Luckily,
Most knots should not be squeezed. While many classes of knots and most knots on (small) knot tables are squeezed, e.g. all but at most 6 prime knots with 10 or less crossings are squeezed, a generic knot (where generic is made precise in your favourite way) ought to be not squeezed. In particular, we believe that the quotient of the smooth concordance group by the subgroup of squeezed knots is very large. Maybe the invariant you invented could be used to make this precise ... let us know. Or it could be used to answer the following.
Are 10130 and 10141 squeezed? These are the first knots on the knot table for which we do not know the squeezing status. -
The ℤ-genus of boundary links. [ArXiv:2012.14367], accepted for publication in Rev. Mat. Complut.
With JungHwan Park and Mark Powell.Abstract: The ℤ-genus of a link L in S^3 is the minimal genus of a locally flat, embedded, connected surface in D^4 whose boundary is L and with the fundamental group of the complement infinite cyclic. We characterise the ℤ-genus of boundary links in terms of their single variable Alexander module, and we present some applications. In particular, we show that a variant of the shake genus of a knot, the ℤ-shake genus, equals the ℤ-genus of the knot.
-
Examples of non-minimal open books with high fractional Dehn twist coefficient. [ArXiv:2010.07869], accepted for publication in New York J. Math.
With Diana Hubbard.Abstract: In this short note we construct examples of open books for 3-manifolds that show that arbitrarily high twisting of the monodromy of the open book does not guarantee maximality of the Euler characteristic of the pages among the open books supporting the same contact manifold. We find our examples of open books as the double branched covers of families of closed braids studied by Malyutin and Netsvetaev.
-
A note on the four-dimensional clasp number of knots.
 [ArXiv:2009.01815], accepted for publication in Math. Proc. Cambridge Philos. Soc.
[ArXiv:2009.01815], accepted for publication in Math. Proc. Cambridge Philos. Soc.
With JungHwan Park.Abstract: Among the knots that are the connected sum of two torus knots with cobordism distance 1, we characterize those that have 4-dimensional clasp number at least 2, and we show that their n-fold connected self-sum has 4-dimensional clasp number at least 2n. Our proof works in the topological category. To contrast this, we build a family of topologically slice knots for which the n-fold connected self-sum has 4-ball genus n and 4-dimensional clasp number at least 2n.
-
Existence of Embeddings of Smooth Varieties into Linear Algebraic Groups. [ArXiv:2007.16164] [J. Algebraic Geom.]
With Immanuel van Santen.Abstract: We prove that every smooth affine variety of dimension d embeds into every simple algebraic group of dimension at least 2d+2. For this we employ and build upon parametric transversality results for flexible affine varieties established by Kaliman yielding a certain embedding method. We show that our result is optimal up to a possible improvement by one to 2d+1 by adapting a Chow-group based argument due to Bloch, Murthy, and Szpiro.
In order to study the limits of our embedding method, we also show that there do not exist proper dominant maps from the d-dimensional affine space to any d-dimensional homogeneous space of a simple algebraic group. The latter is proved using a version of Hopf's theorem on the Umkehrungshomomorphismus from algebraic topology and rational homology group calculations.
Projecting down to ℂ2d+1 à la Whitney: A smooth complex algebraic variety Z of dimension d, by definition a zero set of polynomials in complex affine space Cm, always embedds in ℂ2d+1 by the Holme-Kaliman-Srinivas theorem. Both the statement and the proof are inspired by Whitney's weak embedding theorem in smooth manifold theory. Very briefly, the Holme-Kaliman-Srinivas theorem is proven by projecting Z from ℂm to ℂ2d+1 using a generic linear map from ℂm to ℂ2d+1 and checking that such a map restricts to a proper injective immersion (ie an embedding) on Z. It seems unclear how this proof can be ported to other target varieties such as linear algebraic groups.
Building up to ℂ2d+1: The Holme-Kaliman-Srinivas theorem can also be obtained using a different method of proof. One starts with a fixed finite map n from Z to ℂd (finite ⇔ proper and points have finite preimage) and considers maps f from Z to ℂ2d+1 such that π∘f=n, where π denotes a fixed projection from ℂ2d+1 to ℂd. Given such an f, we quantify how much f fails to be an embedding (f is proper, but might fail to be injective and immersive) using the dimension of the points that map non-injectively under f and the maximal dimension of the kernels of the differentials of f. It turns out that one can iteratively improve f to an embedding (ie reduce the aforementioned dimensions to -∞ and 0, respectively) using certain transitivity properties of automorphisms of ℂ2d+1 that fix the fibers of the projection π.
Building up to other varieties: We consider more general varieties X of dimension 2d+1 that also have projection-like maps π: X→Cd such that certain transitivity properties for automorphism of X that fix the fibers of π hold. We show that under favourable conditions one finds f from Z to X with π∘f=n and one can also iteratively improve f to an embedding. We find our main result about algebraic groups by establishing that simple algebraic groups of dimension at least 2d+2 always have such (2d+1)-dimensional X as subvarieties. -
Bouquets of curves in surfaces.
 [ArXiv:2007.10429], accepted for publication in Glasg. Math. J.
[ArXiv:2007.10429], accepted for publication in Glasg. Math. J.
With Sebastian Baader and Levi Ryffel.Abstract: We characterise embedded bouquets of simple closed curves in orientable surfaces, in terms of relations between the corresponding Dehn twists.
-
Uniform models and short curves for random 3-manifolds.
 [ArXiv:1910.09486]
[ArXiv:1910.09486]
With Alessandro Sisto and Gabriele Viaggi.Abstract: We give two constructions of hyperbolic metrics on Heegaard splittings satisfying certain conditions that only use tools from the deformation theory of Kleinian groups. In particular, we do not rely on the solution of the Geometrization Conjecture by Perelman. Both constructions apply to random Heegaard splitting with asymptotic probability 1. The first construction provides explicit uniform bilipschitz models for the hyperbolic metric. The second one gives a general criterion for a curve on a Heegaard surface to be a short geodesic for the hyperbolic structure, such curves are abundant in a random setting. As an application of the model metrics, we discuss the coarse growth rate of geometric invariants, such as diameter and injectivity radius, and questions about arithmeticity and commensurability in families of random 3-manifolds.
-
Embedding spheres in knot traces.
 [ArXiv:2004.04204]
[Compos. Math.]
[ArXiv:2004.04204]
[Compos. Math.]
With Allison N. Miller, Matthias Nagel, Patrick Orson, Mark Powell, and Arunima Ray.Abstract: The trace of n-framed surgery on a knot in S^3 is a 4-manifold homotopy equivalent to the 2-sphere. We characterise when a generator of the second homotopy group of such a manifold can be realised by a locally flat embedded 2-sphere whose complement has abelian fundamental group. Our characterisation is in terms of classical and computable 3-dimensional knot invariants. For each n, this provides conditions that imply a knot is topologically n-shake slice, directly analogous to the result of Freedman and Quinn that a knot with trivial Alexander polynomial is topologically slice.
-
Non-orientable slice surfaces and inscribed rectangles.
.jpg) [ArXiv:2003.01590], accepted for publication in Ann. Sc. Norm. Super. Pisa Cl. Sci.
[ArXiv:2003.01590], accepted for publication in Ann. Sc. Norm. Super. Pisa Cl. Sci.
With Marco Golla.Abstract: We discuss differences between genera of smooth and locally-flat non-orientable surfaces in the 4-ball with boundary a given torus knot or 2-bridge knot. In particular, we establish that a result by Batson on the smooth non-orientable 4-genus of torus knots does not hold in the locally-flat category. We further show that certain families of torus knots are not the boundary of an embedded Möbius band in the 4-ball and other 4-manifolds.
Our investigation of non-orientable surfaces with boundary a given torus knot is motivated by our approach to unify the proof of the existence of inscribed squares and of inscribed rectangles with aspect ratio √3 in Jordan curves with a regularity condition. This generalizes a result by Hugelmeyer for smooth Jordan curves.
A locally-flat version of Hugelmeyer's reduction to knot concordance: The existence of certain inscribed rectangles in smooth Jordan curves follows from certain torus knots not bounding smooth Möbius bands in 4-space. Analyzing this argument of Hugelmeyer, it turns out that, for arbitrary Jordan curves, the existence of inscribed rectangles reduces to establishing that certain knots (or links) do not bound locally-flat Möbius bands (with punctures and union annuli in the case of links). We only manage to analyze the links that appear in special cases (in the text we consider Jordan curves that are locally graphs of 1-Lipschitz functions), but our dream is to treat arbitrary Jordan curves using locally-flat concordance theory. -
Genus one cobordisms between torus knots.
 [ArXiv:1910.01672]
[Int. Math. Res. Not.]
[ArXiv:1910.01672]
[Int. Math. Res. Not.]
With JungHwan Park.Abstract: We determine the pairs of torus knots that have a genus one cobordism between them, with one notable exception. This is done by combining obstructions using ν+ from the Heegaard Floer knot complex and explicit constructions of cobordisms. As an application, we determine the pairs of torus knots related by a single crossing change. Also, we determine the pairs of Thurston-Bennequin number maximizing Legendrian torus knots that have a genus one exact Lagrangian cobordism, with one exception.
-
A note on the topological slice genus of satellite knots. [ArXiv:1908.03760] [Algebr. Geom. Topol.]
With Allison N. Miller and Juanita Pinzon-Caicedo.Abstract: This paper presents evidence supporting the surprising conjecture that in the topological category the slice genus of a satellite knot P(K) is bounded above by the sum of the slice genera of K and P(U). Our main result establishes this conjecture for a variant of the topological slice genus, the ℤ-slice genus. As an application, we show that the (n,1)-cable of any 3-genus 1 knot (e.g. the figure 8 or trefoil knot) has topological slice genus at most 1. Further, we show that the lower bounds on the slice genus coming from the Tristram-Levine and Casson-Gordon signatures cannot be used to disprove the conjecture. Notably, the conjectured upper bound does not involve the algebraic winding number of the pattern P. This stands in stark contrast with the smooth category, where for example there are many genus 1 knots whose (n,1)-cables have arbitrarily large smooth 4-genera.
-
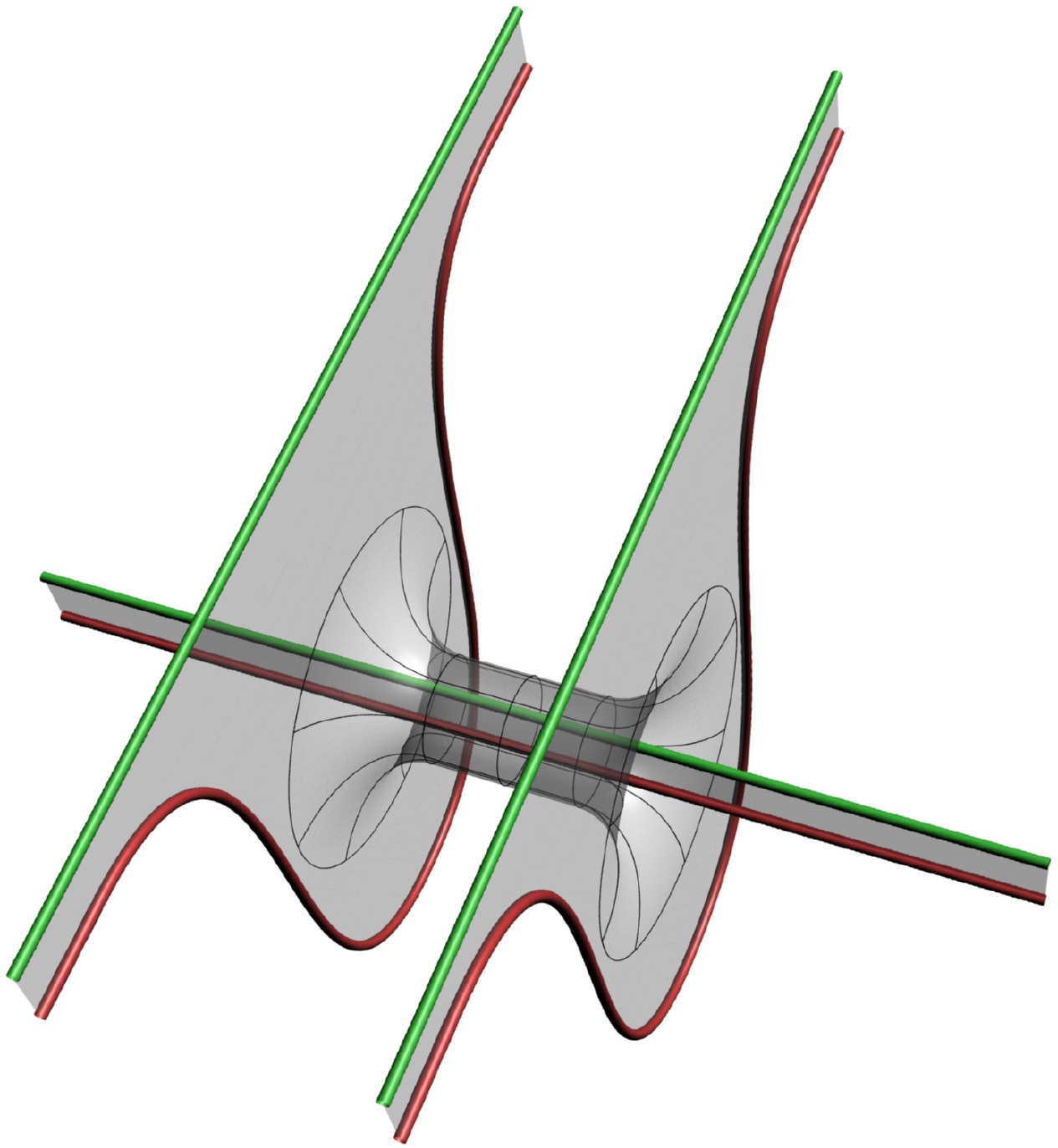 Balanced algebraic unknotting, linking forms, and surfaces in three- and four-space.
[ArXiv:1905.08305], accepted for publication in J. Differential Geom.
Balanced algebraic unknotting, linking forms, and surfaces in three- and four-space.
[ArXiv:1905.08305], accepted for publication in J. Differential Geom.
With Lukas Lewark.Abstract: We provide three 3-dimensional characterizations of the ℤ-slice genus of a knot, the minimum genus of a locally-flat surface in 4-space cobounding the knot whose complement has cyclic fundamental group: in terms of balanced algebraic unknotting, in terms of Seifert surfaces, and in terms of presentation matrices of the Blanchfield pairing. Using the latter characterization, we obtain effective lower bounds for the ℤ-slice genus from the linking pairing of the double branched cover of the knot. In contrast, we show that for odd primes p, the linking pairing on the first homology of the p-fold branched cover is determined up to isometry by the action of the deck transformation group on said first homology.
-
Almost positive links are strongly quasipositive. [ArXiv:1809.06692] [Math. Ann.]
With Lukas Lewark and Andrew Lobb.Abstract: We prove that a link is strongly quasipositive if it admits a diagram with a single negative crossing. This answers a question of Stoimenow's in the (strong) positive. As a second main result, we give simple and complete characterizations of link diagrams with quasipositive Seifert surfaces produced by Seifert's algorithm.
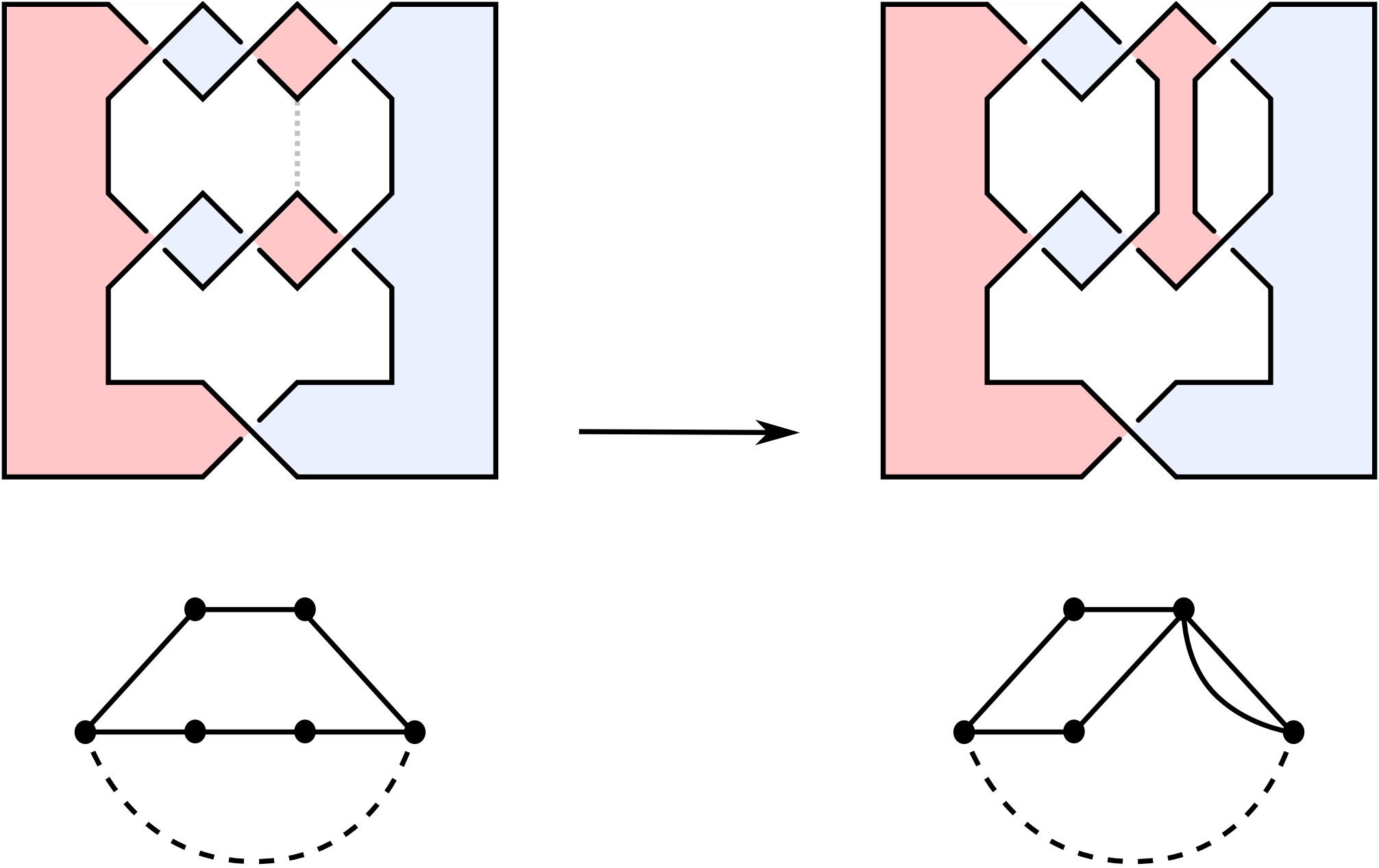 Approach via surfaces rather than diagrams:
We focus on canonical surfaces associated with link diagrams. We perform simplifying operations on diagrams
that change the link type(!),
but change the canonical surfaces in a `controlled' way.
Explicitly, we control quasipositivity of Seifert surfaces by relying on its behaviour under Murasugi summing and
taking incompressible surfaces.
`Merging of Seifert circles' (depicted) is one such simplifying operation:
it reduces the number of Seifert circles (aka vertices in the Seifert graph).
Approach via surfaces rather than diagrams:
We focus on canonical surfaces associated with link diagrams. We perform simplifying operations on diagrams
that change the link type(!),
but change the canonical surfaces in a `controlled' way.
Explicitly, we control quasipositivity of Seifert surfaces by relying on its behaviour under Murasugi summing and
taking incompressible surfaces.
`Merging of Seifert circles' (depicted) is one such simplifying operation:
it reduces the number of Seifert circles (aka vertices in the Seifert graph).
For the proof of the title theorem, this approach is in contrast to a `direct diagrammatical' approach of turning (through link isotopies) a given almost positive diagram into a standard diagram of a strongly quasipositive link.
Combinatorics of plane graphs: For our second main result, we use simplifying operations (e.g. merging of Seifert circles) and the existence of a canonical embedding of the Seifert graph for the relevant link diagrams into the plane (depicted), to reduce to a purely combinatorial problem about bipartite plane graphs. -
Up to topological concordance links are strongly quasipositive. [ArXiv:1802.02493] [J. Math. Pures Appl.]
With Maciej Borodzik.Abstract: We generalize an algorithm of Rudolph to establish that every link is topologically concordant to a strongly quasipositive link.
Context: Quasipositive links arise in the study of complex plane curves and their study is natural in the context of smooth concordance. In fact, results about complex curves (like the Thom conjecture proven by Kronheimer and Mrowka) places strong restrictions on the smooth concordance classes of links that contain quasipositive links. In contrast, our result establishes that quasipositive links are non-distinguishable from other links through the lens of topological concordance.
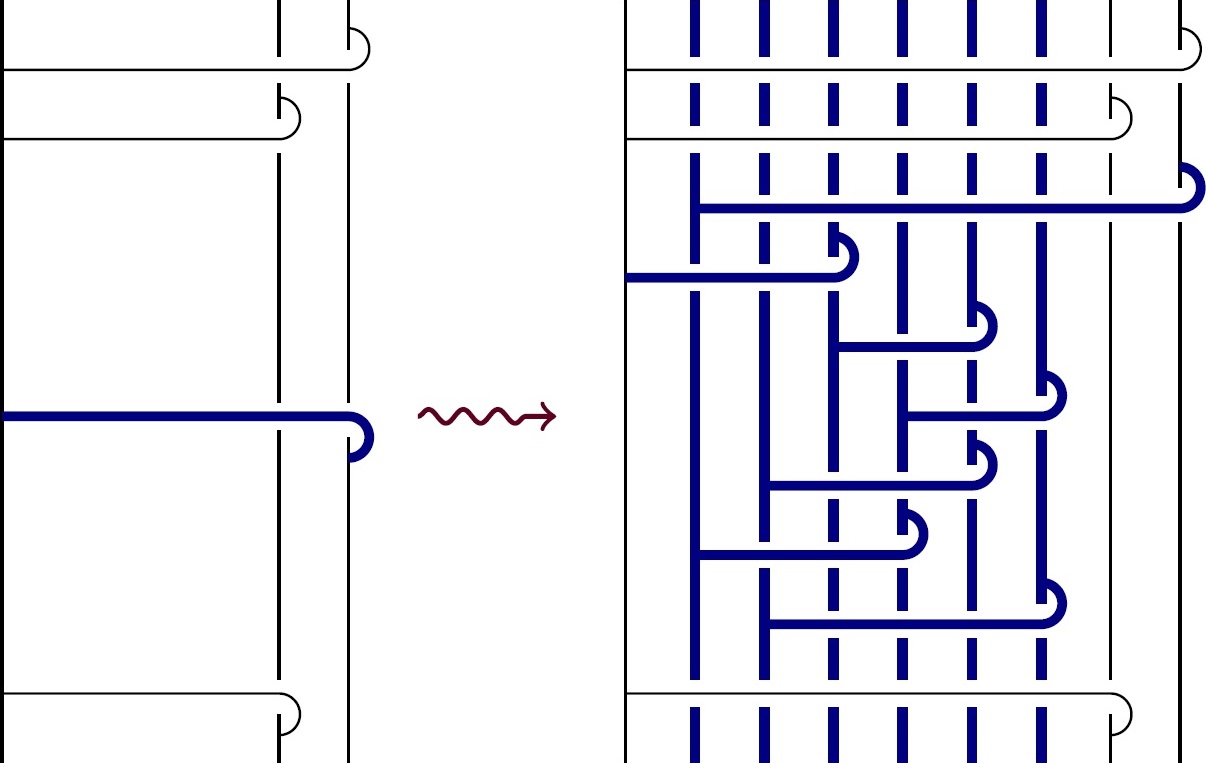 The proof:
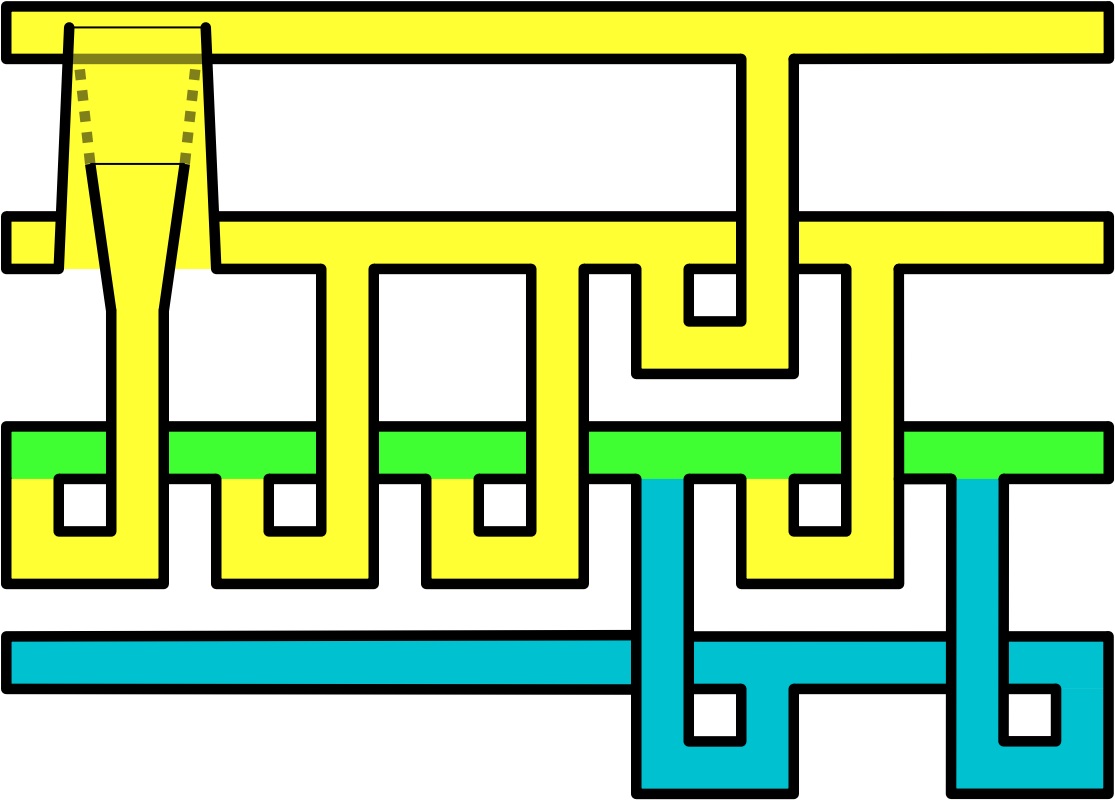
For the proof, we start with a link L, realize it as the boundary of a Seifert surface,
which we isotoped to consist of vertical disks and hooked horizontal bands (`hooks') (Figure).
Using that a Seifert surface is quasipositive (qp) if all hooks `go up',
we iteratively apply a 3D construction to turn the Seifert surface into a qp Seifert surface (in particular, its boundary is a strongly quasipositive link by definition).
Finally, we apply the disk embedding theorem to observe that the boundary of the resulting qp Seifert surface is topologically concordant to L.
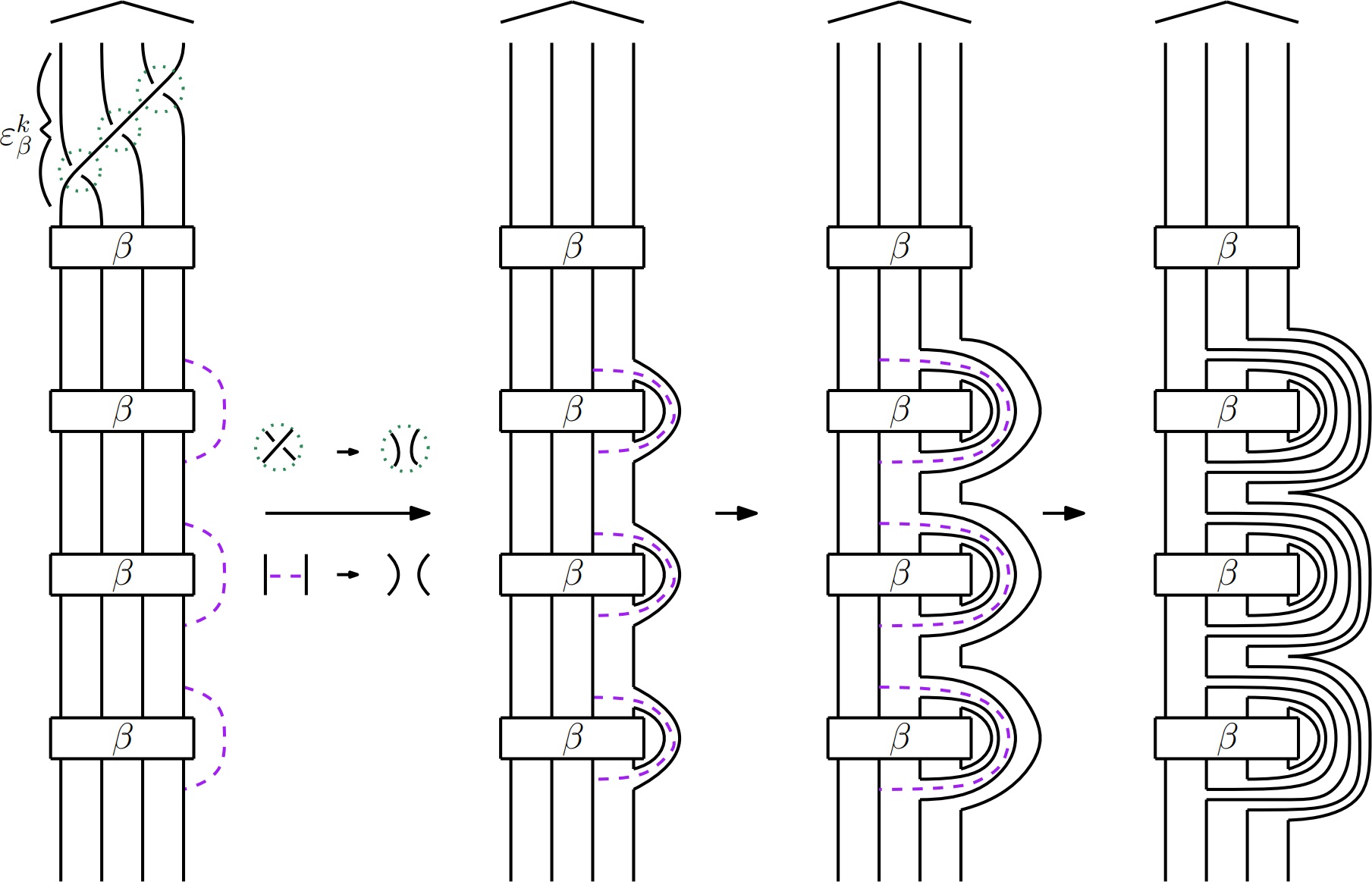
The proof:
For the proof, we start with a link L, realize it as the boundary of a Seifert surface,
which we isotoped to consist of vertical disks and hooked horizontal bands (`hooks') (Figure).
Using that a Seifert surface is quasipositive (qp) if all hooks `go up',
we iteratively apply a 3D construction to turn the Seifert surface into a qp Seifert surface (in particular, its boundary is a strongly quasipositive link by definition).
Finally, we apply the disk embedding theorem to observe that the boundary of the resulting qp Seifert surface is topologically concordant to L.
3D construction: Tying a zero-framed non-trivial knot that is strongly quasipositive into a hook that goes down results in a Seifert surface that can be represented with one less hook that goes down (Figure). The novelty here is that this can be done with every(!) non-trivial strongly quasipositive knot; previously, Rudolph had done this with the right-handed trefoil to realize all Seifert forms among qp Seifert surfaces.
4D punch line: Restricting the knots that are tied into the hooks to non-trivial strongly quasipositive knots with Alexander polynomial 1 implies (using Freedman's disk embedding theorem) that the 3D construction preserves the topological concordance class of the boundary. -
Calculating the homology and intersection form of a 4-manifold from a trisection diagram. [ArXiv:1711.04762] [Proc. Natl. Acad. Sci. USA]
With Michael Klug, Trent Schirmer, and Drew Zemke.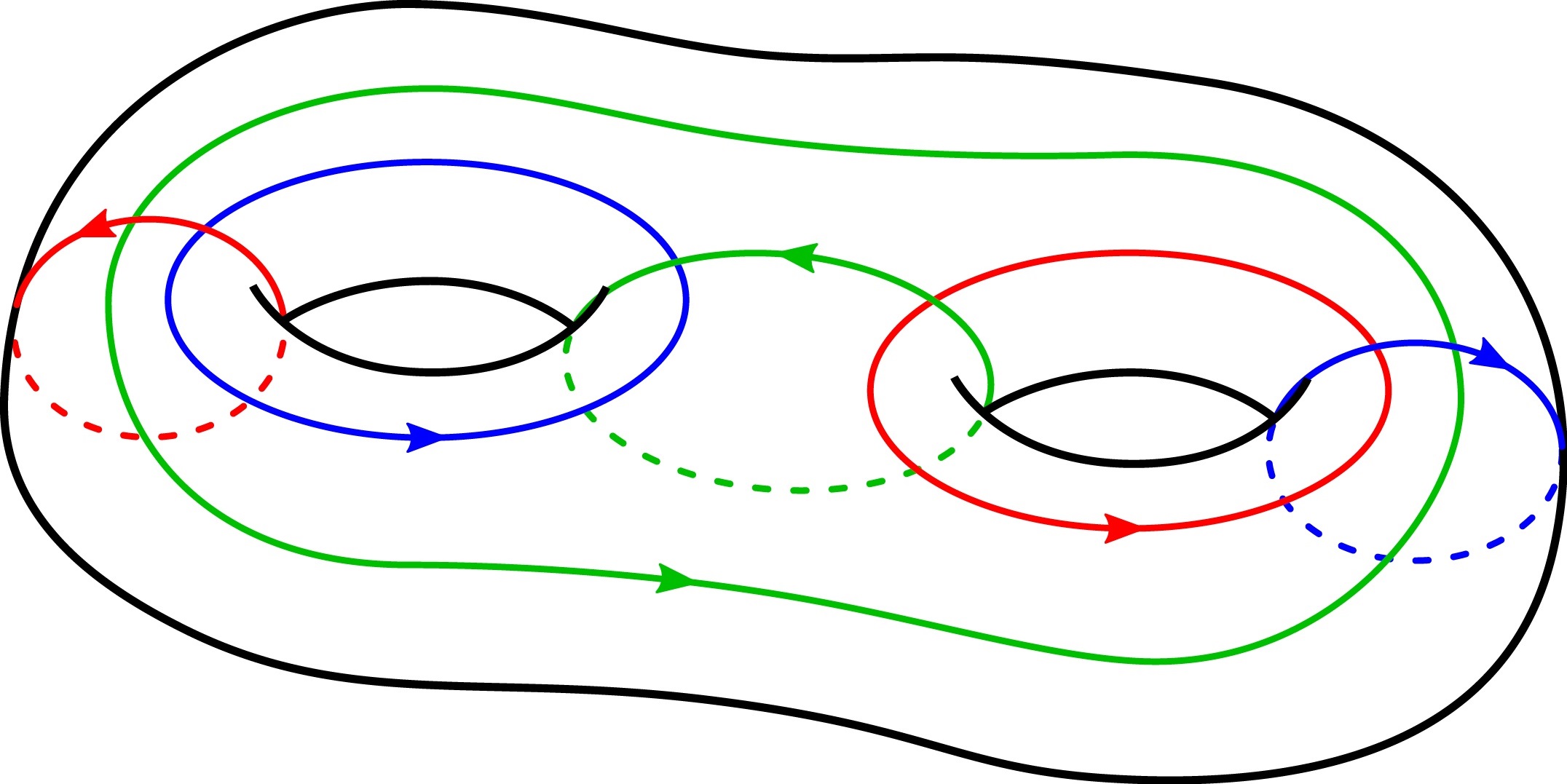
Abstract: Given a diagram for a trisection of a 4-manifold X, we describe the homology and the intersection form of X in terms of the three subgroups of the first homology of a diagram surface S for X. These three subgroups are generated by the three sets of curves and the intersection pairing on S. This includes explicit formulas for the second and third homology groups of X as well as an algorithm to compute the intersection form. Moreover, we show that all (g;k,0,0)-trisections admit "algebraically trivial" diagrams.
-
 Braids with as many full twists as strands realize the braid index.
[ArXiv:1708.04998]
[J. Topol.]
Braids with as many full twists as strands realize the braid index.
[ArXiv:1708.04998]
[J. Topol.]
With Diana Hubbard.Abstract: We characterize the fractional Dehn twist coefficient of a braid in terms of a slope of the homogenization of the Upsilon function, where Upsilon is the function-valued concordance homomorphism defined by Ozsváth, Stipsicz, and Szabó. We use this characterization to prove that n-braids with fractional Dehn twist coefficient larger than n-1 realize the braid index of their closure. As a consequence, we are able to prove a conjecture of Malyutin and Netsvetaev stating that n-times twisted braids realize the braid index of their closure. We provide examples that address the optimality of our results. The paper ends with an appendix about the homogenization of knot concordance homomorphisms.
-
On classical upper bounds for slice genera. [ArXiv:1611.02679] [Selecta Math.]
With Lukas Lewark.Abstract: We introduce a new link invariant called the algebraic genus, which gives an upper bound for the topological slice genus of links. In fact, the algebraic genus is an upper bound for another version of the slice genus proposed here: the minimal genus of a surface in the four-ball whose complement has infinite cyclic fundamental group. We characterize the algebraic genus in terms of cobordisms in three-space, and explore the connections to other knot invariants related to the Seifert form, the Blanchfield form, knot genera and unknotting. Employing Casson-Gordon invariants, we discuss the algebraic genus as a candidate for the optimal upper bound for the topological slice genus that is determined by the S-equivalence class of Seifert matrices.
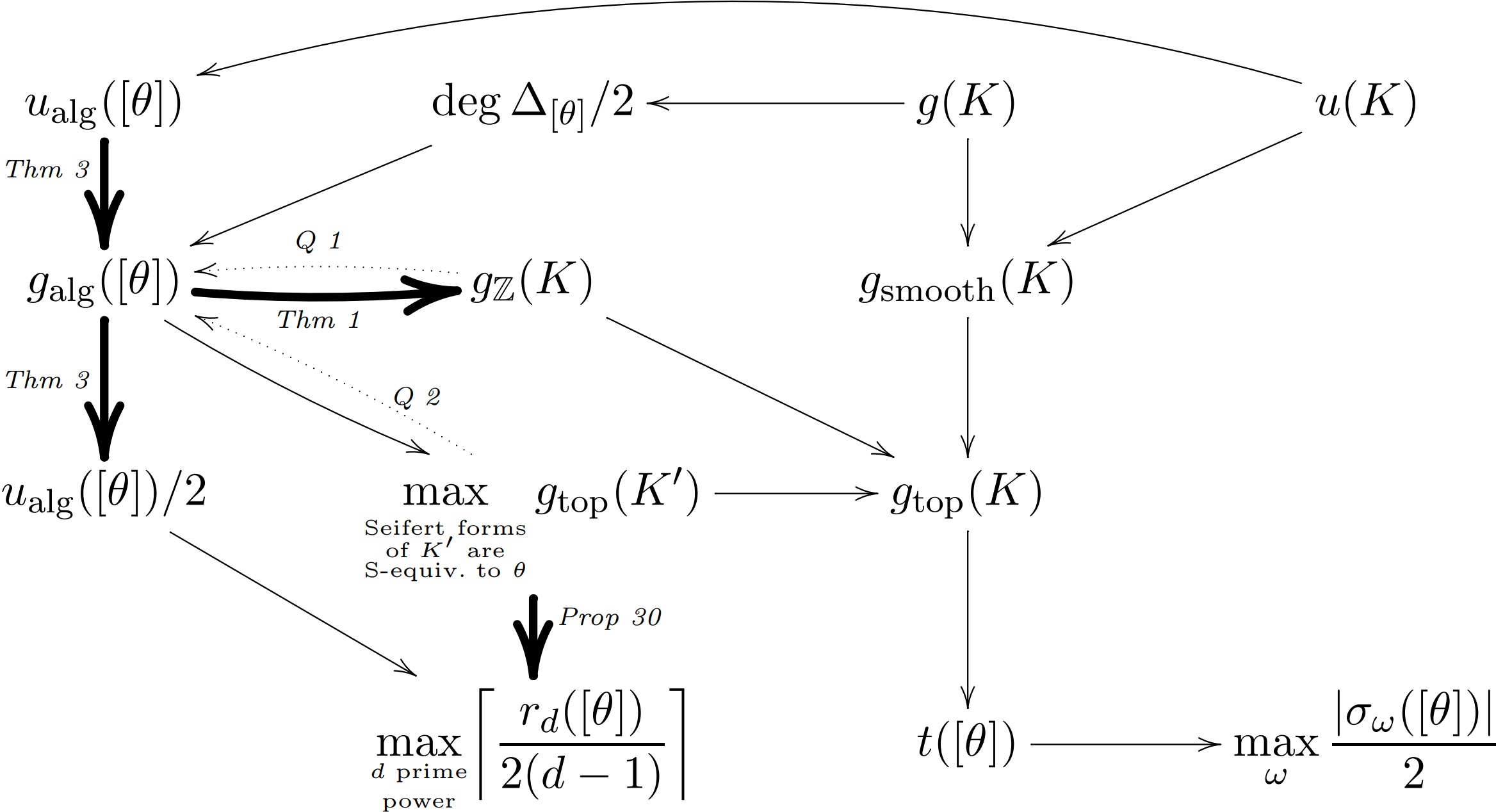 Classical invariants ... :
To a knot one can associate a Seifert matrix, which is well-defined on isotopy classes of knots up to so-called S-equivalence.
Knot invariants determined by the S-equivalence classes of Seifert matrices associated
with a knot are arguably among the simplest knot invariants. Such knot invariants are said to be `classical'.
The best-known example is the Alexander polynomial of a knot.
Classical invariants ... :
To a knot one can associate a Seifert matrix, which is well-defined on isotopy classes of knots up to so-called S-equivalence.
Knot invariants determined by the S-equivalence classes of Seifert matrices associated
with a knot are arguably among the simplest knot invariants. Such knot invariants are said to be `classical'.
The best-known example is the Alexander polynomial of a knot.
... are geometric, ... : More geometrically, two knots have the same classical invariants if and only if the first homology group of the infinite cyclic cover of their complements are isomorphic (as ℤ[t,1/t]-modules together with a natural pairing called the Blanchfield pairing). In other words, this first homology group (with pairing structure) is the `universal' classical invariant. The Alexander polynomial is the order (as ℤ[t,1/t]-modul) of this homology group and a knot has Alexander polynomial 1 if and only if this homology group is trivial.
... correspond to the first interesting term in the derived series ... : Let G denote the fundamental group of the complement of a knot. The isomorphism type of G is essentially (peripheral structure!) a complete knot invariant. By Alexander duality G/[G,G] is infinite cyclic, making [G,G]/[[G,G],[G,G]] (aka the first homology group of the infinite cyclic cover of the knot complement) the first interesting entry in the derived series of G. Of course [G,G]/[[G,G],[G,G]] (with its Blanchfield pairing up to appropriate isomorphy) is the universal classical invariant described above.
... and give upper bounds for the topological 4-genus: Surprisingly, for a knot to have the same classical invariants as the unknot (which is equivalent to having Alexander polynomial 1) is equivalent to the following concordance theory statement: the knot arises as the boundary of a locally flat disc in the 4-ball such that the fundamental group of its complement is cyclic.* This is a celebrated consequence of Freedman's Disk Embedding Theorem. This article defines the so-called algebraic genus (purely in terms of S-equivalences of Seifert matrices), which bundles earlier classical invariant considerations into a classical invariant that provides a (conjecturally optimal with in classical invariants) upper bound on the topological 4-ball genus of knots. The above result by Freedman is a crucial input and can be understood as the `genus-zero case' of our work. The diagram illustrates connections of the algebraic genus galg to other knot invariants. Arrows indicate inequality, dotted arrows are conjectural, and [θ] indicates that an invariant is classical (aka only depends on the S-equivalance class [θ] of Seifert matrices).
* While correct in the first preprint, the unfortunate typo of dropping the fundamental group condition in that statement found its way into the published version; see equation (1). We apologize. -
Khovanov width and dealternation number of positive braid links. [ArXiv:1610.04534] [Math. Res. Lett.]
With Sebastian Baader, Lukas Lewark, and Raphael Zentner.Abstract: We give asymptotically sharp upper bounds for the Khovanov width and the dealternation number of positive braid links, in terms of their crossing number. The same braid-theoretic technique, combined with Ozsv\'ath, Stipsicz, and Szab\'o's Upsilon invariant, allows us to determine the exact cobordism distance between torus knots with braid index two and six.
-
Uniqueness of Embeddings of the Affine Line into Algebraic Groups. [ArXiv:1609.02113] [J. Algebraic Geom.]
With Immanuel van Santen.Abstract: Let Y be the underlying variety of a connected affine algebraic group. We prove that two embeddings of the affine line C into Y are the same up to an automorphism of Y provided that Y is not isomorphic to a product of a torus (C*)^k and one of the three varieties C^3, SL_2, and PSL_2.
Poster: One page overview PDF of the main result, context, and idea of proof, arranged by Immanuel van Santen for a poster session.
-
On the Upsilon invariant and satellite knots. [ArXiv:1604.04901] [Math. Z.]
With JungHwan Park and Arunima Ray.Abstract: We study the effect of satellite operations on the Upsilon invariant of Ozsvath-Stipsicz-Szabo. We obtain results concerning when a knot and its satellites are independent; for example, we show that the set (D_{2^i,1})_i=1^{infinity} is a basis for an infinite rank summand of the group of smooth concordance classes of topologically slice knots, for D the positive clasped untwisted Whitehead double of any knot with positive tau-invariant, e.g. the right-handed trefoil. We also prove that the image of the Mazur satellite operator on the smooth knot concordance group contains an infinite rank subgroup of topologically slice knots.
-
On cobordisms between knots, braid index, and the Upsilon-invariant. [ArXiv:1602.02637] [Math. Ann.]
With David Krcatovich.Abstract: We use Ozsv\'ath, Stipsicz, and Szab\'o's Upsilon-invariant to provide bounds on cobordisms between knots that `contain full-twists'. In particular, we recover and generalize a classical consequence of the Morton-Franks-Williams inequality for knots: positive braids that contain a positive full-twist realize the braid index of their closure. We also establish that quasi-positive braids that are sufficiently twisted realize the minimal braid index among all knots that are concordant to their closure. Finally, we provide inductive formulas for the Upsilon invariant of torus knots and compare it to the Levine-Tristram signature profile.
-
On the topological 4-genus of torus knots. [ArXiv:1509.07634] [Trans. Amer. Math. Soc.]
With Sebastian Baader, Lukas Lewark, and Livio Liechti.Abstract: We prove that the topological locally flat slice genus of large torus knots takes up less than three quarters of the ordinary genus. As an application, we derive the best possible linear estimate of the topological slice genus for torus knots with non-maximal signature invariant.
-
Alternating numbers of torus knots with small braid index. [ArXiv:1508.05825] [Indiana Univ. Math. J.]
With Simon Pohlmann and Raphael Zentner.Abstract: We calculate the alternating number of torus knots with braid index 4 and less. For the lower bound, we use the upsilon-invariant recently introduced by Ozsv\'ath, Stipsicz, and Szab\'o. For the upper bound, we use a known bound for braid index 3 and a new bound for braid index 4. Both bounds coincide, so that we obtain a sharp result.
-
On 2-bridge knots with differing smooth and topological slice genera. [ArXiv:1508.01431] [Proc. Amer. Math. Soc.]
With Duncan McCoy.Abstract: We give infinitely many examples of 2-bridge knots for which the topological and smooth slice genera differ. The smallest of these is the 12-crossing knot 12a255. These also provide the first known examples of alternating knots for which the smooth and topological genera differ.
-
A sharp signature bound for positive four-braids. [ArXiv:1508.00418] [Q. J. Math.]
Abstract: We provide the optimal linear bound for the signature of positive four-braids in terms of the three-genus of their closures. As a consequence, we improve previously known linear bounds for the signature in terms of the first Betti number for all positive braid links. We obtain our results by combining bounds for positive three-braids with Gordon and Litherland's approach to signature via unoriented surfaces and their Goeritz forms. Examples of families of positive four-braids for which the bounds are sharp are provided.
-
The degree of the Alexander polynomial is an upper bound for the topological slice genus. [ArXiv:1504.01064] [Geom. Topol.]
Abstract: We use the famous knot-theoretic consequence of Freedman's disc theorem—knots with trivial Alexander polynomial bound a locally-flat disc in the 4-ball—to prove the following generalization. The degree of the Alexander polynomial of a knot is an upper bound for twice its topological slice genus. We provide examples of knots where this determines the topological slice genus.
-
Optimal Cobordisms between Torus Knots. [ArXiv:1501.00483] [Comm. Anal. Geom.]
Abstract: We construct cobordisms of small genus between torus knots and use them to determine the cobordism distance between torus knots of small braid index. In fact, the cobordisms we construct arise as the intersection of a smooth algebraic curve in C^2 with the unit 4-ball from which a 4-ball of smaller radius is removed. Connections to the realization problem of A_n-singularities on algebraic plane curves and the adjacency problem for plane curve singularities are discussed. To obstruct the existence of cobordisms, we use Ozsv\'ath, Stipsicz, and Szab\'o's Upsilon-invariant, which we provide explicitly for torus knots of braid index 3 and 4.
-
Holomorphically Equivalent Algebraic Embeddings. [ArXiv:1409.7319], permanently a preprint.*
With Immanuel van Santen.Abstract: We prove that two algebraic embeddings of a smooth variety X in C^m are the same up to a holomorphic coordinate change, provided that 2dim(X)+1 is smaller than or equal to m. This improves an algebraic result of Nori and Srinivas. For the proof we extend a technique of Kaliman using generic linear projections of C^m.
* Never submitted or planed to be submitted for peer-reviewed publication since, after a first version of this article appeared on the arXiv, the authors were informed that the main result was previously established by Shulim Kaliman in [ArXiv:1309.3791] [Proc. Amer. Math. Soc.]. -
Signature and the Alexander polynomial. (An appendix to Livio Liechti's `Signature, positive Hopf plumbing and the Coxeter transformation.' [ArXiv:1401.5336] [Osaka J. Math.])
With Livio Liechti. -
The signature of positive braids is linearly bounded by their first Betti number. [ArXiv:1311.1242] [Internat. J. Math.]
Abstract: We provide linear lower bounds for the signature of positive braids in terms of the three genus of their braid closure. This yields linear bounds for the topological slice genus of knots that arise as closures of positive braids.
-
Gordian adjacency for torus knots. [ArXiv:1301.5248] [Algebr. Geom. Topol.]
Abstract: A knot K is called Gordian adjacent to a knot L if there exists an unknotting sequence for L containing K. We provide a sufficient condition for Gordian adjacency of torus knots via the study of knots in the thickened torus. We also completely describe Gordian adjacency for torus knots of index 2 and 3 using Levine-Tristram signatures as obstructions to Gordian adjacency. Finally, Gordian adjacency for torus knots is compared to the notion of adjacency for plane curve singularities.