bem::LaplaceHyp< F > Class Template Referenceabstract

Bilinear form to compute the Laplace hypersingular operator. More...

#include <bform.hh>

Inheritance diagram for bem::LaplaceHyp< F >:

Public Member Functions
virtual LaplaceHyp *	clone () const
	Virtual constructor. More...
virtual BilinearForm *	clone () const=0
	Virtual constructor. More...
	LaplaceHyp (uint stroud=0, uint gauss=0, concepts::Real dist=0.0)
	Constructor. More...
void	operator() (const concepts::Element< F > &elmX, const concepts::Element< F > &elmY, concepts::ElementMatrix< F > &em)
	Application operator. More...
virtual void	operator() (const Element< typename Realtype< concepts::Real >::type > &elmX, const Element< typename Realtype< concepts::Real >::type > &elmY, ElementMatrix< concepts::Real > &em) const=0
	Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em. More...
virtual void	operator() (const Element< typename Realtype< concepts::Real >::type > &elmX, const Element< typename Realtype< concepts::Real >::type > &elmY, ElementMatrix< concepts::Real > &em, const ElementPair< typename Realtype< concepts::Real >::type > &ep) const
	Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em. More...
void	operator() (const Linear3d000< F > &elmX, const Linear3d000< F > &elmY, concepts::ElementMatrix< F > &em)

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream. More...

Private Attributes
concepts::Real	dist_
	Distance to distinguish between one point integration formula and integration using the given number of integration points. More...
uint	gauss_
LplGal008< F >	qrA_
	Class used for integration. More...
uint	stroud_
	Number of integration points. More...

Detailed Description

template<class F = concepts::Real>
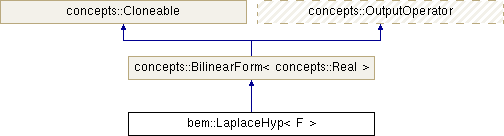
class bem::LaplaceHyp< F >

Bilinear form to compute the Laplace hypersingular operator.

Parameters

F	Field (Real or Cmplx)

Definition at line 340 of file bform.hh.

Constructor & Destructor Documentation

LaplaceHyp()

template<class F >

bem::LaplaceHyp< F >::LaplaceHyp ( uint  stroud = 0, uint  gauss = 0, concepts::Real  dist = 0.0  )

inline

Constructor.

Parameters

stroud	Number of integration points
gauss	Number of integration points
dist	Minimal distance to apply one point quadrature rule.

Definition at line 380 of file bform.hh.

Member Function Documentation

clone() [1/2]

template<class F = concepts::Real>

virtual LaplaceHyp* bem::LaplaceHyp< F >::clone ( ) const

inlinevirtual

Virtual constructor.

Returns a pointer to a copy of itself. The caller is responsible to destroy this copy.

Implements concepts::Cloneable.

Definition at line 375 of file bform.hh.

clone() [2/2]

virtual BilinearForm* concepts::BilinearForm< concepts::Real , typename Realtype<concepts::Real >::type >::clone ( ) const

pure virtualinherited

Virtual constructor.

Returns a pointer to a copy of itself. The caller is responsible to destroy this copy.

info()

virtual std::ostream& concepts::BilinearForm< concepts::Real , typename Realtype<concepts::Real >::type >::info ( std::ostream &  os ) const

protectedvirtualinherited

Returns information in an output stream.

Reimplemented from concepts::OutputOperator.

operator()() [1/4]

template<class F = concepts::Real>

void bem::LaplaceHyp< F >::operator()	(	const concepts::Element< F > &	elmX,
		const concepts::Element< F > &	elmY,
		concepts::ElementMatrix< F > &	em
	)

Application operator.

Exceptions

MissingFeature

Parameters

elmX	Element
elmY	Element
em	Element matrix for the two given elements.

operator()() [2/4]

virtual void concepts::BilinearForm< concepts::Real , typename Realtype<concepts::Real >::type >::operator() ( const Element< G > &  elmX, const Element< G > &  elmY, ElementMatrix< F > &  em  ) const

pure virtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element (test functions)
elmY	Right element (trial functions)
em	Return element matrix

operator()() [3/4]

virtual void concepts::BilinearForm< concepts::Real , typename Realtype<concepts::Real >::type >::operator() ( const Element< G > &  elmX, const Element< G > &  elmY, ElementMatrix< F > &  em, const ElementPair< G > &  ep  ) const

inlinevirtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em.

If this method is not reimplemented in a derived class, the default behaviour is to call the application operator without ep.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element
elmY	Right element
em	Return element matrix
ep	Element pair holding more information on the pair elmX and elmY

Definition at line 57 of file bilinearForm.hh.

operator()() [4/4]

template<class F >

void bem::LaplaceHyp< F >::operator() ( const Linear3d000< F > &  elmX, const Linear3d000< F > &  elmY, concepts::ElementMatrix< F > &  em  )

inline

Definition at line 386 of file bform.hh.

Member Data Documentation

dist_

template<class F = concepts::Real>

concepts::Real bem::LaplaceHyp< F >::dist_

private

Distance to distinguish between one point integration formula and integration using the given number of integration points.

Definition at line 350 of file bform.hh.

gauss_

template<class F = concepts::Real>

uint bem::LaplaceHyp< F >::gauss_

private

Definition at line 346 of file bform.hh.

qrA_

template<class F = concepts::Real>

LplGal008<F> bem::LaplaceHyp< F >::qrA_

private

Class used for integration.

Definition at line 343 of file bform.hh.

stroud_

template<class F = concepts::Real>

uint bem::LaplaceHyp< F >::stroud_

private

Number of integration points.

Definition at line 346 of file bform.hh.

---

The documentation for this class was generated from the following file:

• bem/bform.hh