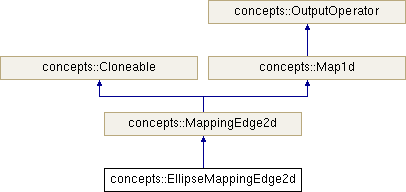
concepts::EllipseMappingEdge2d Class Reference
2D element map for an ellipsoidal arc (not skewed) More...
#include <elementMaps.hh>
Public Member Functions | |
| virtual EllipseMappingEdge2d * | clone () const |
| Virtual copy constructor. More... | |
| virtual Real | curvature (const Real t, uint n=0) const |
| Returns the n-th derivative of the curvature. More... | |
| virtual Real2d | derivative (const Real t, const uint n=1) const |
| Returns the n-th derivative. More... | |
| EllipseMappingEdge2d (const EllipseMappingEdge2d &edgemap) | |
| Copy Constructor. More... | |
| EllipseMappingEdge2d (const Real2d center, const Real a, const Real b, const Real2d vtx0, const Real2d vtx1) | |
| Constructor. More... | |
| virtual EllipseMappingEdge2d * | inverse () const |
| Returns the mapping of the edge in inverse direction. More... | |
| Real2d | n0 (const Real t) const |
| Returns the normalised right normal vector. More... | |
| virtual Real2d | normal (const Real t) const |
| Returns the right normal vector, length is that of the derivative. More... | |
| virtual Real2d | operator() (const Real t) const |
| Application operator. More... | |
| EllipseMappingEdge2d * | part (const Real t0, const Real t1) const |
| Returns a new object of an element map for a rectangular part of the reference cell defined by the two points. More... | |
| const Real2d & | vtx (uint i) const |
| Spit out one vertex of the edge. More... | |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. More... | |
Protected Attributes | |
| Real2d | vtx_ [2] |
| Coordinates of the vertices at either end of the edge. More... | |
Private Member Functions | |
| EllipseMappingEdge2d (const Real2d center, const Real a, const Real b, const Real angle0, const Real angle1) | |
Private Attributes | |
| Real | a_ |
| Half axes. More... | |
| Real | angle0_ |
| Angles between one vertex and the ellipse center. More... | |
| Real | angle1_ |
| Real | b_ |
| Real2d | m_ |
| Mid point of the ellipse. More... | |
Detailed Description
2D element map for an ellipsoidal arc (not skewed)
The edge is given by two vertices, the center and the two half axes.
This class may be used in connection with BlendingQuad2d.
- See also
- BlendingQuad2d
Definition at line 338 of file elementMaps.hh.
Constructor & Destructor Documentation
◆ EllipseMappingEdge2d() [1/3]
| concepts::EllipseMappingEdge2d::EllipseMappingEdge2d | ( | const Real2d | center, |
| const Real | a, | ||
| const Real | b, | ||
| const Real2d | vtx0, | ||
| const Real2d | vtx1 | ||
| ) |
Constructor.
- Parameters
-
center center of the ellipse a,b length of the half axes vtx0,vtx1 coordinates of the vertices
◆ EllipseMappingEdge2d() [2/3]
| concepts::EllipseMappingEdge2d::EllipseMappingEdge2d | ( | const EllipseMappingEdge2d & | edgemap | ) |
Copy Constructor.
◆ EllipseMappingEdge2d() [3/3]
|
private |
Member Function Documentation
◆ clone()
|
virtual |
Virtual copy constructor.
Implements concepts::MappingEdge2d.
◆ curvature()
Returns the n-th derivative of the curvature.
It's implemented in general for n = 0,1 and works with curved edges. Can be overwritten in derived classes for performance reasons.
Reimplemented in concepts::MappingStraightEdge2d, concepts::InverseMappingEdge2d, concepts::MappingParallelEdge2d, and concepts::CircleMappingEdge2d.
◆ derivative()
|
virtual |
Returns the n-th derivative.
Implements concepts::MappingEdge2d.
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Reimplemented from concepts::MappingEdge2d.
◆ inverse()
|
virtual |
Returns the mapping of the edge in inverse direction.
Reimplemented from concepts::MappingEdge2d.
◆ n0()
Returns the normalised right normal vector.
Definition at line 107 of file elementMaps.hh.
◆ normal()
Returns the right normal vector, length is that of the derivative.
◆ operator()()
Application operator.
Maps the point from the parameter domain onto the physical space.
Implements concepts::MappingEdge2d.
◆ part()
|
virtual |
Returns a new object of an element map for a rectangular part of the reference cell defined by the two points.
Reimplemented from concepts::MappingEdge2d.
◆ vtx()
|
inlineinherited |
Spit out one vertex of the edge.
Definition at line 124 of file elementMaps.hh.
Member Data Documentation
◆ a_
|
private |
Half axes.
Definition at line 363 of file elementMaps.hh.
◆ angle0_
|
private |
Angles between one vertex and the ellipse center.
Definition at line 365 of file elementMaps.hh.
◆ angle1_
|
private |
Definition at line 365 of file elementMaps.hh.
◆ b_
|
private |
Definition at line 363 of file elementMaps.hh.
◆ m_
|
private |
Mid point of the ellipse.
Definition at line 361 of file elementMaps.hh.
◆ vtx_
|
protectedinherited |
Coordinates of the vertices at either end of the edge.
Definition at line 128 of file elementMaps.hh.
The documentation for this class was generated from the following file:
- geometry/elementMaps.hh

