|
| void | addElements_ (const uint cKey, const typename JacobianCell< dim >::cell &cell, const HashMap< const concepts::ElementWithCell< G > * > &mapToElm, HashMap< HashMap< const concepts::ElementWithCell< G > * > > &cCtE) |
| |
| void | build_directMap_ (const typename JacobianCell< dim >::cell *cell, const concepts::HashMap< const concepts::ElementWithCell< G > * > &mapToElm) |
| | Method to build the O(1) access mapping defined via maxDoI . More...
|
| |
| void | buildBoxCandidates_ (const Point< Real, dim > P, concepts::Set< CellStripeElement< dim > > &box) const |
| | Build Boxes of Vertex Cells that contain the point P. More...
|
| |
| bool | checkCCells_ (const std::set< typename CellType< dim >::cell * > &allCell, typename std::set< typename CellType< dim >::cell * >::const_iterator iter) |
| | Method checks for the preassumed of ordered Cells, starting with coarsest cells, then finer ones etc. More...
|
| |
| bool | compute0_ (const typename JacobianCell< dim >::cell &cCell, const Point< Real, dim > &P, const Point< Real, dim > &cEta, const Real t, F &val) const |
| | Evaluates the ElementFormula in the case of coarse Cell with key cKey has a local mapping. More...
|
| |
| bool | compute1_ (const typename JacobianCell< dim >::cell &cCell, const Point< Real, dim > &P, const Point< Real, dim > &cEta, const Real t, F &val) const |
| | Evaluates the ElementFormula in the case of coarse Cell using quasi-binary search in the dichotomic tree. More...
|
| |
| F | compute_ (const Point< Real, dim > &p, const Real t) const |
| | Internal evaluation of local coordinate in the source space and its corresponding element. More...
|
| |
| | FormulaFromElementFormula (const concepts::ElementFormulaContainer< F, G > frm, const concepts::RCP< const concepts::Set< uint > > s_attrb, const concepts::RCP< const concepts::Set< uint > > d_attrb, const Point< Real, dim > scale, const Point< Real, dim > shift, const uint N, const uint cardF_2, const Real tol, const Real interior, const concepts::Set< CellBox< dim > > cBoxes, const concepts::Set< CCell_F< dim > > rCC, const bool allowPer, const Point< Real, dim > O, const Point< Real, dim > eL, const Set< uint > mapCCells, const Set< const typename JacobianCell< dim >::cell * > coarsestCell, const Set< const typename JacobianCell< dim >::cell * > irrCCells, const concepts::HashMap< CellMap< dim, G > > mapToFinestElm, const uint maxDoI, const PNF pnf, const HashMap< HashMap< const concepts::ElementWithCell< G > * > > coarseToElm) |
| |
| void | getExtremalLevel (const typename JacobianCell< dim >::cell *cell, uint(&maxL)[dim], uint(&minL)[dim]) |
| |
| bool | getOrigPoint_ (const typename JacobianCell< dim >::cell &cell, const Point< Real, dim > P, Point< Real, dim > &eta, const uint N, const Real interior, const Point< Real, dim > &x0=Real3d(0.49, 0.51, 0.49)) const |
| | Projected Newton scheme based on the parameter interior. More...
|
| |
| F | handlePNF_ () const |
| |
| bool | isCoarse_ (const typename JacobianCell< dim >::cell &cell) |
| |
| template<uint dim1 = dim, typename std::enable_if< dim1==1u, uint >::type = 0> |
| void | setLocalMap_ (const typename JacobianCell< dim >::cell *coarseCell, const HashMap< const ElementWithCell< G > * > &mapToElm, CellMap< dim, G > &map, const std::array< uint, dim > idxL, const std::array< uint, dim > idxR) const |
| |
| template<uint dim2 = dim, typename std::enable_if< dim2==2u, uint >::type = 0> |
| void | setLocalMap_ (const typename JacobianCell< dim >::cell *coarseCell, const HashMap< const ElementWithCell< G > * > &mapToElm, CellMap< dim, G > &map, const std::array< uint, dim > idxL, const std::array< uint, dim > idxR) const |
| |
| template<uint dim3 = dim, typename std::enable_if< dim3==3u, uint >::type = 0> |
| void | setLocalMap_ (const typename JacobianCell< dim >::cell *coarseCell, const HashMap< const ElementWithCell< G > * > &mapToElm, CellMap< dim, G > &map, const std::array< uint, dim > idxL, const std::array< uint, dim > idxR) const |
| |
| void | shift_DBox_ (const Point< Real, dim > &p, Point< Real, dim > &P) const |
| | shifts the physical point to the default periodic box out of the destination mesh, then applies shift and scale transformation More...
|
| |
|
| bool | allowPer_ |
| | Flag defining whether the destination mesh is considered periodic for the formula projection. More...
|
| |
| const uint | cardF_2_ |
| | Square root of amount of interior points in a curved cell for distance evaluation. More...
|
| |
| concepts::Set< CellBox< dim > > | cBoxes_ |
| | Coarse boxes of vertex coarse cells. More...
|
| |
| Z2 | cCellType_ |
| | type of last Coarse Cell 0 = Coarse Cell with mapping => O(1) search 1 = Coarse cell has no boxing => O(log) search More...
|
| |
| Set< const typename JacobianCell< dim >::cell * > | coarsestCell_ |
| | Set of coarsest cells. More...
|
| |
| HashMap< HashMap< const concepts::ElementWithCell< G > * > > | coarseToElm_ |
| | maps from coarse cell key to all finest element children belonging to that coarse cell; this is kind of a bucket More...
|
| |
| const concepts::RCP< const concepts::Set< uint > > | d_attrb_ |
| | Destination attributes. More...
|
| |
| Point< Real, dim > | eL_ |
| | Size of the periodic box, in a case of a periodic formula projection. More...
|
| |
| const Real | interior_ |
| | Interior in 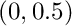 . Defines projection rule, meant to be very small. More... . Defines projection rule, meant to be very small. More...
|
| |
| Set< const typename JacobianCell< dim >::cell * > | irrCCells_ |
| | Set of coarsest cells that have an irregular children refinement pattern with irregular degree bigger as requested. More...
|
| |
| const JacobianCell< dim >::cell * | lastCell_ |
| | last cell to avoid dynamic cast More...
|
| |
| const JacobianCell< dim >::cell * | lastCoarseCell_ |
| | last coarse cell to avoid dynamic cast More...
|
| |
| const ElementWithCell< G > * | lastElm_ |
| |
| Set< uint > | mapCCells_ |
| | Keys of all coarse cells that provide local mapping. More...
|
| |
| concepts::HashMap< CellMap< dim, G > > | mapToFinestElm_ |
| |
| const uint | maxDoI_ |
| | Determines the internal map for resolving meshes with hanging nodes. More...
|
| |
| const uint | N_ |
| | Number of Newton steps. More...
|
| |
| Point< Real, dim > | O_ |
| | Origin of the periodic box, in a case of a periodic formula projection. More...
|
| |
| PNF | pnf_ |
| |
| concepts::Set< CCell_F< dim > > | rCC_ |
| | Remaining coarse cells that do not provide box design, i.e. non vertex. More...
|
| |
| const concepts::RCP< const concepts::Set< uint > > | s_attrb_ |
| | Source attributes. More...
|
| |
| const Point< Real, dim > | scale_ |
| | Scaling box, from destination mesh to source mesh. More...
|
| |
| const Point< Real, dim > | shift_ |
| | Shift box, from destination mesh to source mesh. More...
|
| |
| const Real | tol_ |
| | Stop criterion for interior Newton scheme. More...
|
| |
| const concepts::ElementFormulaContainer< F, G > | u_ |
| | The original projected formula. More...
|
| |
| bool | wasCurved_ |
| | flag is last finecell was a curved one More...
|
| |
| bool | wasCurved_c_ |
| | flag if last coarse cell was curved More...
|
| |
template<uint dim, class F, typename G = typename Realtype<F>::type>
class concepts::FormulaFromElementFormula< dim, F, G >
Projection class that allows to project an ElementFormula (i.e.
a ElementFormulaContainer) from a Space sSpc with a submesh sMsh defined by attributes onto a different Mesh that can be modified by given attributes.
It is possible that the destination Mesh dMesh is shifted or scaled. That is let the source mesh form a domain Omega_1. Let Omega_2 be a subset of Omega_1, then the destination mesh is allowed to be of the form scale * Omega_2 + shift. The scaling is allowed in each coordinate.
Furthermore the class supports periodic extensions of Elementformulas. In this case the destination mesh is bigger than the source mesh. For this we assume that the destination mesh is a periodic layer of a default box possible in various directions. The default box can be of the form scale * B + shift, where B is a subset of Omega_1. This is done with the help of the allowPeriodicity routine.
Functions build on vectorial spaces can be used as well, but the space components have to be built on the same mesh (including refinement). Then as sSpc one simply can add one particular space component and its mesh will be used. Note: If the mesh is not the same and one inserts one particular (scalar) source (space)mesh, then Newton subroutine will fail to find the cells.
This class works for tensored cells(Edge1d, Quad2d, Hexaedron3d) only in dimension 1, 2 and 3 that can be convex and non-convex as well. For an extension to more cells, the stripe algorithm and newtons start values may be adapted.
This class is not meant to provide a fast solution in terms of integration speed etc. This is clear as this class needs to compute for each point requested out of the destination space the corresponding element in the original space followed by evaluating the elementformula itsself.
Important notes:
Assume the source space msh and the destination space msh (up to scaling shiftiny and attribute modifiying) are the same, then the class does not simplify to the identity on general ElementFormulas.
However if the Elementformula is continuous over the mesh cell interfaces (points, edges, faces) then the latter holds true.
If the Elementformula is discontinuous across an interface, make sure that physical Points to evaluate do not intersect such interfaces. Then the (discrete) identity mapping remains.
Example of non identity: 1) The ElementFormla is an ElementFormulaVector<dim>(sSpc, Vector<F> sol, Grad<F>()), then it is discontinuous across interfaces. If one applies static overall trapeze integration rule, the physical Points can touch the interfaces. The interfaces has at least two adjoining elements K and L. Since the ElementFormulaVector is evaluated per element it gives different values on K and L for the same physical (and therefore adapted corresponding local ) point. Since the internal element search routine is deterministic, it is possible that the ElementformulaVector is evaluated on the Element K only for the same physical point coming from two different cells. The difference Projection - Elementformula cannot be zero in this case.
2) The projection for obvious reasons depends on the source and destination space and more important on the underlying quadrature points. Think of periodic projection of an elementformla defined on 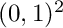 to
to 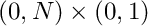 ,
, 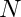 is natural. Both meshes consist of one cell only. Due to the underlying quadrature rule, the point in the destination space get stretched. The evaluation happens on different points in
is natural. Both meshes consist of one cell only. Due to the underlying quadrature rule, the point in the destination space get stretched. The evaluation happens on different points in 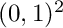 now, since physical strechted quadrature points after shifted to the default box do not coincide with original quadrature points. In this case the pointwise identity cannot hold true in general. In order to still get
now, since physical strechted quadrature points after shifted to the default box do not coincide with original quadrature points. In this case the pointwise identity cannot hold true in general. In order to still get 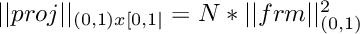 , what may is called generalized identity, one needs finer mesh and finer quadrature.
, what may is called generalized identity, one needs finer mesh and finer quadrature.
It is also possible only to project just parts of the Elementformula. This is described in the rule of attributes.
The rule of attributes:
The parameter s_attrib, shrinks the Set of all cells within the sourceSpace to look up. This applicates for example if we only want to project a part of a original solution, e.g. close to a corner etc. By default all cells are used.
The parameter d_attrib, shrinks the Set of all cells on which the projection is evaluated. If the destination cell is not requested we extend the projection by zero on these cells. By default all cells are used.
Note that (without applying scaling and shifting) the cells avaiable after shrinking by d_attrib form a domain that must be a subset of the domain formed by cells after shrinking with s_attrib. If this is not the case the underlying newton scheme cannot find a original element, and therefore an error occurs. On remaining cells not requested by d_attrib the formula is extended by zero.
Short description of underlying algorithm:
For a given physical point in the destination mesh we look for the original local coordinate and the corresponding element in the original space. We search within vertex cells by an stripe intersection that we call box search, that is a p=\infty norm idea. For non vertex cells search for the correct cell in the order of minimal distance of P and requested Set of Point evaluations of the underlying map, controlled by cardF_2. For all cells we apply newtons routine that if succeeding returns original local coordinate. Vertexcells are found in O(log(N)) where N is the number of vertex cells in the source space. Non VertexCells are found in O(N), where N is the number of non vertex Cells in the source space.
Note that the newton routine which is applied withing [0,1]^dim can have different behaviour, that is
- convergence to the loca coordinate
- leave [0,1]^dim, then we project back to the boundary
- visits vertex points (e.g by projection), then we apply interior rule
- no convergence at all, either increase Newton steps
N, the element does not contain the point, or newton scheme oscilation between same points
Note that oscilation is not handled at the moment.
Projection rule defined by interior:
Attention:
When the newton scheme ends in a Vertex of [0,1]^2, we project it to the interior of [0,1]^2, in the case of the vertex is not a solution already. Therefore the parameter interior is only allowed to be within (0,0.5).
For example the point (1, 0)^T will be projected to (1-interior, interior)^T
This applicates since in the case of vertex, the jacobian is not invertible anymore. The deriviation dependent newton scheme fails.
One workaround of the latter one could be to use derivation free root finder in the vertex endup case. Since this is supposed to be very slow, at the moment the above heuristic approach is made.
In actual practical testing this behaves nice for vertex cells, non and convex non vertex cells in 2d.
Furthermore interior should not be choosen too small, i.e. so that 1-interior = 1 in machine precision. But interior should be chosen smaller than the smallest non zero quadrature points' coordinate.
With this idea we heuristically ensure that the newton step goes away from vertex in the next step. This corresponds with an educated guess of a new startpoint.
- Precondition
- The input SpaceOnCoarseCell provides all cells strictly beginning with the coarse cells then finer cells, else a exception is thrown.
- Author
- Robert Gruhlke, 2015, 2016
-
Adrien Semin, 2016
Definition at line 518 of file formulafrmEformula.hh.

![]() to
to ![]() ,
, ![]() is natural. Both meshes consist of one cell only. Due to the underlying quadrature rule, the point in the destination space get stretched. The evaluation happens on different points in
is natural. Both meshes consist of one cell only. Due to the underlying quadrature rule, the point in the destination space get stretched. The evaluation happens on different points in ![]() now, since physical strechted quadrature points after shifted to the default box do not coincide with original quadrature points. In this case the pointwise identity cannot hold true in general. In order to still get
now, since physical strechted quadrature points after shifted to the default box do not coincide with original quadrature points. In this case the pointwise identity cannot hold true in general. In order to still get ![]() , what may is called generalized identity, one needs finer mesh and finer quadrature.
, what may is called generalized identity, one needs finer mesh and finer quadrature.![]() and with rectangle size
and with rectangle size ![]() will produce the domain
will produce the domain ![]() .
.![]() . Defines projection rule, meant to be very small.
. Defines projection rule, meant to be very small. 
