concepts::Karniadakis< type, mode > Class Template Reference
Part of the multidimensional expansion bases for the shape functions of Karniadakis and Sherwin. More...
#include <karniadakis.hh>
Public Member Functions | |
| Karniadakis (const int P, const Real *xP, const int NxP, const int Q=0, const int R=0, const bool cache=true) | |
| Constructor. More... | |
| Karniadakis (const int P, int NxP, const Real *values, const int Q=0, const int R=0) | |
| Value copy constructor. More... | |
| Karniadakis (const Karniadakis< type, mode > &arg) | |
| Copy constructor. More... | |
| uint | n () const |
| Returns the number of shape functions. More... | |
| uint | nP () const |
| Returns the number of abscissas (in which the shape functions are evaluated) More... | |
| const Real * | values () const |
| Returns the values of the shape functions. More... | |
| ~Karniadakis () | |
Static Public Member Functions | |
| static void | clearCache () |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. More... | |
Protected Attributes | |
| Real * | values_ |
| Values of the shape functions. More... | |
Private Attributes | |
| bool | cache_ |
| Cache the results of the computations in principal_H if set to true. More... | |
| uint | n_ |
| Number of shape functions. More... | |
| uint | nP_ |
| Number of points in which the shape functions are evaluated. More... | |
| Orders< type > | orders_ |
| Combines polynomial degrees and number of quadrature points. More... | |
Static Private Attributes | |
| static std::unordered_map< Orders< type >, Real *, std::hash< Orders< type > >, std::OrdersEqual< type > > | principal_H |
| Hash of the already computed values of the principal function of this type. More... | |
Detailed Description
template<int type, int mode>
class concepts::Karniadakis< type, mode >
Part of the multidimensional expansion bases for the shape functions of Karniadakis and Sherwin.
Computes one of principal functions ![]() ,
, ![]() or
or ![]() for given polynomial degrees and a set of points.
for given polynomial degrees and a set of points.
The constructor computes the values if necessary: they are stored in static hashes and can be reused if requested a second time. There is a method to get a pointer into the array of the computed values, use this at initialization time of the element to get a pointer to the values. The index of the points in which the shape functions are evaluated runs fastest, k is second and i is slowest.
- Parameters
-
type Template parameter: type of the principal function. Can take the values -
1 – The principal function
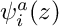 is computed in the constructor.
is computed in the constructor. -
2 – The principal function
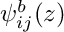 is computed in the constructor.
is computed in the constructor. -
3 – The principal function
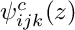 is computed in the constructor.
is computed in the constructor.
mode Template parameter: normal, derivatives, divided form. Can take the values - 0 – normal
-
1 – derivatives. The derivatives of principal function are computed in the constructor, ie.
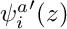 ,
, 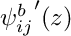 and
and 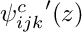 respectively, depending on the type of the principal function
respectively, depending on the type of the principal function -
2 – divided form. The principal function is divided by
 :
: 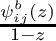 is computed in the constructor. This is only possible for the principal function
is computed in the constructor. This is only possible for the principal function 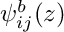 .
.
-
1 – The principal function
Definition at line 163 of file karniadakis.hh.
Constructor & Destructor Documentation
◆ Karniadakis() [1/3]
| concepts::Karniadakis< type, mode >::Karniadakis | ( | const int | P, |
| const Real * | xP, | ||
| const int | NxP, | ||
| const int | Q = 0, |
||
| const int | R = 0, |
||
| const bool | cache = true |
||
| ) |
Constructor.
Computes the values of the principal function of the given order and in the given points.
(P+1)*(Q+1)*(R+1) is the number of shape functions which have to be computed in NxP points.
- Parameters
-
P Order of the principal function in 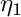
xP Points NxP Number of points Q Order of the principal function in 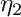
R Order of the principal function in 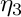
cache Controls if the computed values should be taken from and stored in the cache
◆ Karniadakis() [2/3]
| concepts::Karniadakis< type, mode >::Karniadakis | ( | const int | P, |
| int | NxP, | ||
| const Real * | values, | ||
| const int | Q = 0, |
||
| const int | R = 0 |
||
| ) |
Value copy constructor.
Copies precomputed values for the karniadakis polynomials to its value data. The chache is setted false since, the values data will be allocated.
- Parameters
-
P Order of the principal function in 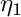
NxP Number of quadratur points values precomputed values Q Order of the principal function in 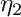
R Order of the principal function in 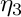
cache Controls if the computed values should be taken from and stored in the cache
◆ Karniadakis() [3/3]
| concepts::Karniadakis< type, mode >::Karniadakis | ( | const Karniadakis< type, mode > & | arg | ) |
Copy constructor.
◆ ~Karniadakis()
| concepts::Karniadakis< type, mode >::~Karniadakis | ( | ) |
Member Function Documentation
◆ clearCache()
|
inlinestatic |
Definition at line 204 of file karniadakis.hh.
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Implements concepts::ShapeFunction1D< Real >.
◆ n()
|
inlineinherited |
Returns the number of shape functions.
Definition at line 35 of file shapefunction.hh.
◆ nP()
|
inlineinherited |
Returns the number of abscissas (in which the shape functions are evaluated)
Definition at line 38 of file shapefunction.hh.
◆ values()
|
inlineinherited |
Returns the values of the shape functions.
Definition at line 40 of file shapefunction.hh.
Member Data Documentation
◆ cache_
|
private |
Cache the results of the computations in principal_H if set to true.
Definition at line 222 of file karniadakis.hh.
◆ n_
|
privateinherited |
Number of shape functions.
Definition at line 48 of file shapefunction.hh.
◆ nP_
|
privateinherited |
Number of points in which the shape functions are evaluated.
Definition at line 51 of file shapefunction.hh.
◆ orders_
|
private |
Combines polynomial degrees and number of quadrature points.
Definition at line 211 of file karniadakis.hh.
◆ principal_H
|
staticprivate |
Hash of the already computed values of the principal function of this type.
The hash is static, ie. the data is available to all instances of this class.
Definition at line 219 of file karniadakis.hh.
◆ values_
|
protectedinherited |
Values of the shape functions.
Definition at line 45 of file shapefunction.hh.
The documentation for this class was generated from the following file:
- integration/karniadakis.hh

