Public Member Functions | Static Public Member Functions | Protected Member Functions | Protected Attributes | Private Member Functions | Private Attributes | Static Private Attributes | List of all members

concepts::Quadrature< type > Class Template Reference

Basic class for numerical integration. More...

#include <quadrature.hh>

Inheritance diagram for concepts::Quadrature< type >:
concepts::OutputOperator

Public Member Functions

const Real * abscissas () const
 Returns a pointer into the array of the abscissas. More...
 
uint n () const
 Returns the number of quadrature points. More...
 
 Quadrature (uint n)
 Constructor. More...
 
const Real * weights () const
 Returns a pointer into the array of the weights. More...
 

Static Public Member Functions

static std::string storedPoints ()
 Lists the integration orders (points) which have been computed so far. More...
 

Protected Member Functions

virtual std::ostream & info (std::ostream &os) const
 Returns information in an output stream. More...
 

Protected Attributes

Real * abscissas_
 Abscissas. More...
 
Real * weights_
 Weights. More...
 

Private Member Functions

bool find_ ()
 

Private Attributes

uint n_
 Number of quadrature points. More...
 

Static Private Attributes

static std::map< uint, Real * > abscissas_H
 Hash of the already computed values of the abscissas of this rule. More...
 
static std::map< uint, Real * > weights_H
 Hash of the already computed values of the weights of this rule. More...
 

Detailed Description

template<int type>
class concepts::Quadrature< type >

Basic class for numerical integration.

This class provides the datastructures for the weights and abscissas and the methods to get them.

The values are computed in the template instantiations.

Parameters
typeTemplate parameter: type of the quadrature rule. Can take the values
  • 0: Gauss Lobatto quadrature. This rule includes both endpoints.

    \[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

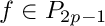    is exact for $f \in P_{2p-1}$ and n = p+1 points. n must be greater or equal to 2.
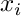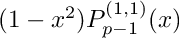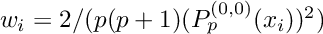    The abscissas $x_i$ are the zeros of $(1-x^2) P_{p-1}^{(1,1)}(x)$ and the weights are $w_i = 2/(p(p+1) (P_p^{(0,0)}(x_i))^2)$.
  • 1: Gauss Jacobi Lobatto quadrature. This rule includes both endpoints.

    \[ \int_{-1}^1 f(x) (1-x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

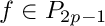    is exact for $f \in P_{2p-1}$ and n = p+1 points. n must be greater or equal to 2.
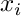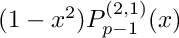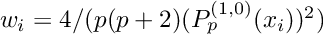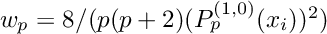    The abscissas $x_i$ are the zeros of $(1-x^2) P_{p-1}^{(2,1)}(x)$ and the weights are $w_i = 4/(p(p+2) (P_p^{(1,0)}(x_i))^2)$ and $w_p = 8/(p(p+2) (P_p^{(1,0)}(x_i))^2)$.
  • 2: Gauss Jacobi Lobatto quadrature. This rule includes both endpoints.

    \[ \int_{-1}^1 f(x) (1-x)^2 \, dx \approx \sum_{i=0}^p w_i f(x_i)\]

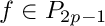    is exact for $f \in P_{2p-1}$ and n = p+1 points. n must be greater or equal to 2.
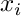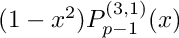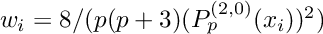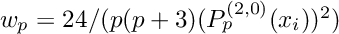    The abscissas $x_i$ are the zeros of $(1-x^2) P_{p-1}^{(3,1)}(x)$ and the weights are $w_i = 8/(p(p+3) (P_p^{(2,0)}(x_i))^2)$ and $w_p = 24/(p(p+3) (P_p^{(2,0)}(x_i))^2)$.
  • 3: Gauss Radau Jacobi quadrature. This rule includes only one of the endpoints, ie. -1.

    \[ \int_{-1}^1 f(x) (1-x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

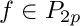    is exact for $f \in P_{2p}$ and n = p+1 points. n must be greater or equal to 2.
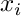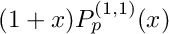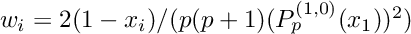    The abscissas $x_i$ are the zeros of $(1+x) P_p^{(1,1)}(x)$ and the weights are $w_i = 2(1-x_i)/(p(p+1) (P_p^{(1,0)}(x_1))^2)$.
  • 4: Gauss Jacobi quadrature. This rule does not include the endpoints -1 and 1.

    \[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]

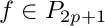    is exact for $f \in P_{2p+1}$ and n = p+1 points. n must be greater or equal to 1.
    The abscissas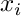 $x_i$ are the zeros of 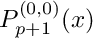$P_{p+1}^{(0,0)}(x)$ and the weights are

    \[w_i = \frac{2}{1-x_i^2} \left( \frac{d}{dx} \left. P^{(0,0)}_{p+1}(x) \right|_{x=x_i} \right)^{-2}.\]

  • 5: Trapeze quadrature. This rule include the endpoints -1 and 1.

    \[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^{n-1} w_i f(x_i) \]

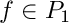    is only exact for $f \in P_{1}$. n must be greater or equal to 2.
    The abscissas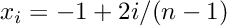 $x_i = -1 + 2i/(n-1)$ are equidistant and the weights are

    \[w_i = \frac{1}{n-1}\left\{\begin{array}{ll}1 & i \in \{0,n\}\\2 & \mbox{otherwise}\end{array}\right.\]

Requesting the same quadrature rule with the same amount of integration points several times does not harm: the values are only stored once (internally).

Test:

test::QuadratureTest

test::KarniadakisTest

Author
Philipp Frauenfelder, 2000

Definition at line 97 of file quadrature.hh.

Constructor & Destructor Documentation

◆ Quadrature()

template<int type>
concepts::Quadrature< type >::Quadrature ( uint  n)

Constructor.

Computes the quadrature points.

Parameters
nNumber of entries to be computed

Member Function Documentation

◆ abscissas()

template<int type>
const Real* concepts::Quadrature< type >::abscissas ( ) const
inline

Returns a pointer into the array of the abscissas.

Definition at line 105 of file quadrature.hh.

◆ find_()

template<int type>
bool concepts::Quadrature< type >::find_ ( )
private

◆ info()

template<int type>
virtual std::ostream& concepts::Quadrature< type >::info ( std::ostream &  os) const
protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::OutputOperator.

◆ n()

template<int type>
uint concepts::Quadrature< type >::n ( ) const
inline

Returns the number of quadrature points.

Definition at line 109 of file quadrature.hh.

◆ storedPoints()

template<int type>
static std::string concepts::Quadrature< type >::storedPoints ( )
static

Lists the integration orders (points) which have been computed so far.

Returns
a string containing the computed orders.

◆ weights()

template<int type>
const Real* concepts::Quadrature< type >::weights ( ) const
inline

Returns a pointer into the array of the weights.

Definition at line 107 of file quadrature.hh.

Member Data Documentation

◆ abscissas_

template<int type>
Real* concepts::Quadrature< type >::abscissas_
protected

Abscissas.

Definition at line 119 of file quadrature.hh.

◆ abscissas_H

template<int type>
std::map<uint, Real*> concepts::Quadrature< type >::abscissas_H
staticprivate

Hash of the already computed values of the abscissas of this rule.

The hash is static, ie. the data is available to all instances of this class.

Definition at line 127 of file quadrature.hh.

◆ n_

template<int type>
uint concepts::Quadrature< type >::n_
private

Number of quadrature points.

Definition at line 136 of file quadrature.hh.

◆ weights_

template<int type>
Real* concepts::Quadrature< type >::weights_
protected

Weights.

Definition at line 121 of file quadrature.hh.

◆ weights_H

template<int type>
std::map<uint, Real*> concepts::Quadrature< type >::weights_H
staticprivate

Hash of the already computed values of the weights of this rule.

The hash is static, ie. the data is available to all instances of this class.

Definition at line 133 of file quadrature.hh.

The documentation for this class was generated from the following file:
Page URL: http://wiki.math.ethz.ch/bin/view/Concepts/WebHome
21 August 2020
© 2020 Eidgenössische Technische Hochschule Zürich