hp3D::RefineOrRaise< F, G > Class Template Reference
Refines element or raises its polynomial degree. More...
#include <hpExtension.hh>
Public Member Functions | |
| virtual void | operator() (const concepts::Cell &cell) throw (concepts::MissingFeature) |
| Application operator. More... | |
| virtual void | operator() (const concepts::Element< F > &elm) throw (concepts::MissingFeature) |
| Application operator. More... | |
| RefineOrRaise (const concepts::Vector< F > &solution, const Real theta, concepts::AdaptiveSpace< G, concepts::AdaptiveAdjustP< 3 > > &spc) | |
| Constructor. More... | |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. More... | |
Private Member Functions | |
| bool | regression_ (concepts::Array< F > &coeff, const uint p) const |
| Makes the regression test. More... | |
| Real | transCoeff_ (const uint i, const uint j) const |
| Returns the ith coefficient of the jth shape function in a Legendre expansion. More... | |
Private Attributes | |
| concepts::Array< F > | coeff_ |
| Elementwise coefficients of the shape functions. More... | |
| concepts::Array< F > | legendre_ |
| Legendre coefficients. More... | |
| concepts::Array< F > | regr_ |
| Temporary space for the log linear regression. More... | |
| const concepts::Vector< F > & | solution_ |
| Vector of the variable to plot. More... | |
| concepts::AdaptiveSpace< G, concepts::AdaptiveAdjustP< 3 > > & | spc_ |
| Space. More... | |
| const Real | theta_ |
| Decision parameter. More... | |
Detailed Description
template<typename F, typename G = typename concepts::Realtype<F>::type>
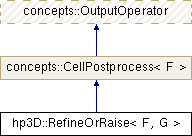
class hp3D::RefineOrRaise< F, G >
Refines element or raises its polynomial degree.
The decision is based on a log linear regression to find out if the Legendre coefficients of the solution decrease exponentially.
The parameter theta is used to control this decision. If ![]() is less than
is less than theta, the element's polynomial degree is raised, otherwise it is refined. m is the slope of the fitted line in the regression. This decision is taken anisotropic!
Definition at line 40 of file hpExtension.hh.
Constructor & Destructor Documentation
◆ RefineOrRaise()
| hp3D::RefineOrRaise< F, G >::RefineOrRaise | ( | const concepts::Vector< F > & | solution, |
| const Real | theta, | ||
| concepts::AdaptiveSpace< G, concepts::AdaptiveAdjustP< 3 > > & | spc | ||
| ) |
Constructor.
- Parameters
-
solution Solution vector theta Decision parameter spc Space (is used for the refinements)
Member Function Documentation
◆ info()
|
protectedvirtualinherited |
Returns information in an output stream.
Reimplemented from concepts::OutputOperator.
Reimplemented in concepts::CellEdgeIntegral< F >, concepts::CellFaceIntegral< F >, concepts::CellIntegral< F >, concepts::PRefinement< F, dim >, concepts::HRefinement< F, dim >, hp3D::APrioriRefinement, hp2D::APrioriRefinement, graphics::VertexList, graphics::MatrixBaseElementFormulaCell< F, G >, graphics::MatrixCounterCell, graphics::BaseMeshCell, graphics::BaseFormulaCell< F, G >, graphics::BaseElementFormulaCell< F, G >, graphics::BaseDataCell< F, G >, graphics::BaseOutputCell< F >, graphics::BaseOutputCell< typename concepts::Realtype< F >::type >, and graphics::BaseOutputCell< Real >.
◆ operator()() [1/2]
|
inlinevirtual | ||||||||||||||
Application operator.
This application operator has to be overloaded to post process a mesh.
- Parameters
-
cell Current cell
Implements concepts::CellPostprocess< F >.
Definition at line 52 of file hpExtension.hh.
◆ operator()() [2/2]
|
virtual | ||||||||||||||
Application operator.
This application operator has to be overloaded to post process a space.
- Parameters
-
elm Current element
Implements concepts::CellPostprocess< F >.
◆ regression_()
|
private |
Makes the regression test.
The coefficients in coeff are one dimensional, ie. 3D coefficients are collapsed to 1D using
![\[ |\hat a_i| = \left( \sum_{j=0}^{n_y} \sum_{k=0}^{n_z} |a_{ijk}|^2 \frac{2}{2j+1} \frac{2}{2k+1} \right)^{1/2} \]](form_577.png)
before calling this function.
- Parameters
-
coeff 1D coefficients, will be overwritten p Polynomial degree
- Returns
- true if the coefficients seem to decrease exponentially, ie. increasing p is recommended
◆ transCoeff_()
|
private |
Returns the ith coefficient of the jth shape function in a Legendre expansion.
![]()
Member Data Documentation
◆ coeff_
|
private |
Elementwise coefficients of the shape functions.
Definition at line 56 of file hpExtension.hh.
◆ legendre_
|
private |
Legendre coefficients.
Definition at line 58 of file hpExtension.hh.
◆ regr_
|
private |
Temporary space for the log linear regression.
Definition at line 60 of file hpExtension.hh.
◆ solution_
|
private |
Vector of the variable to plot.
Definition at line 62 of file hpExtension.hh.
◆ spc_
|
private |
Definition at line 64 of file hpExtension.hh.
◆ theta_
|
private |
Decision parameter.
Definition at line 66 of file hpExtension.hh.
The documentation for this class was generated from the following file:
- hp3D/hpExtension.hh

