Essential boundary conditions and multi-point constraints [1]. More...

Classes
class	AnalyticalConstraint
	Models an analytical constraint. More...

class	ConstraintsList
	List of `AnalyticalConstraint`. More...

class	Element
	Element of the constraints space. More...

class	Space
	Space of constraints. More...

Detailed Description

Essential boundary conditions and multi-point constraints [1].

The idea is to formulate the constraints as a linear system which has to be fullfilled by the solution:

$Cx = g,$

where x is the solution vector, C the constraints matrix and g its right hand side. The assumptions for g and C are as follows:

Cx = g is solveable, ie. g is in the range of C.
If a solution exists, it is unique, ie. the intersection of the kernel of C and the kernel of the stiffness matrix is trivial.
C is of full rank, ie. the conditions are linearly independent.

The last conditions asserts that $(CC^\top)^{-1}$ is well defined.

Using C and g, the constraint stiffness matrix is defined by

$S' = C^\top C + Q^\top S Q,$

where $Q = 1 - C^\top (CC^\top)^{-1} C$ (symmetric!) and the constraint right hand side is defined by

$f' = C^\top g + Q^\top(f - SRg),$

where $R = C^\top (CC^\top)^{-1}$ . Solving results in a unique solution x which satisfies the constraints Cx = g and the original problem Sx = f.

In an application, this could be used in the following way:

    constraints::ConstraintsList<Real> constrList;
Add analytical constraints to constrList

Compute C
    constraints::Space<Real> constrSpc(spc, constrList);
    concepts::SparseMatrix<Real> C(constrSpc, spc, constrList);
    concepts::SparseMatrix<Real> Ct(C, true);

Compute CCtinv
    concepts::Compose<Real> CtC(Ct, C);
    concepts::Compose<Real> CCt(C, Ct);
    concepts::SparseMatrix<Real> CCtmatrix(CCt);
    concepts::SuperLU CCtinv(CCtmatrix);

Compute R and Q
    concepts::Compose<Real> R(Ct, CCtinv);
    concepts::Compose<Real> Qmin(R, C);
    concepts::LiCoI<Real> Q(Qmin, -1.0);

Compute the stiffness matrix
    Identity mass_bf;
    concepts::SparseMatrix<Real> mass(spc, mass_bf);
    Laplace stiff_bf;
    concepts::SparseMatrix<Real> stiff(spc, stiff_bf);
    concepts::LiCo<Real> S(stiff, mass);

Compute S'
    concepts::Compose<Real> QS(Q, S);
    concepts::Compose<Real> QSQ(QS, Q);
    concepts::LiCo<Real> Sp(CtC, QSQ);

Compute g and f'
    concepts::Vector<Real> g(constrSpc, constrList);
    concepts::Vector<Real> Rg(spc);
    concepts::Vector<Real> SRg(spc);
    R(g, Rg);
    S(Rg, SRg);
    RHS rhs_lf;
    concepts::Vector<Real> f(spc, rhs_lf);
    f -= SRg;
    concepts::Vector<Real> fp(spc);
    Q(f, fp);
    Ct(g, SRg);
    fp += SRg;

    concepts::CG<Real> solver(Sp, 1e-15, 2000);
    concepts::Vector<Real> sol(spc);
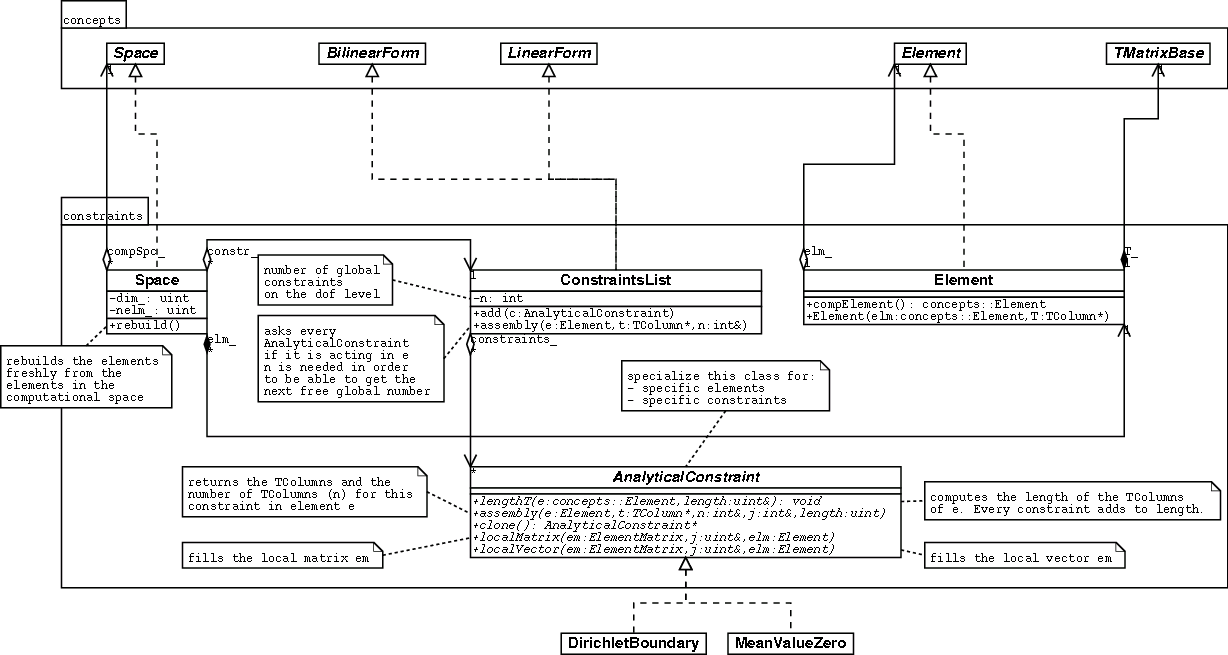
    solver(fp, sol);

The following figure gives an overview of the classes in this namespace
UML diagram of classes in namespace constraints

See also: Ainsworth, Essential boundary conditions and multi-point constraints in finite element analysis, 2000, Comput. Methods Appl Mech. Engrg. 190 (2001) 6323-6339

Author: Philipp Frauenfelder, 2002

constraints Namespace Reference

Classes

Detailed Description