Comment créer et manipuler les données scientifiques : autour de Numpy¶
Le tableau : l’outil de base du calcul scientifique
Manipulation fréquente d’ensembles ordonnés discrets :
- temps discrétisé d’une expérience/simulation
- signal enregistré par un appareil de mesure
- pixels d’une image, ...
Le module Numpy permet de
- créer d’un coup ces ensembles de données
- réaliser des opérations en “batch” sur les tableaux de données (pas de boucle sur les éléments).
Tableau de données := numpy.ndarray
La création de tableaux de données Numpy¶
Un petit exemple pour commencer:
>>> import numpy as np
>>> a = np.array([0, 1, 2])
>>> a
array([0, 1, 2])
>>> print a
[0 1 2]
>>> b = np.array([[0., 1.], [2., 3.]])
>>> b
array([[ 0., 1.],
[ 2., 3.]])
Dans la pratique, on rentre rarement les éléments un par un...
Valeurs espacées régulièrement:
>>> import numpy as np >>> a = np.arange(10) # de 0 a n-1 >>> a array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) >>> b = np.arange(1., 9., 2) # syntaxe : debut, fin, saut >>> b array([ 1., 3., 5., 7.])ou encore, en spécifiant le nombre de points:
>>> c = np.linspace(0, 1, 6) >>> c array([ 0. , 0.2, 0.4, 0.6, 0.8, 1. ]) >>> d = np.linspace(0, 1, 5, endpoint=False) >>> d array([ 0. , 0.2, 0.4, 0.6, 0.8])Constructeurs pour des tableaux classiques:
>>> a = np.ones((3,3)) >>> a array([[ 1., 1., 1.], [ 1., 1., 1.], [ 1., 1., 1.]]) >>> a.dtype dtype('float64') >>> b = np.ones(5, dtype=np.int) >>> b array([1, 1, 1, 1, 1]) >>> c = np.zeros((2,2)) >>> c array([[ 0., 0.], [ 0., 0.]]) >>> d = np.eye(3) >>> d array([[ 1., 0., 0.], [ 0., 1., 0.], [ 0., 0., 1.]])
La représentation graphique des données : matplotlib et mayavi¶
Maintenant que nous avons nos premiers tableaux de données, nous allons les visualiser. Matplotlib est un package de plot 2-D, on importe ces fonctions de la manière suivante
>>> import pylab
>>> # ou
>>> from pylab import * # pour tout importer dans le namespace
Si vous avec lancé Ipython avec python(x,y), ou avec l’option ipython -pylab (sous linux), toutes les fonctions/objets de pylab ont déjà été importées, comme si on avait fait from pylab import *. Dans la suite on suppose qu’on a fait from pylab import * ou lancé ipython -pylab: on n’écrira donc pas pylab.fonction() mais directement fonction.
Tracé de courbes 1-D
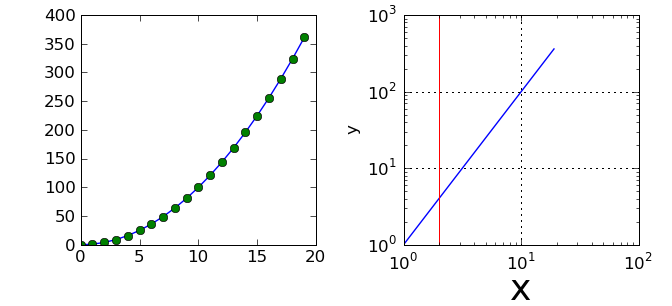
In [6]: a = np.arange(20)
In [7]: plot(a, a**2) # line plot
Out[7]: [<matplotlib.lines.Line2D object at 0x95abd0c>]
In [8]: plot(a, a**2, 'o') # symboles ronds
Out[8]: [<matplotlib.lines.Line2D object at 0x95b1c8c>]
In [9]: clf() # clear figure
In [10]: loglog(a, a**2)
Out[10]: [<matplotlib.lines.Line2D object at 0x95abf6c>]
In [11]: xlabel('x') # un peu petit
Out[11]: <matplotlib.text.Text object at 0x98923ec>
In [12]: xlabel('x', fontsize=26) # plus gros
Out[12]: <matplotlib.text.Text object at 0x98923ec>
In [13]: ylabel('y')
Out[13]: <matplotlib.text.Text object at 0x9892b8c>
In [14]: grid()
In [15]: axvline(2)
Out[15]: <matplotlib.lines.Line2D object at 0x9b633cc>
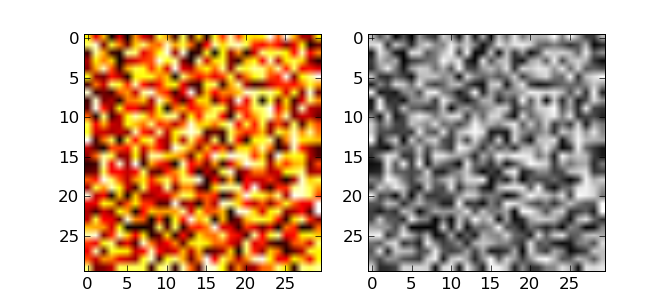
Tableaux 2-D (images par exemple)
In [48]: # Tableaux 30x30 de nombres aleatoires entre 0 et 1
In [49]: image = np.random.rand(30,30)
In [50]: imshow(image)
Out[50]: <matplotlib.image.AxesImage object at 0x9e954ac>
In [51]: gray()
In [52]: hot()
In [53]: imshow(image, cmap=cm.gray)
Out[53]: <matplotlib.image.AxesImage object at 0xa23972c>
In [54]: axis('off') # on enleve les ticks et les labels
Il y a bien d’autres fonctionnalités dans matplotlib : choix de couleurs ou des tailles de marqueurs, fontes latex, inserts à l’intérieur d’une figure, histogrammes, etc.
Pour aller plus loin :
- la documentation de matplotlib http://matplotlib.sourceforge.net/contents.html
- une gallerie d’exemples accompagnés du code source http://matplotlib.sourceforge.net/gallery.html
Représentation en 3-D
Pour la visualisation 3-D, on utilise un autre package : Mayavi. Un exemple rapide : commencez par relancer ipython avec les options ipython -pylab -wthread
In [59]: from enthought.mayavi import mlab
In [60]: mlab.figure()
get fences failed: -1
param: 6, val: 0
Out[60]: <enthought.mayavi.core.scene.Scene object at 0xcb2677c>
In [61]: mlab.surf(image)
Out[61]: <enthought.mayavi.modules.surface.Surface object at 0xd0862fc>
In [62]: mlab.axes()
Out[62]: <enthought.mayavi.modules.axes.Axes object at 0xd07892c>
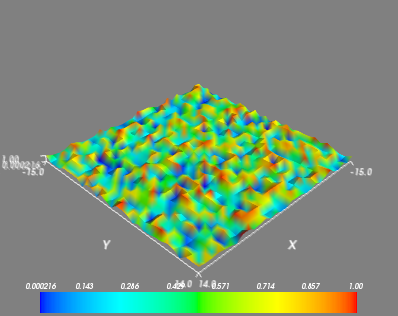
La fenêtre mayavi/mlab qui s’ouvre est interactive : en cliquant sur le bouton gauche de la souris vous pouvez faire tourner l’image, on peut zoomer avec la molette, etc.
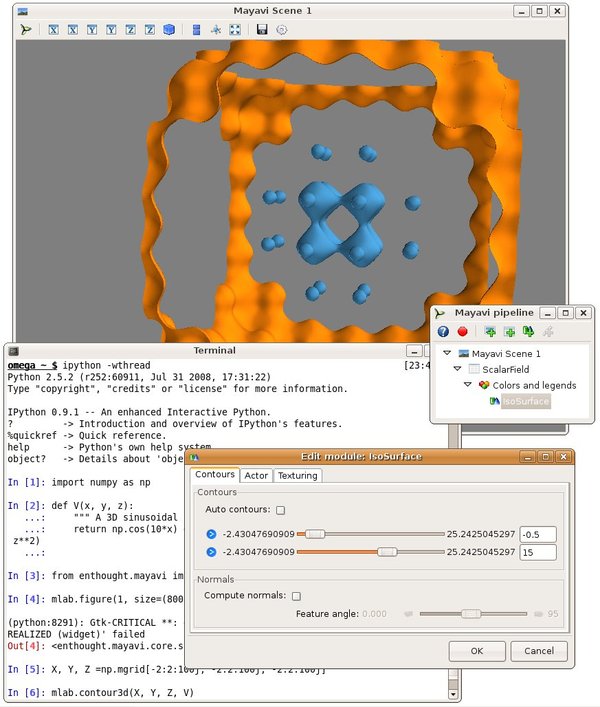
Pour plus d’informations sur Mayavi : http://code.enthought.com/projects/mayavi/docs/development/html/mayavi/index.html
Indexage¶
On peut accéder aux éléments des tableaux Numpy (indexer) d’une manière similaire que pour les autres séquences Python (list, tuple)
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[0], a[2], a[-1]
(0, 2, 9)
Attention ! L’indexage commence à partir de 0, comme pour les autres séquences Python (et comme en C/C++). En Fortran ou Matlab, l’indexage commence à 1.
Pour les tableaux multidimensionnels, l’indice d’un élément est donné par un n-uplet d’entiers
>>> a = np.diag(np.arange(5))
>>> a
array([[0, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 2, 0, 0],
[0, 0, 0, 3, 0],
[0, 0, 0, 0, 4]])
>>> a[1,1]
1
>>> a[2,1] = 10 # deuxième ligne, première colonne
>>> a
array([[ 0, 0, 0, 0, 0],
[ 0, 1, 0, 0, 0],
[ 0, 10, 2, 0, 0],
[ 0, 0, 0, 3, 0],
[ 0, 0, 0, 0, 4]])
>>> a[1]
array([0, 1, 0, 0, 0])
A retenir :
- En 2-D, la première dimension correspond aux lignes, la seconde aux colonnes.
- Pour un tableau a à plus qu’une dimension,`a[0]` est interprété en prenant tous les éléments dans les dimensions non-spécifiés.
Slicing (parcours régulier des éléments)¶
Comme l’indexage, similaire au slicing des autres séquences Python:
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[2:9:3] # [début:fin:pas]
array([2, 5, 8])
Attention, le dernier indice n’est pas inclus
>>> a[:4]
array([0, 1, 2, 3])
début:fin:pas est un objet slice, qui représente l’ensemble d’indices range(début, fin, pas). On peut créer explicitement un slice
>>> sl = slice(1, 9, 2)
>>> a = np.arange(10)
>>> b = 2*a + 1
>>> a, b
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19]))
>>> a[sl], b[sl]
(array([1, 3, 5, 7]), array([ 3, 7, 11, 15]))
On n’est pas obligé de spécifier à la fois le début (indice 0 par défaut), la fin (dernier indice par défaut) et le pas (1 par défaut):
>>> a[1:3]
array([1, 2])
>>> a[::2]
array([0, 2, 4, 6, 8])
>>> a[3:]
array([3, 4, 5, 6, 7, 8, 9])
Et bien sûr, ça marche pour les tableaux à plusieurs dimensions:
>>> a = np.eye(5)
>>> a
array([[ 1., 0., 0., 0., 0.],
[ 0., 1., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 1., 0.],
[ 0., 0., 0., 0., 1.]])
>>> a[2:4,:3] #2è et 3è lignes, trois premières colonnes
array([[ 0., 0., 1.],
[ 0., 0., 0.]])
On peut changer la valeur de tous les éléments indexés par une slice de façon très simple
>>> a[:3,:3] = 4
>>> a
array([[ 4., 4., 4., 0., 0.],
[ 4., 4., 4., 0., 0.],
[ 4., 4., 4., 0., 0.],
[ 0., 0., 0., 1., 0.],
[ 0., 0., 0., 0., 1.]])
Une petite illustration en résumé de l’indexage et du slicing avec Numpy...
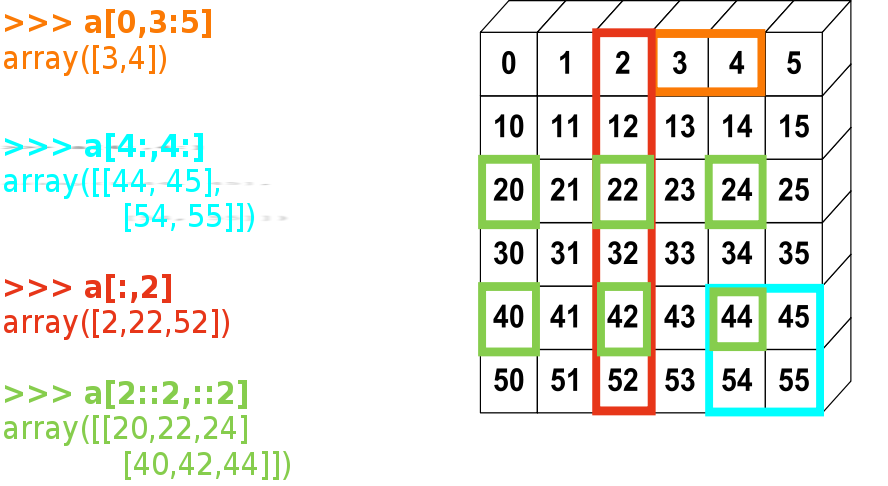
Une opération de slicing crée une vue (view) du tableau d’origine, c’est-à-dire une manière d’aller lire dans la mémoire. Le tableau d’origine n’est donc pas copié. Quand on modifie la vue, on modife aussi le tableau d’origine.:
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b = a[::2]; b
array([0, 2, 4, 6, 8])
>>> b[0] = 12
>>> b
array([12, 2, 4, 6, 8])
>>> a # a a été modifié aussi !
array([12, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Ce comportement peut surprendre au début... mais est bien pratique pour gérer la mémoire de façon économe.
Si on veut faire une copie différente du tableau d’origine
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b = np.copy(a[::2]); b
array([0, 2, 4, 6, 8])
>>> b[0] = 12
>>> b
array([12, 2, 4, 6, 8])
>>> a # a n'a pas été modifié
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Manipuler la forme des tableaux¶
On obtient la forme d’un tableau grâce à la méthode ndarray.shape qui retourne un tuple des dimensions du tableau
>>> a = np.arange(10)
>>> a.shape
(10,)
>>> b = np.ones((3,4))
>>> b.shape
(3, 4)
>>> b.shape[0] # on peut accéder aux élements du tuple b.shape
3
>>> # et on peut aussi faire
>>> np.shape(b)
(3, 4)
Par ailleurs on obtient la longueur de la première dimension avec np.alen (par analogie avec len pour une liste) et le nombre total d’éléments avec ndarray.size:
>>> np.alen(b)
3
>>> b.size
12
Il existe plusieurs fonctions Numpy qui permettent de créer un tableau de taille différente à partir d’un tableau de départ.:
>>> a = np.arange(36)
>>> b = a.reshape((6, 6))
>>> b
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]])
ndarray.reshape renvoie une vue, et pas une copie
>>> b[0,0] = 10
>>> a
array([10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35])
On peut aussi créer un tableau avec un nombre d’éléments différents avec ndarray.resize:
>>> a = np.arange(36)
>>> a.resize((4,2))
>>> a
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
>>> b = np.arange(4)
>>> b.resize(3, 2)
>>> b
array([[0, 1],
[2, 3],
[0, 0]])
Ou paver un grand tableau à partir d’un tableau plus petit
>>> a = np.arange(4).reshape((2,2))
>>> a
array([[0, 1],
[2, 3]])
>>> np.tile(a, (2,3))
array([[0, 1, 0, 1, 0, 1],
[2, 3, 2, 3, 2, 3],
[0, 1, 0, 1, 0, 1],
[2, 3, 2, 3, 2, 3]])
Exercices : quelques gammes avec les tableaux numpy¶
Grâce aux divers constructeurs, à l’indexage et au slicing, et aux opérations simples sur les tableaux (+/-/x/:), on peut facilement créer des tableaux de grande taille correspondant à des motifs variés.
Exemple : comment créer le tableau:
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 0]
[15 16 17 18 19]
[20 21 22 23 24]]
Réponse
>>> a = np.arange(25).reshape((5,5))
>>> a[2, 4] = 0
Exercices : créer les tableaux suivants de la manière la plus simple possible (pas élément par élement)
[[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]
[ 1. 1. 1. 2.]
[ 1. 6. 1. 1.]]
[[0 0 0 0 0]
[2 0 0 0 0]
[0 3 0 0 0]
[0 0 4 0 0]
[0 0 0 5 0]
[0 0 0 0 6]]
Réponses Création de tableaux
De “vraies données” : lire et écrire des tableaux dans des fichiers¶
Bien souvent, nos expériences ou nos simulations écrivent leurs résultats dans des fichiers. Il faut ensuite les charger dans Python sous la forme de tableaux Numpy pour les manipuler. De même, on peut vouloir sauver les tableaux qu’on a obtenus dans des fichiers.
Aller dans le bon répertoire
Pour se déplacer dans une arborescence de fichiers :
utiliser les fonctionnalités d’Ipython : cd, pwd, tab-completion.
modules os (routines système) et os.path (gestion des chemins)
>>> import os, os.path >>> current_dir = os.getcwd() >>> current_dir '/home/gouillar/sandbox' >>> data_dir = os.path.join(current_dir, 'data') >>> data_dir '/home/gouillar/sandbox/data' >>> if not(os.path.exists(data_dir)): ... os.mkdir('data') ... print "creation du repertoire 'data'" ... >>> os.chdir(data_dir) # ou dans Ipython : cd data
On peut en fait se servir de Ipython comme d’un véritable shell grâce aux fonctionnalités d’Ipython et au module os.
Ecrire un tableau de données dans un fichier
>>> a = np.arange(100)
>>> a = a.reshape((10, 10))
Ecriture dans un fichier texte (en ascii)
>>> np.savetxt('data_a.txt', a)
Ecriture dans un fichier en binaire (extension .npy)
>>> np.save('data_a.npy', a)
Charger un tableau de données à partir d’un fichier
Lecture dans un fichier texte
>>> b = np.loadtxt('data_a.txt')
Lecture dans un fichier binaire
>>> c = np.load('data_a.npy')
Pour lire les fichiers de données matlab
scipy.io.loadmat : la structure matlab d’un fichier .mat est stockée dans un dictionnaire.
Pour sélectionner un fichier dans une liste
On va sauver chaque ligne de a dans un fichier différent
>>> for i, l in enumerate(a):
... print i, l
... np.savetxt('ligne_'+str(i), l)
...
0 [0 1 2 3 4 5 6 7 8 9]
1 [10 11 12 13 14 15 16 17 18 19]
2 [20 21 22 23 24 25 26 27 28 29]
3 [30 31 32 33 34 35 36 37 38 39]
4 [40 41 42 43 44 45 46 47 48 49]
5 [50 51 52 53 54 55 56 57 58 59]
6 [60 61 62 63 64 65 66 67 68 69]
7 [70 71 72 73 74 75 76 77 78 79]
8 [80 81 82 83 84 85 86 87 88 89]
9 [90 91 92 93 94 95 96 97 98 99]
Pour obtenir une liste de tous les fichiers commençant par ligne, on fait appel au module glob qui “gobe” tous les chemins correspondant à un motif. Exemple
>>> import glob
>>> filelist = glob.glob('ligne*')
>>> filelist
['ligne_0', 'ligne_1', 'ligne_2', 'ligne_3', 'ligne_4', 'ligne_5', 'ligne_6', 'ligne_7', 'ligne_8', 'ligne_9']
>>> # attention la liste n'est pas toujours ordonnee
>>> filelist.sort()
>>> l2 = np.loadtxt(filelist[2])
Remarque : il est aussi possible de créer des tableaux à partir de fichiers Excel/Calc, de fichiers hdf5, etc. (mais à l’aide de modules supplémentaires non décrits ici : xlrd, pytables, etc.).
Opérations mathématiques et statistiques simples sur les tableaux¶
Un certain nombre d’opérations sur les tableaux sont codées directement dans numpy (et sont donc en général très efficaces):
>>> a = np.arange(10)
>>> a.min() # ou np.min(a)
0
>>> a.max() # ou np.max(a)
9
>>> a.sum() # ou np.sum(a)
45
Il est possible de réaliser l’opération le long d’un axe uniquement, plutôt que sur tous les éléments
>>> a = np.array([[1, 3], [9, 6]])
>>> a
array([[1, 3],
[9, 6]])
>>> a.mean(axis=0) # tableau contenant la moyenne de chaque colonne
array([ 5. , 4.5])
>>> a.mean(axis=1) # tableau contenant la moyenne de chaque ligne
array([ 2. , 7.5])
Il y en a encore bien d’autres opérations possibles : on en découvrira quelques unes au fil de ce cours.
Note
Les opérations arithmétiques sur les tableaux correspondent à des opérations élément par élément. En particulier, le produit n’est pas un produit matriciel (contrairement à Matlab) ! Le produit matriciel est fourni par np.dot:
>>> a = np.ones((2,2))
>>> a*a
array([[ 1., 1.],
[ 1., 1.]])
>>> np.dot(a,a)
array([[ 2., 2.],
[ 2., 2.]])
Exemple : simulation de diffusion avec un marcheur aléatoire

Quelle est la distance typique d’un marcheur aléatoire à l’origine, après t sauts à droite ou à gauche ?

>>> nreal = 1000 # nombre de réalisations de la marche
>>> tmax = 200 # temps sur lequel on suit le marcheur
>>> # On tire au hasard tous les pas 1 ou -1 de la marche
>>> walk = 2 * ( np.random.random_integers(0, 1, (nreal,tmax)) - 0.5 )
>>> np.unique(walk) # Vérification : tous les pas font bien 1 ou -1
array([-1., 1.])
>>> # On construit les marches en sommant ces pas au cours du temps
>>> cumwalk = np.cumsum(walk, axis=1) # axis = 1 : dimension du temps
>>> sq_distance = cumwalk**2
>>> # On moyenne dans le sens des réalisations
>>> mean_sq_distance = np.mean(sq_distance, axis=0)
In [39]: figure()
In [40]: plot(mean_sq_distance)
In [41]: figure()
In [42]: plot(np.sqrt(mean_sq_distance))
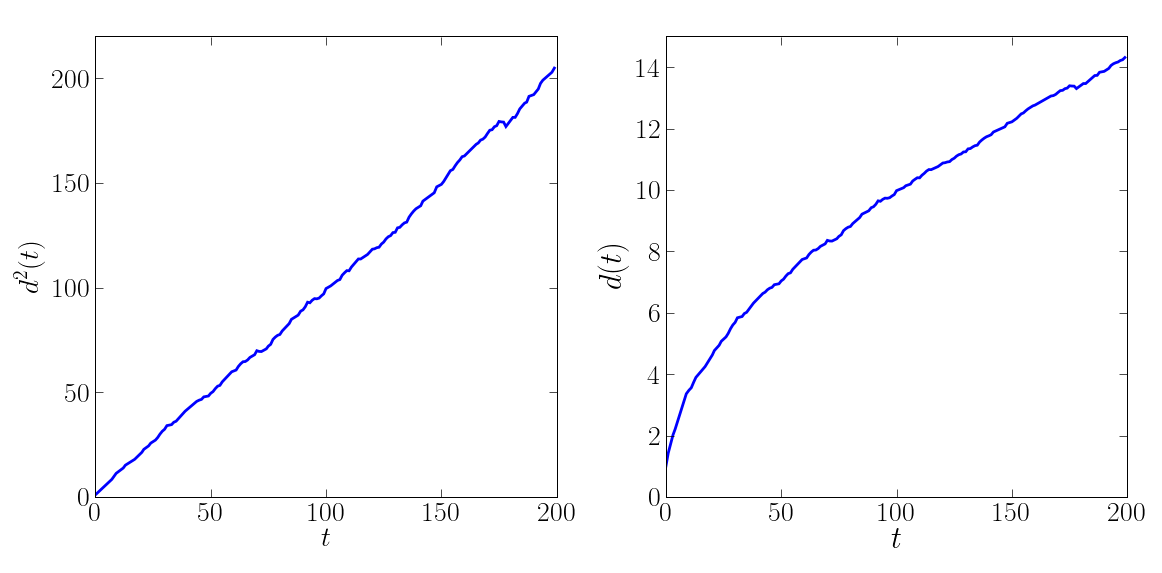
On retrouve bien que la distance grandit comme la racine carrée du temps !
Exercice : statistiques des femmes dans la recherche (données INSEE)
Récupérer les fichiers organismes.txt et pourcentage_femmes.txt (clé USB du cours ou http://www.dakarlug.org/pat/scientifique/data/).
Créer un tableau data en ouvrant le fichier pourcentage_femmes.txt avec np.loadtxt. Quelle est la taille de ce tableau ?
Les colonnes correspondent aux années 2006 à 2001. Créer un tableau annees (sans accent !) contenant les entiers correspondant à ces années.
Les différentes lignes correspondent à différents organismes de recherche dont les noms sont stockés dans le fichier organismes.txt. Créer un tableau organisms en ouvrant ce fichier. Attention : comme np.loadtxt crée par défaut des tableaux de flottant, il faut lui préciser qu’on veut créer un tableau de strings : organisms = np.loadtxt('organismes.txt', dtype=str)
Vérifier que le nombre de lignes de data est égal au nombre d’organismes.
Quel est le pourcentage maximal de femmes dans tous les organismes, toutes années confondues ?
Créer un tableau contenant la moyenne temporelle du pourcentage de femmes pour chaque organisme (i.e., faire la moyenne de data suivant l’axe No 1).
Quel organisme avait le pourcentage de femmes le plus élevé en 2004 ? (Indice np.argmax).
- Représenter un histogramme du pourcentage de femmes dans les
différents organismes en 2006 (indice : np.histogram, puis bar ou plot de matplotlib pour la visualisation).
Réponses Statistiques du pourcentage de femmes dans la recherche française
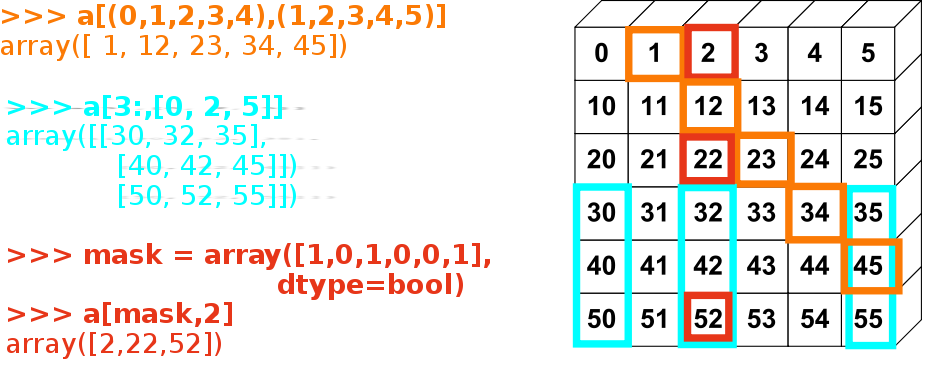
L’indexage avancé (fancy indexing)¶
On peut indexer des tableaux numpy avec des slices, mais aussi par des tableaux de booléens (les masques) ou d’entiers : on appelle ces opérations plus évoluées du fancy indexing.
Les masques
>>> np.random.seed(3)
>>> a = np.random.random_integers(0, 20, 15)
>>> a
array([10, 3, 8, 0, 19, 10, 11, 9, 10, 6, 0, 20, 12, 7, 14])
>>> (a%3 == 0)
array([False, True, False, True, False, False, False, True, False,
True, True, False, True, False, False], dtype=bool)
>>> mask = (a%3 == 0)
>>> extract_from_a = a[mask] #on pourrait écrire directement a[a%3==0]
>>> extract_from_a #on extrait un sous-tableau grâce au masque
array([ 3, 0, 9, 6, 0, 12])
Extraire un sous-tableau avec un masque produit une copie de ce sous-tableau, et non une vue
>>> extract_from_a = -1
>>> a
array([10, 3, 8, 0, 19, 10, 11, 9, 10, 6, 0, 20, 12, 7, 14])
L’indexation grâce masques peut être très utile pour l’assignation d’une nouvelle valeur à un sous-tableau
>>> a[mask] = 0
>>> a
array([10, 0, 8, 0, 19, 10, 11, 0, 10, 0, 0, 20, 0, 7, 14])
Indexer avec un tableau d’entiers
>>> a = np.arange(10)
>>> a[::2] +=3 #pour ne pas avoir toujours le même np.arange(10)...
>>> a
array([ 3, 1, 5, 3, 7, 5, 9, 7, 11, 9])
>>> a[[2, 5, 1, 8]] # ou a[np.array([2, 5, 1, 8])]
array([ 5, 5, 1, 11])
On peut indexer avec des tableaux d’entiers où le même indice est répété plusieurs fois
>>> a[[2, 3, 2, 4, 2]]
array([5, 3, 5, 7, 5])
On peut assigner de nouvelles valeurs avec ce type d’indexation
>>> a[[9, 7]] = -10
>>> a
array([ 3, 1, 5, 3, 7, 5, 9, -10, 11, -10])
>>> a[[2, 3, 2, 4, 2]] +=1
>>> a
array([ 3, 1, 6, 4, 8, 5, 9, -10, 11, -10])
Quand on crée un tableau en indexant avec un tableau d’entiers, le nouveau tableau a la même forme que le tableau d’entiers
>>> a = np.arange(10)
>>> idx = np.array([[3, 4], [9, 7]])
>>> a[idx]
array([[3, 4],
[9, 7]])
>>> b = np.arange(10)
>>> a = np.arange(12).reshape(3,4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> i = np.array( [ [0,1],
... [1,2] ] )
>>> j = np.array( [ [2,1],
... [3,3] ] )
>>> a[i,j]
array([[ 2, 5],
[ 7, 11]])
Exercice
Reprenons nos données de statistiques du pourcentage de femmes dans la recherche (tableaux data et organisms)
- Créer un tableau sup30 de même taille que data valant 1 si la valeur de data est supérieure à 30%, et 0 sinon.
- Créez un tableau contenant l’organisme avec le pourcentage de femmes le plus élévé de chaque année.
Réponses Statistiques du pourcentage de femmes dans la recherche française
Le broadcasting¶
Les opérations élémentaires sur les tableaux numpy (addition, etc.) sont faites élément par élément et opèrent donc des tableaux de même taille. Il est néanmoins possible de faire des opérations sur des tableaux de taille différente si numpy` arrive à transformer les tableaux pour qu’ils aient tous la même taille : on appelle cette transformation le broadcasting (jeu de mots intraduisible en français).
L’image ci-dessous donne un exemple de
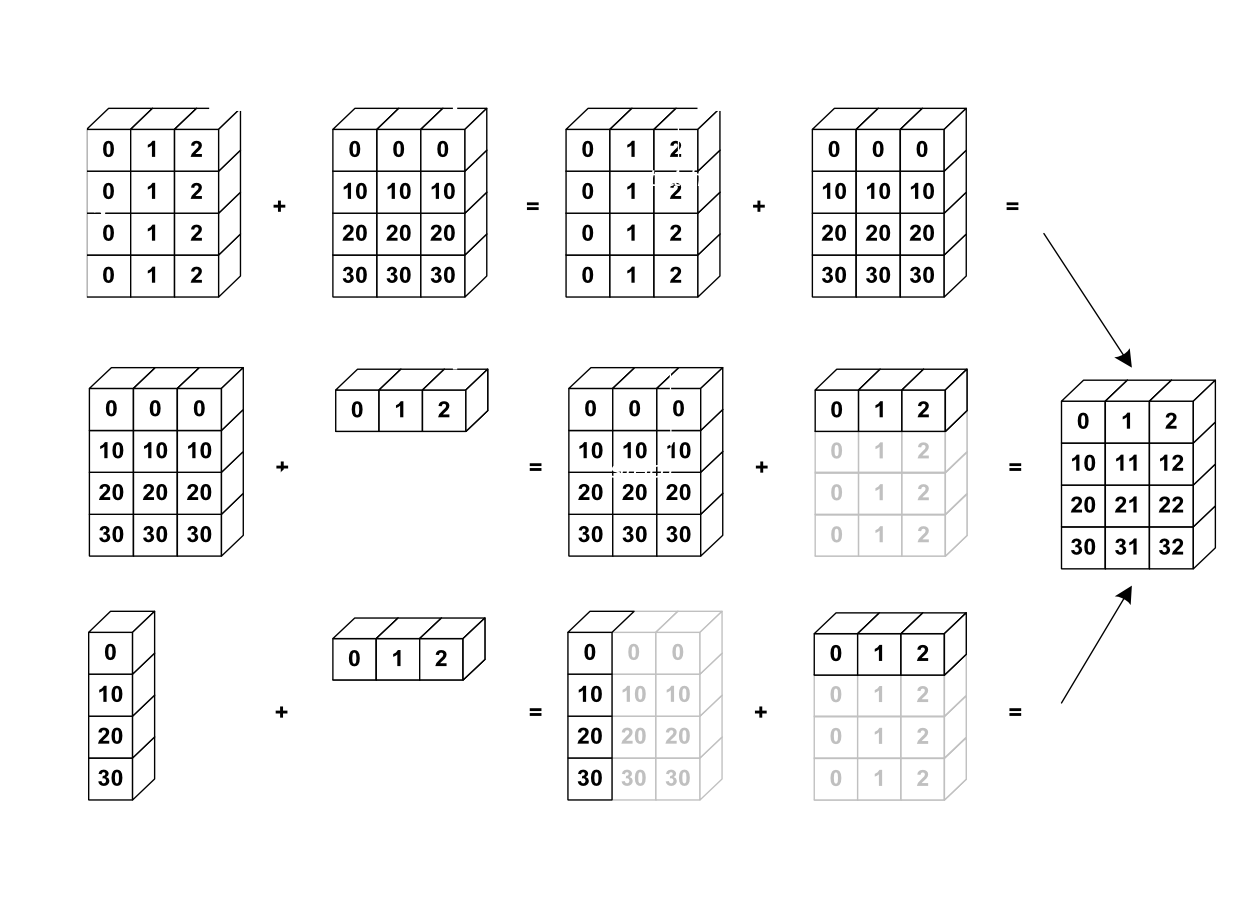
ce qui donne dans Ipython:
>>> a = np.arange(0, 40, 10)
>>> b = np.arange(0, 3)
>>> a = a.reshape((4,1)) #il faut transformer a en tableau "vertical"
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
On a déjà utilisé le broadcasting sans le savoir
>>> a = np.arange(20).reshape((4,5))
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
>>> a[0] = 1 # on égale deux tableaux de dimension 1 et 0
>>> a[:3] = np.arange(1,6)
>>> a
array([[ 1, 2, 3, 4, 5],
[ 1, 2, 3, 4, 5],
[ 1, 2, 3, 4, 5],
[15, 16, 17, 18, 19]])
On peut même utiliser en même temps le fancy indexing et le broadcasting : reprenons un exemple déjà utilisé plus haut
>>> a = np.arange(12).reshape(3,4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> i = np.array( [ [0,1],
... [1,2] ] )
>>> a[i, 2] # même chose que a[i, 2*np.ones((2,2), dtype=int)]
array([[ 2, 6],
[ 6, 10]])
Le broadcasting peut sembler un peu magique, mais il est en fait assez naturel de l’utiliser dès qu’on veut veut résoudre un problème où on obtient en sortie un tableau avec plus de dimensions que les données en entrée.
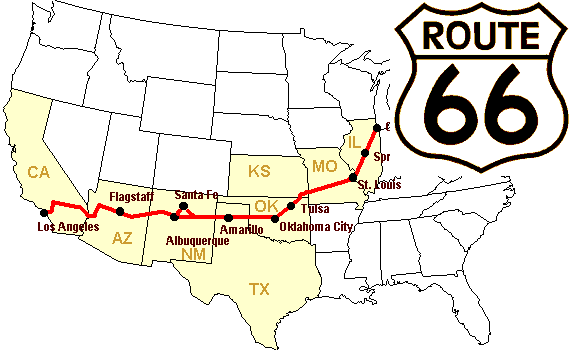
Exemple : construisons un tableau de distances (en miles) entre les villes de la route 66 : Chicago, Springfield, Saint-Louis, Tulsa, Oklahoma City, Amarillo, Santa Fe, Albucquerque, Flagstaff et Los Angeles.
>>> mileposts = np.array([0, 198, 303, 736, 871, 1175, 1475, 1544,
... 1913, 2448])
>>> tableau_de_distances = np.abs(mileposts - mileposts[:,np.newaxis])
>>> tableau_de_distances
array([[ 0, 198, 303, 736, 871, 1175, 1475, 1544, 1913, 2448],
[ 198, 0, 105, 538, 673, 977, 1277, 1346, 1715, 2250],
[ 303, 105, 0, 433, 568, 872, 1172, 1241, 1610, 2145],
[ 736, 538, 433, 0, 135, 439, 739, 808, 1177, 1712],
[ 871, 673, 568, 135, 0, 304, 604, 673, 1042, 1577],
[1175, 977, 872, 439, 304, 0, 300, 369, 738, 1273],
[1475, 1277, 1172, 739, 604, 300, 0, 69, 438, 973],
[1544, 1346, 1241, 808, 673, 369, 69, 0, 369, 904],
[1913, 1715, 1610, 1177, 1042, 738, 438, 369, 0, 535],
[2448, 2250, 2145, 1712, 1577, 1273, 973, 904, 535, 0]])
Warning
Bonnes pratiques
Sur l’exemple précédent, on peut noter quelques bonnes (et mauvaises) pratiques :
- Donner des noms de variables explicites (pas besoin d’un commentaire pour expliquer ce qu’il y a dans la variable).
- Mettre des espaces après les virgules, autour des =, etc. Un certain nombre de règles pour écrire du “beau” code (et surtout, utiliser les mêmes conventions que tout le monde !) sont données par le Style Guide for Python Code et la page Docstring Conventions (pour organiser les messages d’aide).
- Sauf exception (ex : cours pour francophones ?), donner des noms de variables en anglais, et écrire les commentaires en anglais (imaginez récupérer un code commenté en russe...).
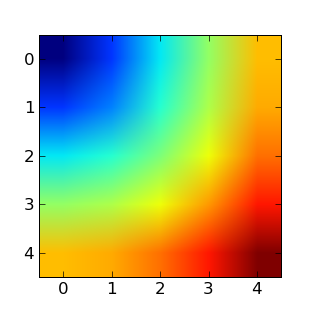
Beaucoup de problèmes sur grille ou réseau peuvent aussi utiliser du broadcasting. Par exemple, si on veut calculer la distance à l’origine des points sur une grille 10x10, on peut faire
>>> x, y = np.arange(5), np.arange(5)
>>> distance = np.sqrt(x**2 + y[:, np.newaxis]**2)
>>> distance
array([[ 0. , 1. , 2. , 3. , 4. ],
[ 1. , 1.41421356, 2.23606798, 3.16227766, 4.12310563],
[ 2. , 2.23606798, 2.82842712, 3.60555128, 4.47213595],
[ 3. , 3.16227766, 3.60555128, 4.24264069, 5. ],
[ 4. , 4.12310563, 4.47213595, 5. , 5.65685425]])
On peut représenter les valeurs du tableau distance en niveau de couleurs grâce à la fonction pylab.imshow (syntaxe : pylab.imshow(distance). voir l’aide pour plus d’options).
Remarque : la fonction numpy.ogrid permet de créer directement les vecteurs x et y de l’exemple précédent avec deux “dimensions significatives” différentes
>>> x, y = np.ogrid[0:5, 0:5]
>>> x, y
(array([[0],
[1],
[2],
[3],
[4]]), array([[0, 1, 2, 3, 4]]))
>>> x.shape, y.shape
((5, 1), (1, 5))
>>> distance = np.sqrt(x**2 + y**2)
np.ogrid est donc très utile dès qu’on a des calculs à faire sur un réseau. np.mgrid fournit par contre directement des matrices pleines d’indices pour les cas où on ne peut/veut pas profiter du broadcasting
>>> x, y = np.mgrid[0:4, 0:4]
>>> x
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
>>> y
array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])
Exercice de synthèse : un médaillon pour Lena¶
Nous allons faire quelques manipulations sur les tableaux numpy en partant de la célébre image de Lena (http://www.cs.cmu.edu/~chuck/lennapg/). scipy fournit un tableau 2D de l’image de Lena avec la fonction scipy.lena
>>> import scipy
>>> lena = scipy.lena()
Voici quelques images que nous allons obtenir grâce à nos manipulations : utiliser différentes colormaps, recadrer l’image, modifier certaines parties de l’image.

- Utilisons la fonction imshow de pylab pour afficher l’image de Lena.
In [3]: import pylab
In [4]: lena = scipy.lena()
In [5]: pylab.imshow(lena)
- Lena s’affiche alors en fausses couleurs, il faut spécifier une colormap pour qu’elle s’affiche en niveaux de gris.
In [6]: pylab.imshow(lena, pl.cm.gray)
In [7]: # ou
In [8]: gray()
- Créez un tableau où le cadrage de Lena est plus serré : enlevez par exemple 30 pixels de tous les côtés de l’image. Affichez ce nouveau tableau avec imshow pour vérifier.
In [9]: crop_lena = lena[30:-30,30:-30]
On veut maintenant entourer le visage de Lena d’un médaillon noir. Pour cela, il faut
- créer un masque correspondant aux pixels qu’on veut mettre en noir. Le masque est défini par la condition (y-256)**2 + (x-256)**2
In [15]: y, x = np.ogrid[0:512,0:512] # les indices x et y des pixels
In [16]: y.shape, x.shape
Out[16]: ((512, 1), (1, 512))
In [17]: centerx, centery = (256, 256) # centre de l'image
In [18]: mask = ((y - centery)**2 + (x - centerx)**2)> 230**2
puis
- affecter la valeur 0 aux pixels de l’image correspondant au masque. La syntaxe pour cela est extrêmement simple et intuitive :
In [19]: lena[mask]=0
In [20]: imshow(lena)
Out[20]: <matplotlib.image.AxesImage object at 0xa36534c>
- Question subsidiaire : recopier toutes les instructions de cet exercice dans un script medaillon_lena.py puis exécuter ce script dans Ipython avec %run medaillon_lena.py.
Conclusion : que faut-il savoir faire sur les tableaux numpy pour démarrer ?
Savoir créer des tableaux : array, arange, ones, zeros.
Connaître la forme du tableau avec array.shape, puis faire du slicing pour obtenir différentes vues du tableau : array[::2], etc. Changer la forme du tableau avec reshape.
Obtenir une partie des éléments d’un tableau et/ou en modifier la valeur grâce aux masques
>>> a[a<0] = 0
Savoir faire quelques opérations sur les tableaux comme trouver le max ou la moyenne (array.max(), array.mean()). Pas la peine de tout retenir, mais avoir le réflexe de chercher dans la doc (voir Savoir chercher (trouver) de l’aide) !!
Pour une utilisation plus avancée : maîtriser l’indexation avec des tableaux d’indices entiers, et le broadcasting. Connaître plus de fonctions de numpy permettant de réaliser des opérations sur les tableaux.