Scipy : le calcul numérique haut-niveau

Scipy

Le module scipy regroupe un certain nombre de sous modules qui sont autant de boîtes à outils de routines courantes de calcul numérique, regroupées par fonction : fonctions spéciales, interpolation, intégration, optimisation, traitement d’images.

Il existe dans le monde du calcul scientifique d’autres bibliothèques standard d’outils de calcul numériques (ex : la GSL - GNU Scientific Library pour les programmes en C/C++, ou les toolboxes de Matlab). Les scientifiques ont trop souvent tendance à oublier leur existence et à réinventer la roue en reprogrammant leur algorithmes d’intégration, d’optimisation, etc. Quand c’est possible, il vaut mieux se servir des outils déjà écrits (testés et optimisés !).

Le type de base en entrée des routines scipy est le tableau numpy.ndarray, ce qui permet d’appliquer ces opérations haut-niveau directement aux tableaux numpy (et de façon très efficace).

Warning

Ce cours n’est pas une introduction aux méthodes de calcul scientifique, et il serait bien ennuyeux d’énumérer une longue liste des différentes fonctions et modules de scipy. On a donc choisi de se concentrer ici sur quelques exemples simples pour donner une idée générale de ce que scipy peut apporter à ses utilisateurs. A chacun ensuite de définir les méthodes numériques dont il a besoin, et de chercher ce qu’il peut utiliser à l’intérieur des sous-modules pertinents.

Pour commencer

>>> import scipy

Fonctions spéciales : scipy.special

Une bibliothèque de fonctions spéciales qu’on retrouve fréquemment. Beaucoup de fonctions courantes sont déjà dans numpy

[In 57]: np.cos, np.sinc, np.tanh
(<ufunc 'cos'>, <function sinc at 0x8adb6bc>, <ufunc 'tanh'>)

il faut chercher les autres dans scipy.special.

Exemple : fonctions de Bessel du premier type

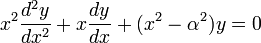
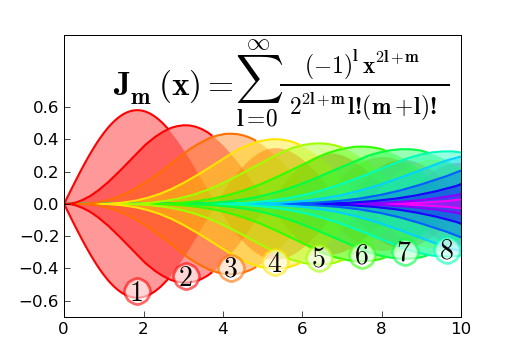
(source : linux mag HS40 http://www.linuxmag-france.org/produit.php?produit=609, Gaël Varoquaux)

>>> from scipy.special import jn
>>> index = 1
>>> x = np.linspace(0, 10, 200)
>>> y = jn(index, x)

Et bien d’autres fonctions : gamma, beta, erf, airy, legendre, fonctions elliptiques, etc.

Algèbre linéaire : scipy.linalg

Les opérations classiques d’algèbre linéaire.

Opérations basiques

>>> from scipy import linalg
>>> a = np.array([[1, 2], [3, 4]])
>>> a = scipy.mat(a) # la transformation tableau -->  matrice est tres simple !
>>> linalg.eigvals(a) # valeurs propres
array([-0.37228132+0.j,  5.37228132+0.j])
>>> linalg.det(a) # determinant
-2.0
>>> a.I # matrice inverse
matrix([[-2. ,  1. ],
        [ 1.5, -0.5]])
>>> linalg.inv(a) # autre ecriture possible
array([[-2. ,  1. ],
       [ 1.5, -0.5]])

... ou moins basiques. Exemple : décomposition en valeurs singulières (SVD)

>>> A = scipy.mat('[1 3 2; 1 2 3]') #matrice non carrée
>>> U,s,Vh = linalg.svd(A)
>>> s # spectre de A
array([ 5.19615242,  1.        ])
>>> print U
[[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]

La SVD est très employée en statistiques ou en traitement du signal.:

>>> l = scipy.lena()
>>> rows, weight, columns = linalg.svd(l, full_matrices=False)
>>> white_lena = np.dot(rows, columns)
>>> weight[20:]=0
>>> W = scipy.mat(linalg.diagsvd(weight,512,512))
>>> filtered_lena = np.dot(rows, np.dot(W, columns))

On trouve dans scipy.linalg bien d’autres décompositions classiques (QR, LU, Cholesky, Schur), des solveurs de systèmes linéaires, etc.

Interpolation : scipy.interpolate

>>> import scipy.interpolate
>>> x = np.linspace(0, 1, 10)
>>> y = np.sin(2*np.pi*x)
>>> linear_interp = scipy.interpolate.interp1d(x, y) #par defaut, interpolateur lineaire
>>> cubic_interp = scipy.interpolate.interp1d(x, y, kind='cubic') #interpolateur cubique
>>> fine_x = np.linspace(0, 1, 50)
>>> y_fromlinearinterp = linear_interp(fine_x)
>>> y_fromcubicinterp = cubic_interp(fine_x)

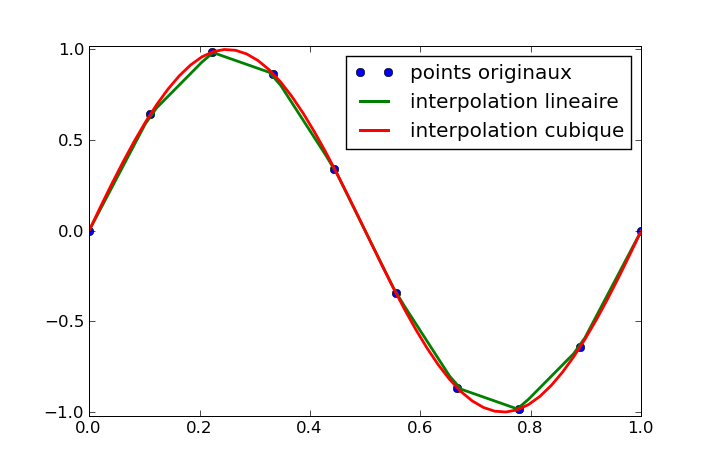
In [246]: plot(x, y, 'o', ms=6, label='points originaux')
Out[246]: [<matplotlib.lines.Line2D object at 0x9ba55ec>]
In [247]: plot(fine_x, y_fromlinearinterp, '-', lw=2,
label='interpolation lineaire')
Out[247]: [<matplotlib.lines.Line2D object at 0xc8300cc>]
In [248]: plot(fine_x, y_fromcubicinterp, '-', lw=2, label='interpolation
cubique')
Out[248]: [<matplotlib.lines.Line2D object at 0xc616b4c>]

Pour des méthodes d’interpolation par splines plus général, voir scipy.interpolate.splrep et scipy.interpolate.splev.

scipy.interpolate.interp2d est similaire à interp1d, pour des tableaux 2D. (mettre une image ?)

Intégration : scipy.integrate

Différentes routines d’intégration numérique. scipy.integrate.quad est la plus générale

In [92]: from scipy.integrate import quad
In [93]: quad(np.sin, 0, np.pi/2)
Out[93]: (0.99999999999999989, 1.1102230246251564e-14)
In [94]: #erreur très faible (l'erreur souhaitée est un paramètre optionnel de quad)
In [95]: 1 - Out[93][0]
Out[95]: 1.1102230246251565e-16

mais il en existe d’autres dans ce sous-module.

Equations différentielles ordinaires (ODE)

Dans ce sous-module, on trouve également un solveur d’équations différentielles ordinaires, scipy.integrate.odeint. Il s’agit d’un solveur générique assez sophistiqué, adapté pour les problèmes raides (stiff en anglais) ou non raides. odeint résout des systèmes d’ODE du premier ordre de la forme

dy1/dt = rhs1(y1, y2, .., t0,...)

dy2/dt = rhs2(y1, y2, .., t0,...)

...

Exemple : résolvons l’ODE dy/dt = -2y entre t=0..10, pour y(t=0)=1.:

>>> from scipy.integrate import odeint
>>> def rhs(y, t): #second membre de l'equa diff
...     return -2*y
...
>>> t = np.linspace(0, 10, 100)
>>> y = odeint(rhs, 1, t) # solution

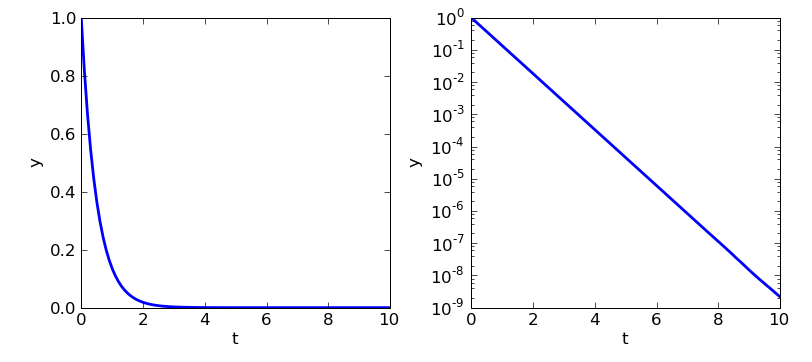
In [344]: plot(t, y)
Out[344]: [<matplotlib.lines.Line2D object at 0xcffaa6c>]
In [345]: clf()
In [346]: semilogy(t, y)
Out[346]: [<matplotlib.lines.Line2D object at 0xd0eebec>]

Exemple : oscillation amortie d’une masse au bout d’un ressort (ODE du 2è ordre)

La position de la masse obéit à l’ODE y'' + nu y' + om^2 y = 0, que l’on peut transformer en un système de deux équations différentielles du premier ordre, en résolvant pour le vecteur Y=(y, y').

>>> def rhs(y,t, om, nu):
...     return (y[1], -om**2*y[0] - nu*y[1])
...
>>> y = odeint(rhs, (1, 0), t, args=(3, 1)) # args correspond à (om, nu)

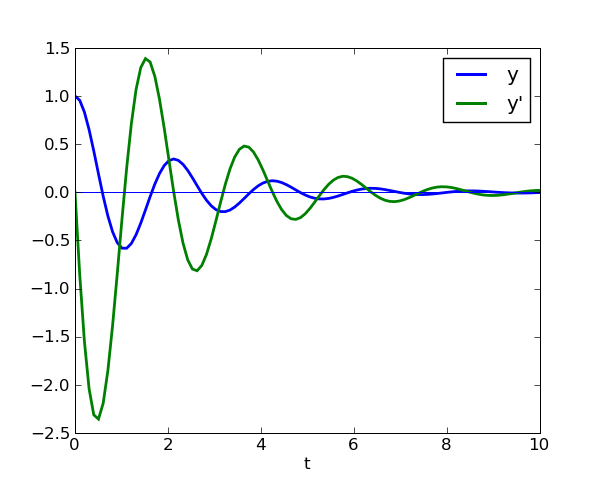
In [385]: plot(t, y[:,0], lw=2, label="y")
Out[385]: [<matplotlib.lines.Line2D object at 0xd675e2c>]
In [386]: plot(t, y[:,1], lw=2, label="y'")
Out[386]: [<matplotlib.lines.Line2D object at 0xd67908c>]
In [387]: legend()
Out[387]: <matplotlib.legend.Legend object at 0xd67e26c>

EDP

Pour les EDP il n’y a pas de solver dans scipy. Il existe néanmoins des packages de solvers d’EDP pour Python, notamment fipy (http://www.ctcms.nist.gov/fipy/).

Optimisation et fit : scipy.optimize

Exemple : simulation d’une marche aléatoire

Reprenons notre exemple de marcheur aléatoire

>>> nreal = 1000 # nombre de réalisations de la marche
>>> tmax = 200 # temps sur lequel on suit le marcheur
>>> # On tire au hasard tous les pas 1 ou -1 de la marche
>>> walk = 2 * ( np.random.random_integers(0, 1, (nreal,200)) - 0.5 )
>>> np.unique(walk) # Vérification : tous les pas font bien 1 ou -1
array([-1.,  1.])
>>> # On construit les marches en sommant ces pas au cours du temps
>>> cumwalk = np.cumsum(walk, axis=1) # axis = 1 : dimension du temps
>>> sq_distance = cumwalk**2
>>> # On moyenne dans le sens des réalisations
>>> mean_distance = np.sqrt(np.mean(sq_distance, axis=0))

On va fitter le tableau mean_distance par une racine carrée.

In [40]: plot(mean_distance)
In [41]: t = np.arange(tmax)
In [42]: def f(A, y, x):
   ....:     """la fonction à optimiser"""
   ....:     err = y - A*np.sqrt(x)
   ....:     return err
   ....:
In [43]: coeff = scipy.optimize.leastsq(f, 0.8, args=(mean_distance, t))
In [44]: coeff
In [45]: coeff
Out[45]: (1.0017300505346165, 3)
In [46]: plot(t, coeff[0]*np.sqrt(t), lw=2)

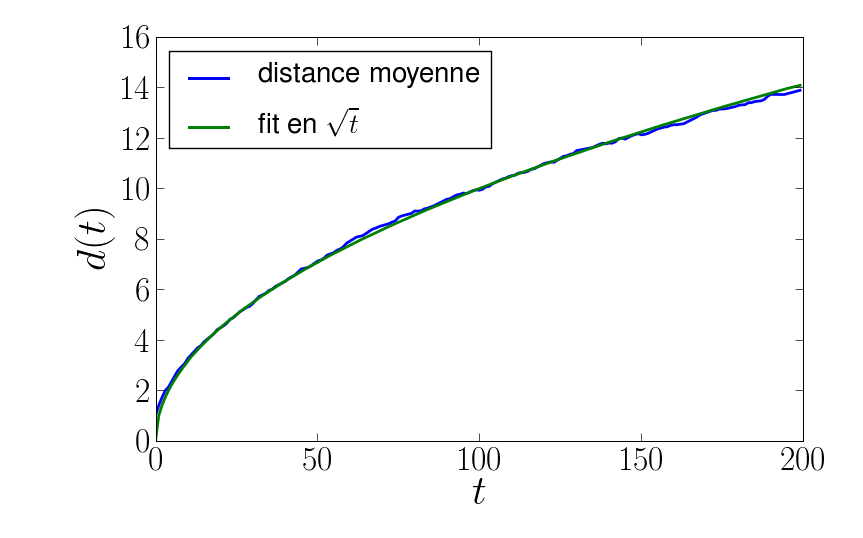
Si on est paresseux on peut dans ce cas-ci se ramener à un fit polynomial

In [47]: t = np.arange(tmax)
In [48]: np.polyfit(t, mean_distance**2, 1)
Out[48]: array([ 1.00452036, -0.08389612])

mais ce n’est pas conseillé, car ce n’est plus le même problème d’optimisation.

Traitement d’images : scipy.ndimage

Ce sous-module propose des routines de traitement d’images à n dimensions (générique pour 2-D, 3-D, etc.).

Un exemple

>>> import scipy.ndimage
>>> lena = scipy.lena()
>>> lena_floue = scipy.ndimage.gaussian_filter(lena, 3)
>>> lena_rotated = scipy.ndimage.rotate(lena, 45)