Project:

Norm-Preserving Fully Discrete Schemes for Micromagnetics

Researcher(s)	:	Prof. Dr. R. Hiptmair
	:	Prof. Dr. Andreas Prohl
Funding	:	no external funding
Duration	:	ongoing project

Description.

We consider the scaled Landau-Lifshitz Gilbert equation for the magnetization ${\mathbf{m}}= (m_{1},m_{2},m_{3})$

$$\frac{d{{\mathbf{m}}}}{dt} = -{\mathbf{m}}\times{\mathbf{h}}_{\ma... ...mathrm{eff}}= -\frac{\partial {\cal E}({\mathbf{m}})}{\partial {\mathbf{m}}}\;,$$ (1)

where the scaled free energy reads

$${\cal E}({\mathbf{m}}) = \tfrac{1}{2}\int\limits_{\Omega}\eta\ver... ...\limits_{\mathbb{R}^{3}}\vert{\mathbf{m}}^{0}\vert^2 \mathrm{d}{\mathbf{x}}\;,$$ (2)

and ${\mathbf{m}}^{0}$ is the $\operatorname{{\bf curl}}$-free component of the $\boldsymbol{L}^2({\mathbb{R}^{3}})$-orthogonal Helmholtz decomposition of ${\mathbf{m}}$:

$${\mathbf{m}}^{0} = \operatorname{{\bf grad}}\psi:\quad \int\limit... ...ad}}\varphi \mathrm{d}{\mathbf{x}}\quad\forall\varphi \in H^1(\mathbb{R}^3)\;.$$

The equations have to be supplied with initial conditions and boundary conditions on $\partial\Omega$.

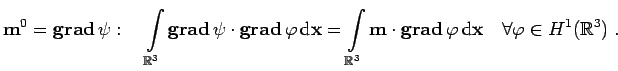During the evolution of (1) the pointwise norm of ${\mathbf{m}}$ is strictly conserved. Moreover, the system has a dissipative nature, which is reflected by the energy decay

$$\frac{d{{\cal E}({\mathbf{m}}(t))}}{dt} = \left<{\frac{\partial {... ...a}\vert{\mathbf{m}}\times{\mathbf{h}}_{\mathrm{eff}}\vert^{2} d{\mathbf{x}}\;.$$

in the case of no excitation.

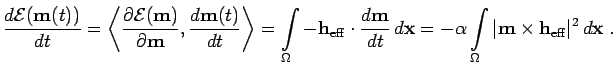A related and simpler evolution problem is the harmonic map heat flowproblem, which describes the gradient flow of the Dirichlet functional for vector fields of unit length. On a given computational domain $\Omega\subset\mathbb{R}^{2}$ and for a given period of time $]0,T[$, $T>0$, this results in the following evolution equations for ${\mathbf{m}}= {\mathbf{m}}(t,{\mathbf{x}}) : ]0,T[\times\Omega\mapsto\mathbb{R}^{3}$:

$$\begin{gather*}\begin{aligned}\frac{\partial {\mathbf{m}}}{\partial t} & = {\mat... ...}}} &= 0 \quad\text{on }]0,T[\times \partial\Omega\;. \end{aligned}\end{gather*}$$ (3)

Goals.

For (3) and (1) we aim to find fully space-time discrete evolution schemes that

1. exactly preserve the modulus of ${\mathbf{m}}$
2. are dissipative in the sense that a suitable discrete energy decays monotonically, if there is no excitation.

Such schemes are already available and arise from combining Runge-Kutta-Gauss timestepping with a mixed discretization in space [SCMW03]. However, no convergence theory has been established for these schemes, not even, if we assume strong solutions of the underlying equations.

The following plots (by P. Corboz) show the computed evolution of ${\mathbf{m}}$ in a particular case. We observe the formation of vortices, which finally disappear at the upper left and the lower right corners. In the final state, the elementary magnets tend to point in the same direction.

Activities. Two term projects are related to this project:

• Philippe Corboz (SS 2003, finished) Mixed implicit timestepping for micromagnetism
• Gian-Marco Baschera and Nicolas Hodler (WS 04/05, ongoing), Parallel numerical schemes for harmonic map heat flow