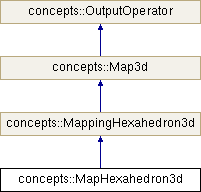
concepts::MapHexahedron3d Class Reference
A 3D element map for a hexahedron. More...
#include <elementMaps3D.hh>
Public Member Functions | |
| MapHexahedron3d * | clone () const |
| Returns a copy of the map. More... | |
| MappingQuad3d * | face (uint face) const |
| Returns the mapping of the given face. More... | |
| MapReal3d | hessian (uint i, const Real x, const Real y, const Real z) const |
| Returns the hessian of the element map. More... | |
| MapReal3d | jacobian (const Real x, const Real y, const Real z) const |
| Returns the jacobian of the element map. More... | |
| Real | jacobianDeterminant (const Real x, const Real y, const Real z) const |
| Returns the determinant of the Jacobian. More... | |
| MapReal3d | jacobianInverse (const Real x, const Real y, const Real z) const |
| Computes the inverse of the jacobian: More... | |
| MapHexahedron3d (char *map, Real scX, Real scY, Real scZ) | |
| Constructor. More... | |
| MapHexahedron3d (const MapHexahedron3d &map) | |
| Copy constructor. More... | |
| MapHexahedron3d (const Real3d &vtx0, const Real3d &vtx1, const Real3d &vtx2, const Real3d &vtx3, const Real3d &vtx4, const Real3d &vtx5, const Real3d &vtx6, const Real3d &vtx7) | |
| Constructor. More... | |
| Real3d | operator() (Real x, Real y, Real z) const |
| Returns a point in 3D mapped from the unit cube | |
| MapHexahedron3d * | part (const Real3d x0, const Real3d z0) const |
| Returns a part of the mapping. More... | |
| ~MapHexahedron3d () | |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. More... | |
Private Member Functions | |
| void | operator= (const MapHexahedron3d &) |
| Private assignement operator. More... | |
Private Attributes | |
| Real3d * | comp_ |
| Computed map. More... | |
| uchar * | map_ |
| Parsed formula for the map. More... | |
| Real | scx_ |
| Right border of the x parameter domain. More... | |
| Real | scy_ |
| Right border of the y parameter domain. More... | |
| Real | scz_ |
| Right border of the z parameter domain. More... | |
| uint | sz_ |
| Length of the parsed formula. More... | |
Detailed Description
A 3D element map for a hexahedron.
The reference element is the unit cube.
There are two ways to fix the map of the hexahedron: give the mapping explicitly or give the eight corners and the map is computed internally.
When giving the eight corners of the hexahedron, they must be given in the correct order, ie. first the corners of the floor (in right screwed orientation pointing into the hexahedron) and then the corners of the ceiling (in right screwed orientation pointing out of the hexahedron).
The application operator maps a point from the unit square onto the physical domain taking into account the parameter domain given in the constructor.
- Examples
- meshes.cc.
Definition at line 366 of file elementMaps3D.hh.
Constructor & Destructor Documentation
◆ MapHexahedron3d() [1/3]
Constructor.
The values of scX, scY and scZ are only for the map, they are not needed by the user for mapping a point from the reference element onto the Real element.
- Parameters
-
map The element map for this hexahedron as a string, x, y and z are the allowed variables, the component are separated by a comma. scX The range of x is [0, scX]. scY The range of y is [0, scY]. scZ The range of z is [0, scZ].
◆ MapHexahedron3d() [2/3]
| concepts::MapHexahedron3d::MapHexahedron3d | ( | const Real3d & | vtx0, |
| const Real3d & | vtx1, | ||
| const Real3d & | vtx2, | ||
| const Real3d & | vtx3, | ||
| const Real3d & | vtx4, | ||
| const Real3d & | vtx5, | ||
| const Real3d & | vtx6, | ||
| const Real3d & | vtx7 | ||
| ) |
Constructor.
Takes the eight physical corners of the hexahedron and computes the element map: ![]() with
with ![]() , where
, where ![]() and
and ![]() .
.
◆ MapHexahedron3d() [3/3]
| concepts::MapHexahedron3d::MapHexahedron3d | ( | const MapHexahedron3d & | map | ) |
Copy constructor.
◆ ~MapHexahedron3d()
|
inline |
Definition at line 416 of file elementMaps3D.hh.
Member Function Documentation
◆ clone()
|
inlinevirtual |
Returns a copy of the map.
Implements concepts::MappingHexahedron3d.
Definition at line 472 of file elementMaps3D.hh.
◆ face()
|
virtual |
Returns the mapping of the given face.
Implements concepts::MappingHexahedron3d.
◆ hessian()
|
virtual |
Returns the hessian of the element map.
Implements concepts::MappingHexahedron3d.
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Implements concepts::MappingHexahedron3d.
◆ jacobian()
◆ jacobianDeterminant()
|
inlinevirtual |
Returns the determinant of the Jacobian.
Reimplemented from concepts::MappingHexahedron3d.
Definition at line 467 of file elementMaps3D.hh.
◆ jacobianInverse()
|
inlinevirtual |
Computes the inverse of the jacobian:
![]()
Reimplemented from concepts::MappingHexahedron3d.
Definition at line 462 of file elementMaps3D.hh.
◆ operator()()
Returns a point in 3D mapped from the unit cube ![]() onto the element in the original mesh.
onto the element in the original mesh.
- Returns
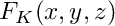
- Parameters
-
x ![$\in [0, 1]$](form_382.png)
y ![$\in [0, 1]$](form_382.png)
z ![$\in [0, 1]$](form_382.png)
Implements concepts::MappingHexahedron3d.
Definition at line 426 of file elementMaps3D.hh.
◆ operator=()
|
private |
Private assignement operator.
◆ part()
|
virtual |
Returns a part of the mapping.
Implements concepts::MappingHexahedron3d.
Member Data Documentation
◆ comp_
|
private |
Computed map.
Definition at line 384 of file elementMaps3D.hh.
◆ map_
|
private |
Parsed formula for the map.
Definition at line 369 of file elementMaps3D.hh.
◆ scx_
|
private |
Right border of the x parameter domain.
Definition at line 375 of file elementMaps3D.hh.
◆ scy_
|
private |
Right border of the y parameter domain.
Definition at line 378 of file elementMaps3D.hh.
◆ scz_
|
private |
Right border of the z parameter domain.
Definition at line 381 of file elementMaps3D.hh.
◆ sz_
|
private |
Length of the parsed formula.
Definition at line 372 of file elementMaps3D.hh.
The documentation for this class was generated from the following file:
- geometry/elementMaps3D.hh

