meshes.cc

In this tutorial, meshes in one, two and three dimensions are shown. This tutorial does not describe a program which can be used to generate an executable. Therefore, there is no need to type make meshes

The following meshes are included:

  1. Mesh in One Dimension: Line
  2. Meshes in Two Dimensions: LshapedTriangle, LshapedQuad
  3. Mesh in Three Dimensions: LshapedCube

Mesh in One Dimension

Line

The mesh is the interval from 1 to 5 with two cells. One is (1,2) and the other is (2,5). They are coupled in the class Line which makes it possible to loop over the cells.

class Line : public concepts::Mesh1 {
public:
Line(Real left = 1.0, Real mid = 2.0, Real right = 5.0);
virtual ~Line();
unsigned int ncell() const { return 2; }
concepts::Scan1* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[3];
concepts::Edge *edg_[2];
concepts::Cell1 *cell_[2];

A scanner is used to loop over all cells in a mesh. S is the scanner for this mesh. It is used in the constructor of the space to create the elements on the cells of the mesh. With the ++ operator it is possible to loop over the cells of the mesh. The constructor of the space shows an example of the usage of a scanner and its ++ operator.

class S : public concepts::Scan<concepts::Cell1> {
unsigned int idx_;
concepts::Cell1 *(&cell_)[2];
public:
S(concepts::Cell1 *(&cell)[2]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 2; }
concepts::Cell1& operator++(int) { return *cell_[idx_++]; }
concepts::Scan1* clone() const { return new S(*this); }
};
};

The constructor of the mesh Line sets up everything which is needed:

Line::Line(Real left, Real mid, Real right) {
  1. the vertices
    vtx_[0] = new concepts::Vertex(2);
    vtx_[1] = new concepts::Vertex(0);
    vtx_[2] = new concepts::Vertex(2);
  2. the edges (they share the middle vertex)
    edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1]);
    edg_[1] = new concepts::Edge(*vtx_[1], *vtx_[2]);
  3. and the cells which live on the edges. Here, the element map is given.
    cell_[0] = new concepts::Edge1d(*edg_[0], concepts::MapEdge1d(left, mid));
    cell_[1] = new concepts::Edge1d(*edg_[1], concepts::MapEdge1d(mid, right));
    }

The destructor of the mesh removes all components which where created in the constructor.

Line::~Line() {
for (int i = 0; i < 2; ++i)
delete cell_[i];
for (int i = 0; i < 2; ++i)
delete edg_[i];
for (int i = 0; i < 3; ++i)
delete vtx_[i];
}

The info member prints the two cells of the mesh. It is used by the output operator of the base class concepts::OutputOperator.

std::ostream& Line::info(std::ostream& os) const {
os << "Line(" << *cell_[0] << ", " << *cell_[1] << ')';
return os;
}

Meshes in Two Dimensions

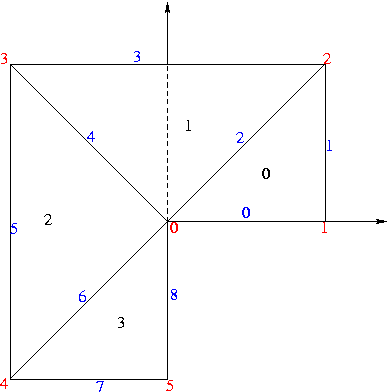
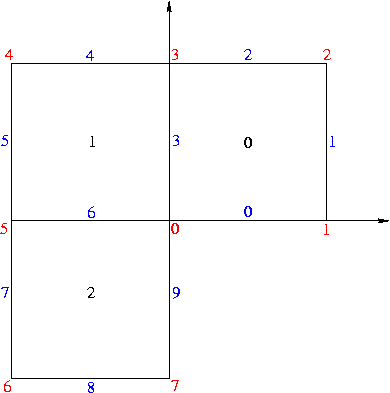
L Shaped Domain in Triangles

L shaped domain

The mesh is the L shaped domain (-1,1)2 \ (0,1) x (-1,0) as shown in the figure above. The red numbers denote the vertices, the blue numbers the edges and the black numbers the cells and triangles.

class LshapedTriangle : public concepts::Mesh2 {
public:
LshapedTriangle();
virtual ~LshapedTriangle();
unsigned int ncell() const { return 4; }
concepts::Scan2* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[6];
concepts::Edge *edg_[9];
concepts::Triangle *tri_[4];
concepts::Cell2 *cell_[4];
class S : public concepts::Scan<concepts::Cell2> {
unsigned int idx_;
concepts::Cell2 *(&cell_)[4];
public:
S(concepts::Cell2 *(&cell)[4]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 4; }
concepts::Cell2& operator++(int) { return *cell_[idx_++]; }
concepts::Scan2* clone() const { return new S(*this); }
};
};
LshapedTriangle::LshapedTriangle() {
for (uint i = 0; i < 6; ++i)
vtx_[i] = new concepts::Vertex();

The order of the vertices in the constructor of the edge does not matter. Every edge on the boundary of the domain gets a unique number. This number is used to identify the edge when specifying boundary conditions. 0 is reserved for free edges (and is the default) and should therefore not be used to specify a bounary condition.

edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[0], *vtx_[2]);
edg_[3] = new concepts::Edge(*vtx_[2], *vtx_[3], 3);
edg_[4] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[5] = new concepts::Edge(*vtx_[3], *vtx_[4], 4);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[4]);
edg_[7] = new concepts::Edge(*vtx_[4], *vtx_[5], 5);
edg_[8] = new concepts::Edge(*vtx_[0], *vtx_[5], 6);

The order of the edges matters: they must be listed counterclockwise.

tri_[0] = new concepts::Triangle(*edg_[0], *edg_[1], *edg_[2]);
tri_[1] = new concepts::Triangle(*edg_[2], *edg_[3], *edg_[4]);
tri_[2] = new concepts::Triangle(*edg_[4], *edg_[5], *edg_[6]);
tri_[3] = new concepts::Triangle(*edg_[6], *edg_[7], *edg_[8]);

The element map is given by the three vertices beginning with the vertices of the first edge from the construction of the triangle. As for the edges, the vertices have to be ordered counterclockwise.

cell_[0] = new concepts::Triangle2d
(*tri_[0], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(1.0, 0.0),
concepts::Real2d(1.0, 1.0)));
cell_[1] = new concepts::Triangle2d
(*tri_[1], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(1.0, 1.0),
concepts::Real2d(-1.0, 1.0)));
cell_[2] = new concepts::Triangle2d
(*tri_[2], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(-1.0, 1.0),
concepts::Real2d(-1.0, -1.0)));
cell_[3] = new concepts::Triangle2d
(*tri_[3], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(-1.0, -1.0),
concepts::Real2d(0.0, -1.0)));
}
LshapedTriangle::~LshapedTriangle() {
for (int i = 0; i < 4; ++i)
delete cell_[i];
for (int i = 0; i < 4; ++i)
delete tri_[i];
for (int i = 0; i < 9; ++i)
delete edg_[i];
for (int i = 0; i < 6; ++i)
delete vtx_[i];
}
std::ostream& LshapedTriangle::info(std::ostream& os) const {
os << "LshapedTriangle(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ", " << *cell_[3] << ')';
return os;
}

L Shaped Domain in Quadrilaterals

L shaped domain

The mesh is the L shaped domain (-1,1)2 \ (0,1) x (-1,0) as shown in the figure above. The red numbers denote the vertices, the blue numbers the edges and the black numbers the cells and triangles.

class LshapedQuad : public concepts::Mesh2 {
public:
LshapedQuad();
virtual ~LshapedQuad();
unsigned int ncell() const { return 3; }
concepts::Scan2* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[8];
concepts::Edge *edg_[10];
concepts::Quad *quad_[3];
concepts::Cell2 *cell_[3];
class S : public concepts::Scan<concepts::Cell2> {
unsigned int idx_;
concepts::Cell2 *(&cell_)[3];
public:
S(concepts::Cell2 *(&cell)[3]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 3; }
concepts::Cell2& operator++(int) { return *cell_[idx_++]; }
concepts::Scan2* clone() const { return new S(*this); }
};
};
LshapedQuad::LshapedQuad() {
for (uint i = 0; i < 8; ++i)
vtx_[i] = new concepts::Vertex();
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[3], *vtx_[2], 3);
edg_[3] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[4] = new concepts::Edge(*vtx_[4], *vtx_[3], 4);
edg_[5] = new concepts::Edge(*vtx_[5], *vtx_[4], 5);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[5]);
edg_[7] = new concepts::Edge(*vtx_[6], *vtx_[5], 6);
edg_[8] = new concepts::Edge(*vtx_[6], *vtx_[7], 7);
edg_[9] = new concepts::Edge(*vtx_[0], *vtx_[7], 8);
quad_[0] = new concepts::Quad(*edg_[0], *edg_[1], *edg_[2], *edg_[3]);
quad_[1] = new concepts::Quad(*edg_[3], *edg_[4], *edg_[5], *edg_[6]);
quad_[2] = new concepts::Quad(*edg_[6], *edg_[7], *edg_[8], *edg_[9]);

The element map is given by the 2D map of the unit square [0,1]2 onto the element.

cell_[0] = new concepts::Quad2d(*quad_[0],
concepts::MapQuad2d("(x,y)", 1.0, 1.0));
cell_[1] = new concepts::Quad2d(*quad_[1],
concepts::MapQuad2d("(-y,x)", 1.0, 1.0));
cell_[2] = new concepts::Quad2d(*quad_[2],
concepts::MapQuad2d("(-x,-y)", 1.0, 1.0));
}
LshapedQuad::~LshapedQuad() {
for (int i = 0; i < 3; ++i)
delete cell_[i];
for (int i = 0; i < 3; ++i)
delete quad_[i];
for (int i = 0; i < 10; ++i)
delete edg_[i];
for (int i = 0; i < 8; ++i)
delete vtx_[i];
}
std::ostream& LshapedQuad::info(std::ostream& os) const {
os << "LshapedQuad(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ')';
return os;
}

Meshes in Three Dimensions

Thick L Shaped Domain

The mesh is the thick L shaped domain (-1,1)2 x (0,1) \ (0,1) x (-1,0) x (0,1).

class LshapedCube : public concepts::Mesh3 {
public:
LshapedCube();
virtual ~LshapedCube();
unsigned int ncell() const { return 3; }
concepts::Scan3* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
class S : public concepts::Scan<concepts::Cell3> {
unsigned int idx_;
concepts::Hexahedron3d *(&cell_)[3];
public:
S(concepts::Hexahedron3d *(&cell)[3]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 3; }
concepts::Cell3& operator++(int) { return *cell_[idx_++]; }
concepts::Scan3* clone() const { return new S(*this); }
};
concepts::Vertex *vtx_[16];
concepts::Edge *edg_[28];
concepts::Quad *quad_[16];
concepts::Hexahedron *hex_[3];
concepts::Hexahedron3d *cell_[3];
};
LshapedCube::LshapedCube() {
for (uint i = 0; i < 16; ++i)
vtx_[i] = new concepts::Vertex();
// edges in the ground surface
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[3], *vtx_[2], 3);
edg_[3] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[4] = new concepts::Edge(*vtx_[4], *vtx_[3], 4);
edg_[5] = new concepts::Edge(*vtx_[5], *vtx_[4], 5);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[5]);
edg_[7] = new concepts::Edge(*vtx_[6], *vtx_[5], 6);
edg_[8] = new concepts::Edge(*vtx_[6], *vtx_[7], 7);
edg_[9] = new concepts::Edge(*vtx_[0], *vtx_[7], 8);
// edges in the top surface
edg_[10] = new concepts::Edge(*vtx_[8], *vtx_[9], 9);
edg_[11] = new concepts::Edge(*vtx_[10], *vtx_[9], 10);
edg_[12] = new concepts::Edge(*vtx_[11], *vtx_[10], 11);
edg_[13] = new concepts::Edge(*vtx_[8], *vtx_[11]);
edg_[14] = new concepts::Edge(*vtx_[12], *vtx_[11], 12);
edg_[15] = new concepts::Edge(*vtx_[13], *vtx_[12], 13);
edg_[16] = new concepts::Edge(*vtx_[8], *vtx_[13]);
edg_[17] = new concepts::Edge(*vtx_[14], *vtx_[13], 14);
edg_[18] = new concepts::Edge(*vtx_[14], *vtx_[15], 15);
edg_[19] = new concepts::Edge(*vtx_[8], *vtx_[15], 16);
// edges on the side surfaces
edg_[20] = new concepts::Edge(*vtx_[0], *vtx_[8], 17);
edg_[21] = new concepts::Edge(*vtx_[1], *vtx_[9], 18);
edg_[22] = new concepts::Edge(*vtx_[2], *vtx_[10], 19);
edg_[23] = new concepts::Edge(*vtx_[3], *vtx_[11], 20);
edg_[24] = new concepts::Edge(*vtx_[4], *vtx_[12], 21);
edg_[25] = new concepts::Edge(*vtx_[5], *vtx_[13], 22);
edg_[26] = new concepts::Edge(*vtx_[6], *vtx_[14], 23);
edg_[27] = new concepts::Edge(*vtx_[7], *vtx_[15], 24);
// quadrilaterals on the ground surface
quad_[0] = new concepts::Quad(*edg_[0], *edg_[1], *edg_[2], *edg_[3]);
DEBUGL(1, "0");
quad_[1] = new concepts::Quad(*edg_[3], *edg_[4], *edg_[5], *edg_[6]);
DEBUGL(1, "1");
quad_[2] = new concepts::Quad(*edg_[6], *edg_[7], *edg_[8], *edg_[9]);
DEBUGL(1, "2");
// quadrilaterals on the top surface
quad_[3] = new concepts::Quad(*edg_[10], *edg_[11], *edg_[12], *edg_[13]);
DEBUGL(1, "3");
quad_[4] = new concepts::Quad(*edg_[13], *edg_[14], *edg_[15], *edg_[16]);
DEBUGL(1, "4");
quad_[5] = new concepts::Quad(*edg_[16], *edg_[17], *edg_[18], *edg_[19]);
DEBUGL(1, "5");
// quadrilaterals on the side surfaces
quad_[6] = new concepts::Quad(*edg_[0], *edg_[21], *edg_[10], *edg_[20]);
DEBUGL(1, "6");
quad_[7] = new concepts::Quad(*edg_[1], *edg_[22], *edg_[11], *edg_[21]);
DEBUGL(1, "7");
quad_[8] = new concepts::Quad(*edg_[2], *edg_[23], *edg_[12], *edg_[22]);
DEBUGL(1, "8");
quad_[9] = new concepts::Quad(*edg_[4], *edg_[24], *edg_[14], *edg_[23]);
DEBUGL(1, "9");
quad_[10] = new concepts::Quad(*edg_[5], *edg_[25], *edg_[15], *edg_[24]);
DEBUGL(1, "10");
quad_[11] = new concepts::Quad(*edg_[7], *edg_[26], *edg_[17], *edg_[25]);
DEBUGL(1, "11");
quad_[12] = new concepts::Quad(*edg_[8], *edg_[27], *edg_[18], *edg_[26]);
DEBUGL(1, "12");
quad_[13] = new concepts::Quad(*edg_[9], *edg_[20], *edg_[19], *edg_[27]);
DEBUGL(1, "13");
// inner quadrilaterals
quad_[14] = new concepts::Quad(*edg_[3], *edg_[23], *edg_[13], *edg_[20]);
DEBUGL(1, "14");
quad_[15] = new concepts::Quad(*edg_[6], *edg_[25], *edg_[16], *edg_[20]);
DEBUGL(1, "15");
hex_[0] = new concepts::Hexahedron(*quad_[0], *quad_[6], *quad_[7],
*quad_[8], *quad_[14], *quad_[3]);
hex_[1] = new concepts::Hexahedron(*quad_[1], *quad_[15], *quad_[14],
*quad_[9], *quad_[10], *quad_[4]);
hex_[2] = new concepts::Hexahedron(*quad_[2], *quad_[12], *quad_[13],

The element map is given by the 3D map of the unit cube [0,1]3 onto the element.

cell_[0] = new concepts::Hexahedron3d
(*hex_[0],
concepts::MapHexahedron3d(concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(1.0, 0.0, 0.0),
concepts::Real3d(1.0, 1.0, 0.0),
concepts::Real3d(0.0, 1.0, 0.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(1.0, 0.0, 1.0),
concepts::Real3d(1.0, 1.0, 1.0),
concepts::Real3d(0.0, 1.0, 1.0))
);
cell_[1] = new concepts::Hexahedron3d
(*hex_[1],
concepts::MapHexahedron3d(concepts::Real3d(-1.0, 0.0, 0.0),
concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(0.0, 1.0, 0.0),
concepts::Real3d(-1.0, 1.0, 0.0),
concepts::Real3d(-1.0, 0.0, 1.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(0.0, 1.0, 1.0),
concepts::Real3d(-1.0, 1.0, 1.0))
);
cell_[2] = new concepts::Hexahedron3d
(*hex_[2],
concepts::MapHexahedron3d(concepts::Real3d(-1.0, -1.0, 0.0),
concepts::Real3d(0.0, -1.0, 0.0),
concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(-1.0, 0.0, 0.0),
concepts::Real3d(-1.0, -1.0, 1.0),
concepts::Real3d(0.0, -1.0, 1.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(-1.0, 0.0, 1.0))
);
}
LshapedCube::~LshapedCube() {
for (int i = 0; i < 3; ++i)
delete cell_[i];
for (int i = 0; i < 3; ++i)
delete hex_[i];
for (int i = 0; i < 16; ++i)
delete quad_[i];
for (int i = 0; i < 28; ++i)
delete edg_[i];
for (int i = 0; i < 16; ++i)
delete vtx_[i];
}
std::ostream& LshapedCube::info(std::ostream& os) const {
os << "LshapedCube(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ')';
return os;
}

Complete Source Code

Author
Philipp Frauenfelder, 2004
// ******************************************************************** Line **
class Line : public concepts::Mesh1 {
public:
Line(Real left = 1.0, Real mid = 2.0, Real right = 5.0);
virtual ~Line();
unsigned int ncell() const { return 2; }
concepts::Scan1* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[3];
concepts::Edge *edg_[2];
concepts::Cell1 *cell_[2];
class S : public concepts::Scan<concepts::Cell1> {
unsigned int idx_;
concepts::Cell1 *(&cell_)[2];
public:
S(concepts::Cell1 *(&cell)[2]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 2; }
concepts::Cell1& operator++(int) { return *cell_[idx_++]; }
concepts::Scan1* clone() const { return new S(*this); }
};
};
Line::Line(Real left, Real mid, Real right) {
vtx_[0] = new concepts::Vertex(2);
vtx_[1] = new concepts::Vertex(0);
vtx_[2] = new concepts::Vertex(2);
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1]);
edg_[1] = new concepts::Edge(*vtx_[1], *vtx_[2]);
cell_[0] = new concepts::Edge1d(*edg_[0], concepts::MapEdge1d(left, mid));
cell_[1] = new concepts::Edge1d(*edg_[1], concepts::MapEdge1d(mid, right));
}
Line::~Line() {
for (int i = 0; i < 2; ++i)
delete cell_[i];
for (int i = 0; i < 2; ++i)
delete edg_[i];
for (int i = 0; i < 3; ++i)
delete vtx_[i];
}
std::ostream& Line::info(std::ostream& os) const {
os << "Line(" << *cell_[0] << ", " << *cell_[1] << ')';
return os;
}
// ******************************************************************** Mesh **
class LshapedTriangle : public concepts::Mesh2 {
public:
LshapedTriangle();
virtual ~LshapedTriangle();
unsigned int ncell() const { return 4; }
concepts::Scan2* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[6];
concepts::Edge *edg_[9];
concepts::Triangle *tri_[4];
concepts::Cell2 *cell_[4];
class S : public concepts::Scan<concepts::Cell2> {
unsigned int idx_;
concepts::Cell2 *(&cell_)[4];
public:
S(concepts::Cell2 *(&cell)[4]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 4; }
concepts::Cell2& operator++(int) { return *cell_[idx_++]; }
concepts::Scan2* clone() const { return new S(*this); }
};
};
LshapedTriangle::LshapedTriangle() {
for (uint i = 0; i < 6; ++i)
vtx_[i] = new concepts::Vertex();
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[0], *vtx_[2]);
edg_[3] = new concepts::Edge(*vtx_[2], *vtx_[3], 3);
edg_[4] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[5] = new concepts::Edge(*vtx_[3], *vtx_[4], 4);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[4]);
edg_[7] = new concepts::Edge(*vtx_[4], *vtx_[5], 5);
edg_[8] = new concepts::Edge(*vtx_[0], *vtx_[5], 6);
tri_[0] = new concepts::Triangle(*edg_[0], *edg_[1], *edg_[2]);
tri_[1] = new concepts::Triangle(*edg_[2], *edg_[3], *edg_[4]);
tri_[2] = new concepts::Triangle(*edg_[4], *edg_[5], *edg_[6]);
tri_[3] = new concepts::Triangle(*edg_[6], *edg_[7], *edg_[8]);
cell_[0] = new concepts::Triangle2d
(*tri_[0], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(1.0, 0.0),
concepts::Real2d(1.0, 1.0)));
cell_[1] = new concepts::Triangle2d
(*tri_[1], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(1.0, 1.0),
concepts::Real2d(-1.0, 1.0)));
cell_[2] = new concepts::Triangle2d
(*tri_[2], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(-1.0, 1.0),
concepts::Real2d(-1.0, -1.0)));
cell_[3] = new concepts::Triangle2d
(*tri_[3], concepts::VertexTriangle2d(concepts::Real2d(0.0, 0.0),
concepts::Real2d(-1.0, -1.0),
concepts::Real2d(0.0, -1.0)));
}
LshapedTriangle::~LshapedTriangle() {
for (int i = 0; i < 4; ++i)
delete cell_[i];
for (int i = 0; i < 4; ++i)
delete tri_[i];
for (int i = 0; i < 9; ++i)
delete edg_[i];
for (int i = 0; i < 6; ++i)
delete vtx_[i];
}
std::ostream& LshapedTriangle::info(std::ostream& os) const {
os << "LshapedTriangle(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ", " << *cell_[3] << ')';
return os;
}
// ******************************************************************** Mesh **
class LshapedQuad : public concepts::Mesh2 {
public:
LshapedQuad();
virtual ~LshapedQuad();
unsigned int ncell() const { return 3; }
concepts::Scan2* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
concepts::Vertex *vtx_[8];
concepts::Edge *edg_[10];
concepts::Quad *quad_[3];
concepts::Cell2 *cell_[3];
class S : public concepts::Scan<concepts::Cell2> {
unsigned int idx_;
concepts::Cell2 *(&cell_)[3];
public:
S(concepts::Cell2 *(&cell)[3]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 3; }
concepts::Cell2& operator++(int) { return *cell_[idx_++]; }
concepts::Scan2* clone() const { return new S(*this); }
};
};
LshapedQuad::LshapedQuad() {
for (uint i = 0; i < 8; ++i)
vtx_[i] = new concepts::Vertex();
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[3], *vtx_[2], 3);
edg_[3] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[4] = new concepts::Edge(*vtx_[4], *vtx_[3], 4);
edg_[5] = new concepts::Edge(*vtx_[5], *vtx_[4], 5);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[5]);
edg_[7] = new concepts::Edge(*vtx_[6], *vtx_[5], 6);
edg_[8] = new concepts::Edge(*vtx_[6], *vtx_[7], 7);
edg_[9] = new concepts::Edge(*vtx_[0], *vtx_[7], 8);
quad_[0] = new concepts::Quad(*edg_[0], *edg_[1], *edg_[2], *edg_[3]);
quad_[1] = new concepts::Quad(*edg_[3], *edg_[4], *edg_[5], *edg_[6]);
quad_[2] = new concepts::Quad(*edg_[6], *edg_[7], *edg_[8], *edg_[9]);
cell_[0] = new concepts::Quad2d(*quad_[0],
concepts::MapQuad2d("(x,y)", 1.0, 1.0));
cell_[1] = new concepts::Quad2d(*quad_[1],
concepts::MapQuad2d("(-y,x)", 1.0, 1.0));
cell_[2] = new concepts::Quad2d(*quad_[2],
concepts::MapQuad2d("(-x,-y)", 1.0, 1.0));
}
LshapedQuad::~LshapedQuad() {
for (int i = 0; i < 3; ++i)
delete cell_[i];
for (int i = 0; i < 3; ++i)
delete quad_[i];
for (int i = 0; i < 10; ++i)
delete edg_[i];
for (int i = 0; i < 8; ++i)
delete vtx_[i];
}
std::ostream& LshapedQuad::info(std::ostream& os) const {
os << "LshapedQuad(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ')';
return os;
}
// ******************************************************************** Mesh **
class LshapedCube : public concepts::Mesh3 {
public:
LshapedCube();
virtual ~LshapedCube();
unsigned int ncell() const { return 3; }
concepts::Scan3* scan() { return new S(cell_); }
virtual std::ostream& info(std::ostream& os) const;
private:
class S : public concepts::Scan<concepts::Cell3> {
unsigned int idx_;
concepts::Hexahedron3d *(&cell_)[3];
public:
S(concepts::Hexahedron3d *(&cell)[3]) : idx_(0), cell_(cell) {}
S(const S& scan) : idx_(scan.idx_), cell_(scan.cell_) {}
bool eos() const { return idx_ == 3; }
concepts::Cell3& operator++(int) { return *cell_[idx_++]; }
concepts::Scan3* clone() const { return new S(*this); }
};
concepts::Vertex *vtx_[16];
concepts::Edge *edg_[28];
concepts::Quad *quad_[16];
concepts::Hexahedron *hex_[3];
concepts::Hexahedron3d *cell_[3];
};
LshapedCube::LshapedCube() {
for (uint i = 0; i < 16; ++i)
vtx_[i] = new concepts::Vertex();
// edges in the ground surface
edg_[0] = new concepts::Edge(*vtx_[0], *vtx_[1], 1);
edg_[1] = new concepts::Edge(*vtx_[2], *vtx_[1], 2);
edg_[2] = new concepts::Edge(*vtx_[3], *vtx_[2], 3);
edg_[3] = new concepts::Edge(*vtx_[0], *vtx_[3]);
edg_[4] = new concepts::Edge(*vtx_[4], *vtx_[3], 4);
edg_[5] = new concepts::Edge(*vtx_[5], *vtx_[4], 5);
edg_[6] = new concepts::Edge(*vtx_[0], *vtx_[5]);
edg_[7] = new concepts::Edge(*vtx_[6], *vtx_[5], 6);
edg_[8] = new concepts::Edge(*vtx_[6], *vtx_[7], 7);
edg_[9] = new concepts::Edge(*vtx_[0], *vtx_[7], 8);
// edges in the top surface
edg_[10] = new concepts::Edge(*vtx_[8], *vtx_[9], 9);
edg_[11] = new concepts::Edge(*vtx_[10], *vtx_[9], 10);
edg_[12] = new concepts::Edge(*vtx_[11], *vtx_[10], 11);
edg_[13] = new concepts::Edge(*vtx_[8], *vtx_[11]);
edg_[14] = new concepts::Edge(*vtx_[12], *vtx_[11], 12);
edg_[15] = new concepts::Edge(*vtx_[13], *vtx_[12], 13);
edg_[16] = new concepts::Edge(*vtx_[8], *vtx_[13]);
edg_[17] = new concepts::Edge(*vtx_[14], *vtx_[13], 14);
edg_[18] = new concepts::Edge(*vtx_[14], *vtx_[15], 15);
edg_[19] = new concepts::Edge(*vtx_[8], *vtx_[15], 16);
// edges on the side surfaces
edg_[20] = new concepts::Edge(*vtx_[0], *vtx_[8], 17);
edg_[21] = new concepts::Edge(*vtx_[1], *vtx_[9], 18);
edg_[22] = new concepts::Edge(*vtx_[2], *vtx_[10], 19);
edg_[23] = new concepts::Edge(*vtx_[3], *vtx_[11], 20);
edg_[24] = new concepts::Edge(*vtx_[4], *vtx_[12], 21);
edg_[25] = new concepts::Edge(*vtx_[5], *vtx_[13], 22);
edg_[26] = new concepts::Edge(*vtx_[6], *vtx_[14], 23);
edg_[27] = new concepts::Edge(*vtx_[7], *vtx_[15], 24);
// quadrilaterals on the ground surface
quad_[0] = new concepts::Quad(*edg_[0], *edg_[1], *edg_[2], *edg_[3]);
DEBUGL(1, "0");
quad_[1] = new concepts::Quad(*edg_[3], *edg_[4], *edg_[5], *edg_[6]);
DEBUGL(1, "1");
quad_[2] = new concepts::Quad(*edg_[6], *edg_[7], *edg_[8], *edg_[9]);
DEBUGL(1, "2");
// quadrilaterals on the top surface
quad_[3] = new concepts::Quad(*edg_[10], *edg_[11], *edg_[12], *edg_[13]);
DEBUGL(1, "3");
quad_[4] = new concepts::Quad(*edg_[13], *edg_[14], *edg_[15], *edg_[16]);
DEBUGL(1, "4");
quad_[5] = new concepts::Quad(*edg_[16], *edg_[17], *edg_[18], *edg_[19]);
DEBUGL(1, "5");
// quadrilaterals on the side surfaces
quad_[6] = new concepts::Quad(*edg_[0], *edg_[21], *edg_[10], *edg_[20]);
DEBUGL(1, "6");
quad_[7] = new concepts::Quad(*edg_[1], *edg_[22], *edg_[11], *edg_[21]);
DEBUGL(1, "7");
quad_[8] = new concepts::Quad(*edg_[2], *edg_[23], *edg_[12], *edg_[22]);
DEBUGL(1, "8");
quad_[9] = new concepts::Quad(*edg_[4], *edg_[24], *edg_[14], *edg_[23]);
DEBUGL(1, "9");
quad_[10] = new concepts::Quad(*edg_[5], *edg_[25], *edg_[15], *edg_[24]);
DEBUGL(1, "10");
quad_[11] = new concepts::Quad(*edg_[7], *edg_[26], *edg_[17], *edg_[25]);
DEBUGL(1, "11");
quad_[12] = new concepts::Quad(*edg_[8], *edg_[27], *edg_[18], *edg_[26]);
DEBUGL(1, "12");
quad_[13] = new concepts::Quad(*edg_[9], *edg_[20], *edg_[19], *edg_[27]);
DEBUGL(1, "13");
// inner quadrilaterals
quad_[14] = new concepts::Quad(*edg_[3], *edg_[23], *edg_[13], *edg_[20]);
DEBUGL(1, "14");
quad_[15] = new concepts::Quad(*edg_[6], *edg_[25], *edg_[16], *edg_[20]);
DEBUGL(1, "15");
hex_[0] = new concepts::Hexahedron(*quad_[0], *quad_[6], *quad_[7],
*quad_[8], *quad_[14], *quad_[3]);
hex_[1] = new concepts::Hexahedron(*quad_[1], *quad_[15], *quad_[14],
*quad_[9], *quad_[10], *quad_[4]);
hex_[2] = new concepts::Hexahedron(*quad_[2], *quad_[12], *quad_[13],
*quad_[15], *quad_[11], *quad_[5]);
cell_[0] = new concepts::Hexahedron3d
(*hex_[0],
concepts::MapHexahedron3d(concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(1.0, 0.0, 0.0),
concepts::Real3d(1.0, 1.0, 0.0),
concepts::Real3d(0.0, 1.0, 0.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(1.0, 0.0, 1.0),
concepts::Real3d(1.0, 1.0, 1.0),
concepts::Real3d(0.0, 1.0, 1.0))
);
cell_[1] = new concepts::Hexahedron3d
(*hex_[1],
concepts::MapHexahedron3d(concepts::Real3d(-1.0, 0.0, 0.0),
concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(0.0, 1.0, 0.0),
concepts::Real3d(-1.0, 1.0, 0.0),
concepts::Real3d(-1.0, 0.0, 1.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(0.0, 1.0, 1.0),
concepts::Real3d(-1.0, 1.0, 1.0))
);
cell_[2] = new concepts::Hexahedron3d
(*hex_[2],
concepts::MapHexahedron3d(concepts::Real3d(-1.0, -1.0, 0.0),
concepts::Real3d(0.0, -1.0, 0.0),
concepts::Real3d(0.0, 0.0, 0.0),
concepts::Real3d(-1.0, 0.0, 0.0),
concepts::Real3d(-1.0, -1.0, 1.0),
concepts::Real3d(0.0, -1.0, 1.0),
concepts::Real3d(0.0, 0.0, 1.0),
concepts::Real3d(-1.0, 0.0, 1.0))
);
}
LshapedCube::~LshapedCube() {
for (int i = 0; i < 3; ++i)
delete cell_[i];
for (int i = 0; i < 3; ++i)
delete hex_[i];
for (int i = 0; i < 16; ++i)
delete quad_[i];
for (int i = 0; i < 28; ++i)
delete edg_[i];
for (int i = 0; i < 16; ++i)
delete vtx_[i];
}
std::ostream& LshapedCube::info(std::ostream& os) const {
os << "LshapedCube(" << *cell_[0] << ", " << *cell_[1] << ", "
<< *cell_[2] << ')';
return os;
}
concepts::Quad2d
A 2D cell: quadrilateral.
Definition: cell2D.hh:378
concepts::Scan::eos
virtual bool eos() const =0
Returns true if the end of the scanned set is reached.
concepts::Mesh::info
virtual std::ostream & info(std::ostream &os) const
Returns information in an output stream.
concepts::Scan< Cell3 >
A scanner for a 3D mesh.
Definition: mesh.hh:52
concepts::Quad
A quadrilateral in the topology.
Definition: topology.hh:272
concepts::Mesh3
An abstract class for 3D meshes.
Definition: mesh.hh:112
concepts::Hexahedron3d
A 3D cell: hexahedron.
Definition: cell3D.hh:317
concepts::Scan< Cell2 >
A scanner for a 2D mesh.
Definition: mesh.hh:44
concepts::Cell3
Three dimensional cell.
Definition: cell.hh:112
concepts::Edge1d
A 1D cell: edge.
Definition: cell1D.hh:83
concepts::Triangle2d
A 2D cell: triangle.
Definition: cell2D.hh:31
concepts::Scan::operator++
virtual T & operator++(int)=0
Returns the next element in the scanned set.
concepts::Mesh1::scan
virtual Scan1 * scan()=0
Returns a scanner over the cells of the mesh.
DEBUGL
#define DEBUGL(doit, msg)
concepts::Mesh1
An abstract class for 1D meshes.
Definition: mesh.hh:94
concepts::Cell1
One dimensional cell.
Definition: cell.hh:75
concepts::MapHexahedron3d
A 3D element map for a hexahedron.
Definition: elementMaps3D.hh:366
concepts::Hexahedron
A hexahedron in the topology.
Definition: topology3D.hh:134
concepts::Mesh::ncell
virtual uint ncell() const =0
Returns the number of cells in the mesh.
concepts::Vertex
A vertex in the topology.
Definition: topology.hh:40
concepts::MapQuad2d
A 2D element map for a quadrilateral given by a formula.
Definition: elementMaps.hh:756
concepts::MapEdge1d
A 1D element map for an edge.
Definition: elementMaps.hh:47
concepts::Scan::clone
virtual Scan * clone() const =0
Returns a clone of the scanner.
concepts::Scan
An abstract class for scanning a mesh (a set of cells) or a space (a set of elements).
Definition: scannerConnectors.hh:29
concepts::Mesh2
An abstract class for 2D meshes.
Definition: mesh.hh:103
concepts::Mesh3::scan
virtual Scan3 * scan()=0
Returns a scanner over the cells of the mesh.
concepts::Cell2
Two dimensional cell.
Definition: cell.hh:89
concepts::Mesh2::scan
virtual Scan2 * scan()=0
Returns a scanner over the cells of the mesh.
concepts::VertexTriangle2d
A 2D element map for a triangle.
Definition: elementMaps.hh:557
concepts::Scan< Cell1 >
A scanner for a 1D mesh.
Definition: mesh.hh:36
concepts::Edge
An edge in the topology.
Definition: topology.hh:73
concepts::Triangle
A triangle in the topology.
Definition: topology.hh:193
concepts::Real
double Real
Type normally used for a floating point number.
Definition: typedefs.hh:36
Page URL: http://wiki.math.ethz.ch/bin/view/Concepts/WebHome
21 August 2020
© 2020 Eidgenössische Technische Hochschule Zürich