concepts::MapQuad2d Class Reference
A 2D element map for a quadrilateral given by a formula. More...
#include <elementMaps.hh>
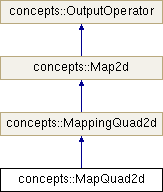
Public Member Functions | |
| virtual MapQuad2d * | clone () const |
| Returns a copy of the map. More... | |
| virtual MappingEdge2d * | edge (const uint edge) const |
| Returns a copy of the edge mapping of one edge. More... | |
| virtual MapReal2d | hessian (uint i, const Real x, const Real y) const |
| Returns the Hessian in a 2D linear map. More... | |
| virtual MapReal2d | inverseLaplace (const Real x, const Real y) const |
| NEW: More... | |
| virtual MapReal2d | jacobian (const Real x, const Real y) const |
| Returns the Jacobian in a 2D linear map. More... | |
| virtual Real | jacobianDeterminant (const Real x, const Real y) const |
| Returns determinant of the Jacobian. More... | |
| virtual MapReal2d | jacobianInverse (const Real x, const Real y) const |
| Returns the inverse of the Jacobian in a 2D linear map. More... | |
| virtual Real | lineElement (const Real x, const uint edge) const |
| Returns factor of differential element integrating over an edge. More... | |
| MapQuad2d (const char *map, Real scX, Real scY, Real2d org, Real2d scaling) | |
| MapQuad2d (const char *map, Real scX, Real scY, Real2d org=Real2d(0.0, 0.0), Real stretch=1.0) | |
| Constructor. More... | |
| MapQuad2d (const MapQuad2d &map) | |
| Copy constructor. More... | |
| virtual Real2d | operator() (Real x, Real y) const |
| Returns a point in 2D mapped from the unit square [0,1]2 onto the element in the original mesh. More... | |
| virtual MappingQuad2d * | part (const Real2d x0, const Real2d y0) const |
| Returns a new object of an element map for a rectangular part of the reference cell defined by the two points. More... | |
| virtual bool | straight () const |
| virtual | ~MapQuad2d () |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. More... | |
Private Member Functions | |
| void | operator= (const MapQuad2d &) |
| Private assignement operator. More... | |
Private Attributes | |
| uchar * | map_ |
| Parsed formula for the map. More... | |
| Real2d | org_ |
| Real2d | scaling_ |
| Real | scx_ |
| Right border of the x parameter domain. More... | |
| Real | scy_ |
| Right border of the y parameter domain. More... | |
| uint | sz_ |
| Length of the parsed formula. More... | |
Detailed Description
A 2D element map for a quadrilateral given by a formula.
The reference element is the unit square. For easier construction of the element map, a rectangle square ![]() can be given as the parameter domain.
can be given as the parameter domain.
If the map gives curved boundaries, they are approxmated better with more refined elements.
- Examples
- meshes.cc.
Definition at line 756 of file elementMaps.hh.
Constructor & Destructor Documentation
◆ MapQuad2d() [1/3]
| concepts::MapQuad2d::MapQuad2d | ( | const char * | map, |
| Real | scX, | ||
| Real | scY, | ||
| Real2d | org = Real2d(0.0, 0.0), |
||
| Real | stretch = 1.0 |
||
| ) |
Constructor.
The values of scX and scY are only for the map, they are not needed by the user for mapping a point from the reference element onto the Real element.
- Parameters
-
map The element map for this quadrilateral as a string, x and y are the variables, the first and the second component are separated by a comma. scX The range of x is [0, scX] scY The range of y is [0, scY] org The origin of the element stretch Scaling factor of the element
◆ MapQuad2d() [2/3]
◆ MapQuad2d() [3/3]
| concepts::MapQuad2d::MapQuad2d | ( | const MapQuad2d & | map | ) |
Copy constructor.
◆ ~MapQuad2d()
|
virtual |
Member Function Documentation
◆ clone()
|
inlinevirtual |
Returns a copy of the map.
Implements concepts::MappingQuad2d.
Definition at line 788 of file elementMaps.hh.
◆ edge()
|
inlinevirtualinherited |
Returns a copy of the edge mapping of one edge.
The edge mappings are directed counter-clockwise, i.e. for the lower edge from the left lower vertex to the right lower one.
- Parameters
-
edge number of edge, i.e. 0 - lower, 1 - right, 2 - upper, 3 - left
Reimplemented in concepts::PartMappingQuad2d, concepts::BlendingQuad2d, and concepts::VertexQuad2d.
Definition at line 731 of file elementMaps.hh.
◆ hessian()
Returns the Hessian in a 2D linear map.
- Parameters
-
i coordinate (0 = x, 1 = y)
Implements concepts::MappingQuad2d.
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Reimplemented from concepts::MappingQuad2d.
◆ inverseLaplace()
◆ jacobian()
Returns the Jacobian in a 2D linear map.
Implements concepts::MappingQuad2d.
◆ jacobianDeterminant()
|
virtualinherited |
Returns determinant of the Jacobian.
◆ jacobianInverse()
|
virtualinherited |
Returns the inverse of the Jacobian in a 2D linear map.
◆ lineElement()
|
virtualinherited |
Returns factor of differential element integrating over an edge.
The factor is either ![]() or
or ![]() .
.
The routine exists explicitly because it is more efficient to implement it than to use jacobian itself, i.e. for affine elements the line element is constant.
- Parameters
-
x local variable on edge (in [0,1]), stands for 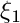 or
or 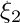
edge number of edge, i.e. 0: 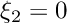 , 1:
, 1: 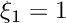 , 2:
, 2: 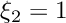 , 3:
, 3: 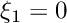
Reimplemented in concepts::BlendingQuad2d, and concepts::VertexQuad2d.
◆ operator()()
Returns a point in 2D mapped from the unit square [0,1]2 onto the element in the original mesh.
- Returns
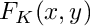
Implements concepts::MappingQuad2d.
Definition at line 779 of file elementMaps.hh.
◆ operator=()
|
private |
Private assignement operator.
◆ part()
|
virtualinherited |
Returns a new object of an element map for a rectangular part of the reference cell defined by the two points.
Reimplemented in concepts::VertexQuad2d.
◆ straight()
|
inlinevirtualinherited |
Reimplemented in concepts::VertexQuad2d, and concepts::VertexTriangle2d.
Definition at line 37 of file elementMaps.hh.
Member Data Documentation
◆ map_
|
private |
Parsed formula for the map.
Definition at line 793 of file elementMaps.hh.
◆ org_
|
private |
Definition at line 804 of file elementMaps.hh.
◆ scaling_
|
private |
Definition at line 805 of file elementMaps.hh.
◆ scx_
|
private |
Right border of the x parameter domain.
Definition at line 799 of file elementMaps.hh.
◆ scy_
|
private |
Right border of the y parameter domain.
Definition at line 802 of file elementMaps.hh.
◆ sz_
|
private |
Length of the parsed formula.
Definition at line 796 of file elementMaps.hh.
The documentation for this class was generated from the following file:
- geometry/elementMaps.hh

