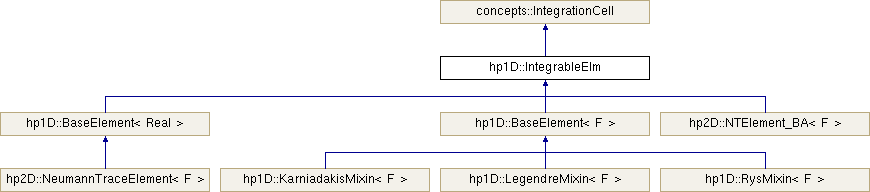
hp1D::IntegrableElm Class Reference
Class holding the quadrature rule and the cell of a 1D element. More...
#include <element.hh>
Public Types | |
| enum | intFormType { ZERO, ONE, TWO, THREE } |
| Integration form, which determines terms coming from integration over reference element. More... | |
Public Member Functions | |
| const concepts::Real3d | chi (const Real x) const |
| Computes the element map. More... | |
| IntegrableElm (const concepts::EdgeNd &cell) | |
| const concepts::QuadratureRule1d * | integration () const |
| Returns the integration rule. More... | |
| Real | jacobianDeterminant (const Real x) const |
| Computes the determinant of the Jacobian. More... | |
| virtual bool | quadraturePoint (uint i, intPoint &p, intFormType form=ZERO, bool localCoord=false) const |
| Delivers a quadrature point. More... | |
Static Public Member Functions | |
| static concepts::QuadRuleFactory & | rule () |
| Access to the quadrature rule, which is valid for all elements of this type (hp1D::IntegrableElm). More... | |
Protected Attributes | |
| const concepts::EdgeNd & | cell_ |
| The cell. More... | |
| std::unique_ptr< concepts::QuadratureRule1d > | int_ |
| The integration rule. More... | |
Static Protected Attributes | |
| static concepts::QuadRuleFactory | rule_ |
Detailed Description
Class holding the quadrature rule and the cell of a 1D element.
Definition at line 34 of file element.hh.
Member Enumeration Documentation
◆ intFormType
|
inherited |
Integration form, which determines terms coming from integration over reference element.
| Enumerator | |
|---|---|
| ZERO | |
| ONE | |
| TWO | |
| THREE | |
Definition at line 29 of file integral.hh.
Constructor & Destructor Documentation
◆ IntegrableElm()
| hp1D::IntegrableElm::IntegrableElm | ( | const concepts::EdgeNd & | cell | ) |
Member Function Documentation
◆ chi()
|
inline |
◆ integration()
|
inline |
Returns the integration rule.
Definition at line 51 of file element.hh.
◆ jacobianDeterminant()
|
inline |
Computes the determinant of the Jacobian.
Definition at line 45 of file element.hh.
◆ quadraturePoint()
|
virtual |
Delivers a quadrature point.
Quadrature point consists of coordinates (for evaluation of formulas) and intermediate data, consisting of the weight and term coming from mapping.
Returns false, if the number of quadrature points is overstepped.
- Parameters
-
i number of quadrature point intPoint data given back form Integration form localCoord If true, local coordinates are returned. Else physical coordinates.
Implements concepts::IntegrationCell.
◆ rule()
|
inlinestatic |
Access to the quadrature rule, which is valid for all elements of this type (hp1D::IntegrableElm).
Change of the quadrature rule is put into practice for newly created elements and for already created elements by precomputing the integration points and shape functions on them.
Definition at line 62 of file element.hh.
Member Data Documentation
◆ cell_
|
protected |
The cell.
Definition at line 70 of file element.hh.
◆ int_
|
protected |
The integration rule.
Definition at line 72 of file element.hh.
◆ rule_
|
staticprotected |
Definition at line 74 of file element.hh.
The documentation for this class was generated from the following file:
- hp1D/element.hh

