hpFEM3d-EV.cc

Introduction

This tutorial is very similar to the two dimensional hp-FEM tutorial in hpFEM2d.cc; you should have read it to understand this tutorial.

Maxwell's Equations

The equations solved are the time-harmonic Maxwell's equations:

\[ - \varepsilon i \omega \vec E + \text{curl} \vec H = \sigma \vec E + \vec J \]

\[ \mu i \omega \vec H + \text{curl} \vec E = 0 \]

with the divergence conditions (assuming no charge density)

\[ \text{div} \mu \vec H = 0 \qquad \text{and} \qquad \text{div} \varepsilon \vec E = 0. \]

Extracting 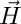$\vec H$ from the second equation and inserting in into the first formally yields

\[ \text{curl}( \mu^{-1} \text{curl} \vec E) - \omega^2 (\varepsilon + \frac{\sigma}{i\omega}) \vec E = -i \omega \vec J, \]

the so-called electric source problem. The appropriate space is

\[ H(\text{curl}; D) := \{\vec u \in L^2(D)^3 : \text{curl} \vec u \in L^2(D)^3 \}. \]

However, the curl-curl form above is not defined for electric fields in 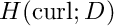$H(\text{curl}; D)$. This is resolved in the variational formulation of the electric source problem:
Find 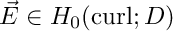$\vec E \in H_0(\text{curl}; D)$ such that

\[ \int_D (\mu^{-1} \text{curl} \vec E \cdot \text{curl} \vec v - \omega^2 \tilde\varepsilon \vec E \cdot \vec v) \, d\vec x = \int_D \vec f \cdot \vec v \, d\vec x \quad \forall \vec v \in H_0(\text{curl}; D), \]

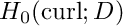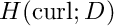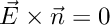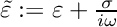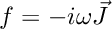where $H_0(\text{curl}; D)$ is $H(\text{curl}; D)$ with the prefect conductor boundary conditions $\vec E \times \vec n = 0$, $\tilde \varepsilon := \varepsilon + \frac{\sigma}{i\omega}$ and $f = -i\omega \vec J$. The associated bilinear operator of this variational formulation is not elliptic and the divergence condition is an independent constraint. Normally, Maxwell's equations are discretised using Nedelec's elements. However, there are good reasons why one would like to use standard H1-conforming FEM. This is possible using weighted regularization.

Weighted Regularization

The divergence can be forced to zero by adding

\[ \int_D \text{div} \vec E \text{div} \vec v \, d\vec x \]

to the bilinear form. However, this works only in non-convex domains. With the weighted regularization and the new bilinear form

\[ \int_D (\mu^{-1} \text{curl} \vec E \cdot \text{curl} \vec v - \omega^2 \tilde\varepsilon \vec E \cdot \vec v) \, d\vec x + \langle\text{div}\vec E, \text{div}\vec v\rangle_Y \]

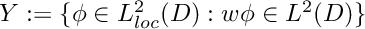where $Y := \{\phi \in L^2_{loc}(D): w\phi \in L^2(D)\}$ and

\[ X_n[Y] := \{\vec u \in H_0(\text{curl}; D): \text{div}\vec u \in Y\} \]

is dense in 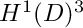$H^1(D)^3$ (the space we are discretising with H1-conforming FEM). A simple choice for the weight $w$ in three dimensions is

\[ w(\vec x) = \text{dist}\left( \vec x, \bigcup_{c \in C} c \cup \bigcup_{e \in E} \bar e \right), \]

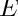where $C$ is the set of reentrant corners and $E$ the set of reentrant edges. Then,

\[ \langle\text{div} \vec u, \text{div} \vec v\rangle_Y = \int_D w^2 \text{div} \vec u \text{div} \vec v \, d\vec x. \]

See also
Martin Costabel and Monique Dauge. Weighted regularization of Maxwell equations in polyhedral domains. A rehabilitation of nodal finite elements. Numer. Math., 93(2):239-277, 2002.

Maxwell Eigenproblem

The Maxwell Eigenproblem is solved using the weighted regularization:
Find frequencies 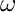$\omega$ and functions $0 \neq \vec E \in X_n[Y]$ such that

\[ \int_D \mu^{-1} \text{curl}\vec E \cdot \text{curl} \vec v\, d\vec x + s\langle\text{div} \vec E, \text{div} \vec v\rangle_Y = \omega^2 \int_D \varepsilon \vec E \cdot \vec v \, d\vec x \quad \forall \vec v \in X_n[Y]. \]

The necessary FE spaces are built using vectorial::Space and hp3D::Space. The bilinear forms are built with hp3D::RotRot, hp3D::DivDiv and vectorial::BilinearForm and hp3D::Identity.

Contents

  1. Commented Program
    1. FEM Routine
    2. Main Program
  2. Results
  3. Complete Source Code

Commented Program

As said above, this tutorial is very similar in large parts to hpFEM2d.cc and the documentation below is terser (ie. only new stuff is commented).

#include <cmath>
#include <cstdlib>
#include <iostream>
#include <sstream>
#include <memory>
#include <fstream>
#include <unistd.h>
#include "basics.hh"
#include "function.hh"
#include "geometry.hh"
#include "graphics.hh"
#include "integration.hh"
#include "operator.hh"
#include "space.hh"
#include "toolbox.hh"

The new includes files are hp3D.hh for the three dimensional hp-FEM, vectorial.hh for the classes to build vector valued FE spaces etc. from the scalar components and eigensolver.hh for the Eigensolvers needed below.

#include "hp3D.hh"
#include "vectorial.hh"
#include "eigensolver.hh"

FEM Routine

Most abbreviations are the same (including the same meaning) as already known.

void fem(const concepts::InOutParameters& input,
concepts::InOutParameters& output) {
const uint l = input.getInt("level");
const uint p = input.getInt("polynomial");
const std::string meshNameBase = input.getString("meshNameBase");

New parameters to configure the Eigensolvers are kmax (how many Eigenvalues should be computed at the same time), solverType (which type of Eigensolver, there are a few available) and shift (parameter 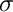$\sigma$ for the shift-invert method).

const uint kmax = input.getInt("kmax");
const Real shift = input.getDouble("shift");

The following parameters are used for the weighted regularization: rho is to distinguish physical from spurious Eigenvalues by the following criterion (using the Eigenfunction 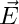$\vec E$):

\[ \frac{\|\text{curl} \vec E\|^2_0}{s \|\text{div} \vec E\|_Y^2} \begin{cases} \geq \rho & \text{physical Eigenvalue} \\ \leq \rho^{-1} & \text{spurious Eigenvalue} \\ \text{otherwise} & \text{undecided}. \end{cases} \]

A good value for rho is 1.5 (the default).

const Real rho = input.getDouble("rho");

weight is used to choose one of various weights (including different weigth exponents (instead of 2 as in the introduction).

const uint weight = input.getInt("weight");

Then, the array for the values of the scaling parameter s are set up.

const uint sNumber = input.getInt("sNumber");
concepts::Array<Real> s(sNumber);
for (uint i = 0; i < sNumber; ++i) s[i] = input.getArrayDouble("s", i);

Mesh

std::stringstream fileCoord;
fileCoord << meshNameBase << "Coord.dat" << std::ends;
output.addString("coordFile", fileCoord.str().c_str());
std::stringstream fileElements;
fileElements << meshNameBase << "Elements.dat" << std::ends;
output.addString("elementsFile", fileElements.str().c_str());
std::stringstream fileBoundary;
fileBoundary << meshNameBase << "Boundary.dat" << std::ends;
output.addString("boundaryFile", fileBoundary.str().c_str());
concepts::Import3dMesh msh(fileCoord.str(), fileElements.str(),
fileBoundary.str());
std::cout << "Mesh: " << msh << std::endl;
graphics::MeshDX<Real>(msh, "mesh.dx");

Space

The perfect conductor boundary conditions 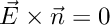$\vec E \times \vec n = 0$ can be set up by carefully choosing the Dirichlet boundary conditions of the three scalar components of the vector valued FE space.

concepts::BoundaryConditions bcX, bcY, bcZ;
bcX.add(concepts::Attribute(1),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(1),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(2),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(2),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(3),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(3),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(4),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(4),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(5),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(5),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(6),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(6),
concepts::Boundary(concepts::Boundary::DIRICHLET));

Finally, the FE spaces can be set up. First, a vector valued FE space with three components is created. This is essentially a container (as most of the classes of vectorial) which takes care of different scalar components which can be added to it.

const uint vdim = 3;
vectorial::Space<Real> spc(vdim);

Then, one after the other scalar FE space is created and added to the vector valued FE space spc. Note that the scalar FE spaces have to be rebuilt before adding them to spc. This call to hp3D::Space::rebuild creates the elements.

hp3D::Space sspcX(msh, 0, p, &bcX); sspcX.rebuild(); spc.put(sspcX);
hp3D::Space sspcY(msh, 0, p, &bcY); sspcY.rebuild(); spc.put(sspcY);
hp3D::Space sspcZ(msh, 0, p, &bcZ); sspcZ.rebuild(); spc.put(sspcZ);
for (uint i = 0; i < l; ++i) {
std::cout << "i = " << i << std::endl;
concepts::ResourceMonitor timer;

The scalar spaces also have to be rebuilt separately after a refinement before rebuilding the vector valued space.

sspcX.rebuild();
std::cout << " scalar space: " << std::flush;
std::cout << sspcX << std::endl;
output.addArrayInt("dof", i, spc.dim());
output.addArrayDouble("space_time", i, timer.utime());
// graphics of the mesh
graphics::MeshDX<Real>(sspcX, "space.dx", 3);
graphics::drawMeshTecplot(sspcX, "space.dat", 3);
if (spc.dim() > 20) {

Computations

The stiffness matrix has two parts: rot-rot and div-div. These two parts are built separately. Before calling the Eigensolver, a linear combination depending on s of the two is created. The classes hp3D::RotRot and hp3D::DivDiv both come with a setup routine to take care of some technicalities. The use of this routine is not mandatory but recommended.

The rot-rot part of the stiffness matrix is simple to compute.

// ** stiffness matrix **
vectorial::BilinearForm<Real> vrotrot_bf(vdim);
hp3D::RotRot::setup(vrotrot_bf);
concepts::SparseMatrix<Real> rotrot(spc, vrotrot_bf);
rotrot.compress();
std::cout << " rot rot matrix: " << rotrot << std::endl;

The div-div part of the stiffness matrix is somewhat more involved: the singularities of the solutions have to be taken into account by the weight. The singular edes and vertices are marked, this information is later used by the div-div bilinear form.

hp3D::SingularSet singularities;
singularities.add(concepts::Attribute(input.getInt("vtxRef")), msh);
singularities.add(concepts::Attribute(input.getInt("edgRef")), msh);

Various weights can be selected on the command line or via the input file. This is reflected in weight.

vectorial::BilinearForm<Real> vdivdiv_bf(vdim);
switch (weight) {
case 0: // TrivialWeight
hp3D::DivDiv<hp3D::TrivialWeight>::setup(vdivdiv_bf, singularities);
break;
case 1: // ShortestDist
hp3D::DivDiv<hp3D::ShortestDist>::setup(vdivdiv_bf, singularities);
break;
case 11: // ProductOfAll
hp3D::DivDiv<hp3D::ProductOfAll>::setup(vdivdiv_bf, singularities);
break;
case 21: // DaugeWeight
hp3D::DivDiv<hp3D::DaugeWeight>::setup(vdivdiv_bf, singularities);
break;
default: throw conceptsException(concepts::ExceptionBase());
}
std::cout << " div div bilinear form: "
<< *(vdivdiv_bf.get(0)) << std::endl;
std::stringstream weightName;
weightName << *(vdivdiv_bf.get(0));
output.addString("weight", weightName.str().c_str());

After having selected the right bilinear form (the right weight for the div-div form), the div-div stiffness matrix can be computed

concepts::SparseMatrix<Real> divdiv(spc, vdivdiv_bf);
divdiv.compress();
std::cout << " div div matrix: " << divdiv << std::endl;

The mass matrix consists of three scalar mass matrices in the diagonal blocks of the mass matrix. They are put together in the canonical way to build a vector valued bilnear form.

// ** mass matrix **
hp3D::Identity<> smass_bf;
vectorial::BilinearForm<Real> mass_bf(vdim);

Each call to vectorial::BilinearForm::put adds a scalar bilinear form into a block of the vector valued bilinear form. In this case, only the diagonal blocks have to be filled.

mass_bf.put(smass_bf, 0, 0);
mass_bf.put(smass_bf, 1, 1);
mass_bf.put(smass_bf, 2, 2);
concepts::SparseMatrix<Real> mass(spc, mass_bf);
std::cout << " mass matrix: " << mass << std::endl;
output.addArrayDouble("matrix_time", i, timer.utime());
mass.compress();
std::cout << " mass matrix: " << mass << std::endl;

The next step is to set up the solver. There is loop over the different values of the scaling parameter s around the solution process.

// ** solver **
for (uint sIndex = 0; sIndex < sNumber; ++sIndex) {
std::cout << " s = " << s[sIndex] << std::endl;
concepts::SparseMatrix<Real> stiff(rotrot);

The Eigensolver shall be constructed by a fabric, ie. a class derived from eigensolver::SolverFabric. solverType contains which solver to use and it is evaluated in the following switch case clause.

After having chosen the solver by creating the appropriate fabric, the solver can be instantiated.

A call to eigensolver::Solver::getEV returns the Eigenvalues. They are printed to screen in a list.

Postprocessing

Then, a list of the Eigenvalues together with the categorization (the formula is given above) is printed to screen. In addition, the Eigenvalue together with the rotrot energy and the divdiv energy are stored in the output data for later postprocessing (or plotting).

Compute the rotrot energy: 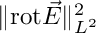$\|\text{rot} \vec E\|^2_{L^2}$

Compute the divdiv energy: 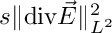$s\|\text{div} \vec E\|^2_{L^2}$

Evaluate the criterion and print the results.

Finally, the data is stored in output.

Refinement of the Space

Each component of the vector valued space has to be refined individually towards the singularly marked vertices and edges.

Main Program

The main program works very similar to the previous tutorials.

Command Line Arguments

The arrays to store the Eigenvalues and the divdiv and rotrot energies have to be prepared.

Results

To restrict the amount of output, we are calling the program with the following input file:@code int level 1 int kmax 3 int sNumber 1 array double s { 0 2.0 } Then, the output looks like:

[./hpFEM3d-EV]
--
Parameters:
input file = t.concepts
string author "(empty)"
string comment "(empty)"
string gnuplot "./hpFEM3d-EV.gnuplot"
string meshNameBase "../../../applications/thickLshape"
string parameterout "./hpFEM3d-EV.out"
string title "Maxwell Eigenvalues in 3D using weighted regularization"
int edgRef 77
int faceRef 0
int kmax 3
int level 1
int polynomial 2
int sNumber 1
int solver 2
int vtxRef 66
int weight 11
double rho 1.5
double shift 9
array double s {
0 2
1 2
2 3
3 4
4 20
5 9
6 12
7 15
8 17
9 30
}
--
Mesh: Import3dMesh(ncell = 3)
i = 0
scalar space: Space(dim = 7, nelm = 3)
Space(dim = 7, nelm = 3)
Space(dim = 12, nelm = 3)
vector valued space (3 comp.): Space(idx = 3, vdim = 3, dim = 26, nelm = 3)
rot rot matrix: SparseMatrix(26x26, HashedSparseMatrix: 316 (46.7456%) entries bound.)
div div bilinear form: DivDiv(weight = ProductOfAll)
div div matrix: SparseMatrix(26x26, HashedSparseMatrix: 334 (49.4083%) entries bound.)
mass matrix: SparseMatrix(26x26, HashedSparseMatrix: 426 (63.0178%) entries bound.)
mass matrix: SparseMatrix(26x26, HashedSparseMatrix: 158 (23.3728%) entries bound.)
s = 2
solver = ArPack(shift-invert mode(3), not yet computed largest (algebraic) eigenvalues, sigma = 9, n = 26, tol = 0, conv. eigenpairs = 0(max = 3), Arnoldi iter = 0(max = 1000), 0 OP*x ops., 0 B*x ops., 0 steps of re-orth.)
Eigenvalues: Array<F>(3, [9.90411138346484, 14.167902552732, 14.5499375050742])
solver = ArPack(shift-invert mode(3), computed largest (algebraic) eigenvalues, sigma = 9, n = 26, tol = 1.11022302462516e-16, conv. eigenpairs = 3(max = 3), Arnoldi iter = 13(max = 1000), 34 OP*x ops., 112 B*x ops., 33 steps of re-orth.)
EV 0 = 9.90411138346484 has rotEnergy = 9.9041, divEnergy*s = 7.1322e-32, L2 norm = 1
EV 1 = 14.167902552732 has rotEnergy = 13.806, divEnergy*s = 0.36222, L2 norm = 1
EV 2 = 14.5499375050742 has rotEnergy = 13.526, divEnergy*s = 1.0238, L2 norm = 1
--
Writing gathered data to disk: ./hpFEM3d-EV.out

The mesh normally used is a thick L shaped domain in three hexahedra. The mesh looks like this: 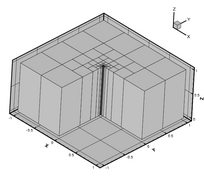Mesh in thick L shaped domain With 18726 dofs, the Eigenvalues plotted versus s: 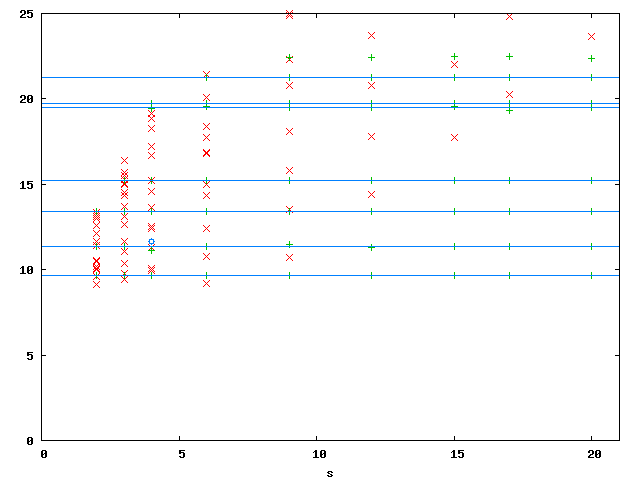Eigenvalues-s plot The physical Eigenvalues (green) are lined up on horizontal lines whereas the spurious Eigenvalues are on straight lines through the origin. The exact values (horizontal blue lines) are taken from Monique Dauge's Benchmax page. 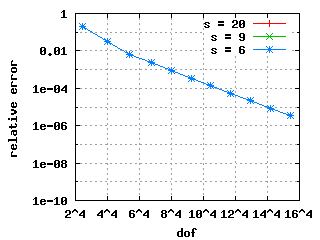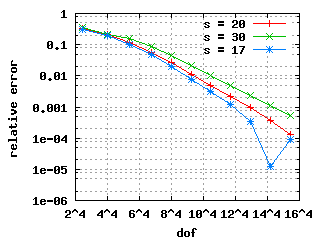Below are the convergence histories for the first three Eigenvalues for selected values of s: 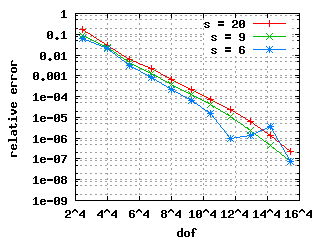Convergence history of 1st Eigenvalue Convergence history of 2nd Eigenvalue Convergence history of 3rd Eigenvalue These convergence histories show exponential convergence: straight lines in a $ \log-\sqrt[4]{.} $ plot.

Complete Source Code

Author
Philipp Frauenfelder, 2004
#include <cmath>
#include <cstdlib>
#include <iostream>
#include <sstream>
#include <memory>
#include <fstream>
#include <unistd.h>
#include "basics.hh"
#include "function.hh"
#include "geometry.hh"
#include "graphics.hh"
#include "integration.hh"
#include "operator.hh"
#include "space.hh"
#include "toolbox.hh"
#include "hp3D.hh"
#include "vectorial.hh"
#include "eigensolver.hh"
// ************************************************************* fem routine **
void fem(const concepts::InOutParameters& input,
concepts::InOutParameters& output) {
const uint l = input.getInt("level");
const uint p = input.getInt("polynomial");
const std::string meshNameBase = input.getString("meshNameBase");
const uint kmax = input.getInt("kmax");
const Real shift = input.getDouble("shift");
const Real rho = input.getDouble("rho");
const uint weight = input.getInt("weight");
const uint sNumber = input.getInt("sNumber");
concepts::Array<Real> s(sNumber);
for (uint i = 0; i < sNumber; ++i) s[i] = input.getArrayDouble("s", i);
// mesh import: generate names
std::stringstream fileCoord;
fileCoord << meshNameBase << "Coord.dat" << std::ends;
output.addString("coordFile", fileCoord.str().c_str());
std::stringstream fileElements;
fileElements << meshNameBase << "Elements.dat" << std::ends;
output.addString("elementsFile", fileElements.str().c_str());
std::stringstream fileBoundary;
fileBoundary << meshNameBase << "Boundary.dat" << std::ends;
output.addString("boundaryFile", fileBoundary.str().c_str());
concepts::Import3dMesh msh(fileCoord.str(), fileElements.str(),
fileBoundary.str());
std::cout << "Mesh: " << msh << std::endl;
graphics::MeshDX<Real>(msh, "mesh.dx");
concepts::BoundaryConditions bcX, bcY, bcZ;
bcX.add(concepts::Attribute(1),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(1),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(2),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(2),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(3),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(3),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(4),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(4),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcZ.add(concepts::Attribute(5),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(5),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcX.add(concepts::Attribute(6),
concepts::Boundary(concepts::Boundary::DIRICHLET));
bcY.add(concepts::Attribute(6),
concepts::Boundary(concepts::Boundary::DIRICHLET));
const uint vdim = 3;
vectorial::Space<Real> spc(vdim);
hp3D::Space sspcX(msh, 0, p, &bcX); sspcX.rebuild(); spc.put(sspcX);
hp3D::Space sspcY(msh, 0, p, &bcY); sspcY.rebuild(); spc.put(sspcY);
hp3D::Space sspcZ(msh, 0, p, &bcZ); sspcZ.rebuild(); spc.put(sspcZ);
for (uint i = 0; i < l; ++i) {
std::cout << "i = " << i << std::endl;
concepts::ResourceMonitor timer;
sspcX.rebuild();
std::cout << " scalar space: " << std::flush;
std::cout << sspcX << std::endl;
sspcY.rebuild();
std::cout << " " << sspcY << std::endl;
sspcZ.rebuild();
std::cout << " " << sspcZ << std::endl;
spc.rebuild();
std::cout << " vector valued space (" << vdim << " comp.): "
<< std::flush;
std::cout << spc << std::endl;
output.addArrayInt("dof", i, spc.dim());
output.addArrayDouble("space_time", i, timer.utime());
// graphics of the mesh
graphics::MeshDX<Real>(sspcX, "space.dx", 3);
graphics::drawMeshTecplot(sspcX, "space.dat", 3);
if (spc.dim() > 20) {
// ** stiffness matrix **
vectorial::BilinearForm<Real> vrotrot_bf(vdim);
hp3D::RotRot::setup(vrotrot_bf);
concepts::SparseMatrix<Real> rotrot(spc, vrotrot_bf);
rotrot.compress();
std::cout << " rot rot matrix: " << rotrot << std::endl;
hp3D::SingularSet singularities;
singularities.add(concepts::Attribute(input.getInt("vtxRef")), msh);
singularities.add(concepts::Attribute(input.getInt("edgRef")), msh);
vectorial::BilinearForm<Real> vdivdiv_bf(vdim);
switch (weight) {
case 0: // TrivialWeight
hp3D::DivDiv<hp3D::TrivialWeight>::setup(vdivdiv_bf, singularities);
break;
case 1: // ShortestDist
hp3D::DivDiv<hp3D::ShortestDist>::setup(vdivdiv_bf, singularities);
break;
case 11: // ProductOfAll
hp3D::DivDiv<hp3D::ProductOfAll>::setup(vdivdiv_bf, singularities);
break;
case 21: // DaugeWeight
hp3D::DivDiv<hp3D::DaugeWeight>::setup(vdivdiv_bf, singularities);
break;
default: throw conceptsException(concepts::ExceptionBase());
}
std::cout << " div div bilinear form: "
<< *(vdivdiv_bf.get(0)) << std::endl;
std::stringstream weightName;
weightName << *(vdivdiv_bf.get(0));
output.addString("weight", weightName.str().c_str());
concepts::SparseMatrix<Real> divdiv(spc, vdivdiv_bf);
divdiv.compress();
std::cout << " div div matrix: " << divdiv << std::endl;
// ** mass matrix **
hp3D::Identity<> smass_bf;
vectorial::BilinearForm<Real> mass_bf(vdim);
mass_bf.put(smass_bf, 0, 0);
mass_bf.put(smass_bf, 1, 1);
mass_bf.put(smass_bf, 2, 2);
concepts::SparseMatrix<Real> mass(spc, mass_bf);
std::cout << " mass matrix: " << mass << std::endl;
output.addArrayDouble("matrix_time", i, timer.utime());
mass.compress();
std::cout << " mass matrix: " << mass << std::endl;
// ** solver **
for (uint sIndex = 0; sIndex < sNumber; ++sIndex) {
std::cout << " s = " << s[sIndex] << std::endl;
concepts::SparseMatrix<Real> stiff(rotrot);
divdiv.addInto(stiff, s[sIndex]);
eigensolver::EasyArPackppGen<Real, Real> eigensolver(stiff, mass, kmax, shift);
// ** results **
const concepts::Array<concepts::Cmplx>& sol_eigenvalue = eigensolver.getSolver()->getEV();
const concepts::Array<concepts::Vector<concepts::Cmplx>*>& sol_eigenfunction
= eigensolver.getSolver()->getEF();
if (sIndex == 0)
output.addArrayDouble("solve_time", i, timer.utime());
const uint nEV = sol_eigenvalue.size();
std::cout.precision(15);
std::cout << " Eigenvalues: " << sol_eigenvalue << std::endl;
// computing Rotrot and Divdiv energies
for (uint evIndex = 0; evIndex < nEV; ++evIndex) {
concepts::Vector<concepts::Cmplx> tmp(spc);
rotrot(*(sol_eigenfunction[evIndex]), tmp);
Real rotEnergy = real(*(sol_eigenfunction[evIndex]) * tmp);
divdiv(*(sol_eigenfunction[evIndex]), tmp);
Real divEnergy = real(*(sol_eigenfunction[evIndex]) * tmp) * s[sIndex];
std::string quality;
if ( std::fabs(rotEnergy)/std::fabs(divEnergy) >= rho) {
quality = "**";
} else {
if ( std::fabs(rotEnergy)/std::fabs(divEnergy) <= 1./rho)
quality = " ";
else quality = " *";
}
std::cout << quality << " EV " << evIndex << " = ";
std::cout.precision(15);
std::cout << sol_eigenvalue[evIndex];
std::cout.precision(5);
mass(*(sol_eigenfunction[evIndex]), tmp);
Real L2norm = real(*(sol_eigenfunction[evIndex]) * tmp);
std::cout << " has rotEnergy = " << rotEnergy
<< ", divEnergy*s = " << divEnergy
<< ", L2 norm = " << L2norm
<< std::endl;
std::stringstream name1, name2, name3;
name1 << "ev_s_" << s[sIndex] << "_k_" << evIndex << std::ends;
output.addArrayDouble(name1.str().c_str(), i,
sol_eigenvalue[evIndex].real());
name2 << "dE_s_" << s[sIndex] << "_k_" << evIndex << std::ends;
output.addArrayDouble(name2.str().c_str(), i, divEnergy);
name3 << "rE_s_" << s[sIndex] << "_k_" << evIndex << std::ends;
output.addArrayDouble(name3.str().c_str(), i, rotEnergy);
} // for evIndex
} // for sIndex
} // if dim > 20
// ** refinement **
if (i < l-1) {
int pMax[3] = { 1, 1, 1 };
hp3D::Space* spaces[3] = { &sspcX, &sspcY, &sspcZ };
for (uint j = 0; j < 3; ++j) {
hp3D::APrioriRefinement refineSpace
(*spaces[j], input.getInt("vtxRef"), input.getInt("edgRef"),
input.getInt("faceRef"), pMax);
concepts::GlobalPostprocess<Real> post(*spaces[j]);
post(refineSpace);
} // loop over three components
std::cout << "--" << std::endl;
} // if i < l-1
} // for i
}
// ************************************************************ Main Program **
int main(int argc, char** argv) {
try {
concepts::InputParser inputParser;
concepts::InOutParameters& input = inputParser.inputParameters();
input.addInt("level", 2);
input.addInt("polynomial", 2);
input.addString("meshNameBase", SOURCEDIR "/applications/thickLshape");
input.addInt("vtxRef", 66);
input.addInt("edgRef", 77);
input.addInt("faceRef", 0);
input.addInt("kmax", 20);
input.addInt("solver", 2);
input.addDouble("shift", 9.0);
input.addDouble("rho", 1.5);
input.addInt("weight", 11);
input.addInt("sNumber", 10);
concepts::Array<Real> s(input.getInt("sNumber"));
s[0] = 6;
s[1] = 2;
s[2] = 3;
s[3] = 4;
s[4] = 20;
s[5] = 9;
s[6] = 12;
s[7] = 15;
s[8] = 17;
s[9] = 30;
input.addArrayDouble("s");
for (uint i = 0; i < (uint)input.getInt("sNumber"); ++i)
input.addArrayDouble("s", i, s[i]);
input.addString("title",
"Maxwell Eigenvalues in 3D using weighted regularization");
std::stringstream outfile;
outfile << argv[0] << ".out" << std::ends;
input.addString("parameterout", outfile.str().c_str());
std::stringstream gnuplotfile;
gnuplotfile << argv[0] << ".gnuplot" << std::ends;
input.addString("gnuplot", gnuplotfile.str().c_str());
concepts::InOutParameters& output = inputParser.outputParameters();
output.addString("version", "$Id: hpFEM3d-EV.cc,v 1.5 2005/08/26 15:35:48 kersten Exp $");
output.addArrayInt("dof");
output.addArrayDouble("space_time");
output.addArrayDouble("matrix_time");
output.addArrayDouble("solve_time");
concepts::ResultsTable table;
table.addMap(concepts::ResultsTable::INT, "dof", output);
table.addMap(concepts::ResultsTable::DOUBLE, "space_time", output);
table.addMap(concepts::ResultsTable::DOUBLE, "matrix_time", output);
table.addMap(concepts::ResultsTable::DOUBLE, "solve_time", output);
// ********************************************************** input data **
std::string inputfile;
int opt;
while ((opt = getopt(argc, argv, "-f:e:l:p:k:r:n:s:w:")) != EOF)
switch(opt) {
case 'l': input.addInt("level", atoi(optarg)); break;
case 'p': input.addInt("polynomial", atoi(optarg)); break;
case 'f': inputfile = std::string(optarg);
inputParser.parse(inputfile);
break;
case 'e': input.addInt("solver", std::atoi(optarg)); break;
case 'k': input.addInt("kmax", std::atoi(optarg)); break;
case 'r': input.addDouble("rho", std::atof(optarg)); break;
case 'n': input.addString("meshNameBase", optarg); break;
case 's': input.addDouble("shift", std::atof(optarg)); break;
case 'w': input.addInt("weight", std::atoi(optarg)); break;
default:
std::cout << "Option '" << opt << "' unkown." << std::endl
<< "Usage: " << argv[0]
<< " [-f FILE] [-l LEVEL] [-e SOLVER] [-k KMAX] [-p POLY] "
<< "[-r RHO] [-n MESH_NAME] [-s SHIFT] [-w WEIGHT]"
<< std::endl
<< "where" << std::endl
<< " FILE: name of the input file" << std::endl
<< " LEVEL: level of refinement" << std::endl
<< " SOLVER: JDBSYM(0), ARPACK(1)" << std::endl
<< " POLY: starting polynomial degree" << std::endl
<< " KMAX: number of eigenvalues which should be computed"
<< std::endl
<< " MESH_NAME: name of the mesh (thickLshape)" << std::endl
<< " SHIFT: shift for Eigenvalue solver" << std::endl
<< " WEIGHT:" << std::endl
<< " 0: TrivialWeight" << std::endl
<< " 1: ShortestDist" << std::endl
<< " 11: ProductOfAll" << std::endl
<< " 21: DaugeWeight" << std::endl
<< "Options given after the input file override the values "
<< "read from the"
<< std::endl << "input file." << std::endl;
exit(1);
break;
}
// ********************************** create output area for eigenvalues **
for (uint i = 0; i < (uint)input.getInt("sNumber"); ++i) {
for (uint j = 0; j < (uint)input.getInt("kmax"); ++j) {
std::stringstream name1, name2, name3;
name1 << "ev_s_" << input.getArrayDouble("s", i) << "_k_" << j
<< std::ends;
output.addArrayDouble(name1.str().c_str());
table.addMap(concepts::ResultsTable::DOUBLE, name1.str().c_str(),
output);
name2 << "dE_s_" << input.getArrayDouble("s", i) << "_k_" << j
<< std::ends;
output.addArrayDouble(name2.str().c_str());
table.addMap(concepts::ResultsTable::DOUBLE, name2.str().c_str(),
output);
name3 << "rE_s_" << input.getArrayDouble("s", i) << "_k_" << j
<< std::ends;
output.addArrayDouble(name3.str().c_str());
table.addMap(concepts::ResultsTable::DOUBLE, name3.str().c_str(),
output);
}
}
// ***************************************************** show parameters **
std::cout << '[' << argv[0] << "]" << std::endl;
std::cout << "--" << std::endl;
std::cout << "Parameters:" << std::endl
<< " input file = " << inputfile << std::endl
<< input;
std::cout << "--" << std::endl;
// ******************************************************** computations **
fem(input, output);
// ************************************** output of input data and other **
std::ofstream* ofs = new std::ofstream
(input.getString("gnuplot").c_str());
*ofs << std::setprecision(20);
table.print<concepts::ResultsTable::GNUPLOT>(*ofs);
delete ofs;
std::cout << " --" << std::endl
<< " Writing gathered data to disk: "
<< input.getString("parameterout") << std::endl;
ofs = new std::ofstream(input.getString("parameterout").c_str());
*ofs << "/* program:\t" << argv[0] << std::endl
<< " * command:\t";
for (int j = 0; j < argc; ++j)
*ofs << argv[j] << " ";
*ofs << std::endl
<< " * input file:\t" << inputfile << std::endl;
*ofs << " */" << std::endl << std::setprecision(20) << inputParser;
delete ofs;
}
catch(concepts::ExceptionBase& e) {
std::cout << e << std::endl;
return 1;
}
return 0;
}
concepts::Array::size
uint size() const
Returns the requested size of the array.
Definition: array.hh:259
hp3D::RotRot::setup
static void setup(vectorial::BilinearForm< Real, Real > &bf)
Sets up the bilinear form for the rot-rot part for Maxwell's equation using weighted regularization.
vectorial::Space
Vector valued space.
Definition: spaceTraits.hh:26
conceptsException
#define conceptsException(exc)
Prepares an exception for throwing.
Definition: exceptions.hh:344
concepts::ExceptionBase
Base class for exceptions.
Definition: exceptions.hh:86
vectorial::BilinearForm
Vector valued bilinear form.
Definition: bf_advection.hh:38
concepts::BoundaryConditions::add
void add(const Set< Attribute > &attrib, const Boundary &bcObject)
Adds a boundary condition with this attribute to the list of boundary conditions.
std::norm
const concepts::Real norm(const concepts::Real &v)
Returns the square of a real value.
Definition: operations.hh:90
concepts::InOutParameters
Holds parameters in hashes.
Definition: inputOutput.hh:75
concepts::SparseMatrix::compress
void compress(Real threshold=EPS)
Compresses the matrix by dropping small entries.
Definition: sparseMatrix.hh:444
hp3D::Space
A 3D hp FEM space with continuous, picewise polynomial basis functions.
Definition: space.hh:84
concepts::ResourceMonitor
Timer and resource monitor.
Definition: resourceMonitor.hh:29
concepts::SparseMatrix::addInto
void addInto(Matrix< H > &dest, const I fact, const uint rowoffset=0, const uint coloffset=0) const
This matrix is added as block to the given matrix dest.
Definition: sparseMatrix.hh:538
hp3D::APrioriRefinement
Carries out a-priori given refinements.
Definition: aprioriRef.hh:39
concepts::InOutParameters::addArrayDouble
void addArrayDouble(const char *array, const bool newArray=false)
Creates an empty array for doubles if necessary.
concepts::InOutParameters::getDouble
double getDouble(const char *name) const
Returns a double from the hash of doubles.
hp3D::Space::rebuild
Space rebuild()
Rebuilds the space after an adjustment with adjust.
concepts::InOutParameters::getInt
int getInt(const char *name, const int value=INT_MAX) const
Returns an int from the hash of ints.
concepts::Boundary
Class to describe an element of the boundary.
Definition: boundary.hh:35
concepts::InOutParameters::addArrayInt
void addArrayInt(const char *array, const bool newArray=false)
Creates an empty array for ints if necessary
eigensolver::EasyArPackppGen
Tool to easily solve general eigenvalue problems.
Definition: easyArpackpp.hh:151
concepts::InOutParameters::addString
void addString(const char *name, const char *value)
Adds a string to the hash of strings.
vectorial::BilinearForm::put
virtual void put(concepts::BilinearForm< F, G > &bf, const int i, const int j)
insert a Bilinearform bf of one vectorial dimension to the all v-dimensionial Bilinearform
concepts::InputParser
Parses an input file and extracts parameters.
Definition: inputOutput.hh:443
concepts::ResultsTable::addMap
void addMap(enum mapTypes type, const char *name, const InOutParameters &holder)
concepts::InputParser::inputParameters
InOutParameters & inputParameters()
Returns the input data.
Definition: inputOutput.hh:461
hp3D::DivDiv::setup
static void setup(vectorial::BilinearForm< Real, Real > &bf, hp3D::SingularSet &singularities, const concepts::Formula< Real > *frm=0)
Sets up the bilinear form for the div-div part for Maxwell's equation using weighted regularization.
graphics::drawMeshTecplot
void drawMeshTecplot(concepts::Mesh &msh, const std::string &filename)
Trampoline function to create an instance of MeshTecplot.
concepts::InOutParameters::addInt
void addInt(const char *name, const int value)
Adds an int to the hash of ints.
concepts::InputParser::outputParameters
InOutParameters & outputParameters()
Returns the output data.
Definition: inputOutput.hh:464
concepts::InOutParameters::getArrayDouble
double getArrayDouble(const char *array, const int number) const
Returns a double from an array.
concepts::Import3dMesh
Imports 3D mesh with tetrahedra and hexahedra.
Definition: meshImport3D.hh:94
concepts::InOutParameters::getString
std::string getString(const char *name, const char *value=0) const
Returns a string from the hash of strings.
concepts::InputParser::parse
void parse()
Parses the input file.
concepts::ResultsTable
Organizes the results in the hashes from InOutParameters in a nice table.
Definition: resultsTable.hh:23
hp3D::SingularSet
Class for handling a set of singular edges and vertices.
Definition: singularSet.hh:136
concepts::ResultsTable::print
void print(std::ostream &os) const
hp3D::SingularSet::add
void add(const concepts::Attribute &attrib, concepts::Mesh3 &msh)
Add all vertices and edges in the mesh with attrib to the set of singular vertices and edges.
hp3D::Identity
A function class to calculate element matrices for the mass matrix.
Definition: bilinearForm.hh:84
eigensolver
Eigenvalue solvers.
Definition: ARPACK.hh:19
concepts::InOutParameters::addDouble
void addDouble(const char *name, const double value)
Adds a double to the hash of doubles.
concepts::Attribute
Attributes for elements of the topology.
Definition: connector.hh:22
concepts::Real
double Real
Type normally used for a floating point number.
Definition: typedefs.hh:36
graphics::MeshDX
Draws a picture of a mesh in DX format and stores the result in a file.
Definition: meshDX.hh:89
concepts::ResourceMonitor::utime
float utime()
Returns the user time since the last call of ResourceMonitor using getrusage.
Page URL: http://wiki.math.ethz.ch/bin/view/Concepts/WebHome
21 August 2020
© 2020 Eidgenössische Technische Hochschule Zürich