Preprints
- 3-braid knots with maximal 4-genus, arXiv:2303.11918, with Sebastian Baader, Lukas Lewark, Filip Misev.
- Strongly quasipositive links are concordant to infinitely many strongly quasipositive links, arXiv:2210.06612.
- On the nonorientable four-ball genus of torus knots, arXiv:2109.09187, with Fraser Binns, Sungkyung Kang, Jonathan Simone.
- The upsilon invariant at \(1\) of \(3\)-braid knots, arXiv:2108.03674. Accepted for publication in Algebraic & Geometric Topology.
Recordings of talks
- Strongly quasipositive knots are concordant to infinitely many strongly
quasipositive knots, The Low-dimensional Workshop, Erdős Center, Alfréd
Rényi Institute of Mathematics, Budapest. Here is a recording of my (blackboard) talk.
- Strongly quasipositive knots are concordant to infinitely many strongly
quasipositive knots, Geometry and Topology Seminar, CIRGET (online), December 2022. Here is a recording of my talk and
here are my slides.
My research interests
- Strongly quasipositive knots are concordant to infinitely many strongly quasipositive knots, The Low-dimensional Workshop, Erdős Center, Alfréd Rényi Institute of Mathematics, Budapest. Here is a recording of my (blackboard) talk.
- Strongly quasipositive knots are concordant to infinitely many strongly quasipositive knots, Geometry and Topology Seminar, CIRGET (online), December 2022. Here is a recording of my talk and here are my slides.
My research interests
I am interested in low-dimensional topology, which is the area in topology that studies manifolds of dimension \(4\) and below. In particular, I like to study knots as closures of braids, and I like to think about (non)orientable surfaces embedded in the \(4\)-ball that bound a given knot in the \(3\)-sphere or two such knots, for example knot concordances. In this September 2021 report you can read more about a particular question that interests me.
Below is an informal introduction to the following topics:
What is knot theory?
Slice knots and knot concordance
Knots as closures of braids
What is knot theory?
Classical knots in dimension \(3\) are smooth embeddings of the (oriented) sphere \(S^1\) into Euclidean \(3\)-space \(\mathbb{R}^3\) or (more often) the \(3\)-sphere \(S^3 \cong \mathbb{R}^3 \cup \{\infty \}\). We identify such embeddings with their images and consider two of them to be equivalent and the images to be isotopic knots or knots of the same type if the embeddings are ambient isotopic.
Originally, knot theorists tried to distinguish isotopy classes of knots using tools from algebra, analysis, geometry and topology in order to tabulate them. A knot invariant is a function which assigns to each knot \(K\) an object \(f(K)\) in such a way that knots of the same type are assigned equivalent objects.
An example is the group of a knot \(K\) which is the fundamental group of the complement of \(K\) in \(S^3\). Although it is not a complete knot invariant, i.e. non-isotopic knots could be assigned isomorphic groups, the group of a knot is so far one of the strongest known tools to recognize different knot types. A consequence of Dehn's lemma - a deep result in the study of \(3\)-dimensional manifolds stated by Dehn in the beginning of the 20th century, but only proven by Papakyriakopolous in 1957 - is that there is only one knot type which has an infinite cyclic knot group: the unknot, represented by the embedding \(S^1 \hookrightarrow \mathbb{R}^2 \times \{0\} \subset \mathbb{R}^2 \times \mathbb{R} \cong \mathbb{R}^3 \subset S^3\). This embedding extends to an embedding of a disk \(D^2 \hookrightarrow \mathbb{R}^2 \times \{0\} \subset \mathbb{R}^2 \times \mathbb{R} \subset S^3\) and it turns out that a knot is isotopic to the unknot if and only if it bounds an embedded disk in \(S^3\).
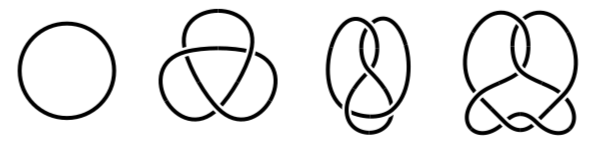
Several different knots: the unknot, the trefoil, the figure eight knot and the easiest (in terms of crossing number) non-trivial prime slice knot \(6_1\)
Slice knots and knot concordance
The concept of "sliceness" is in a sense a natural generalization in dimension \(4\) of the question whether certain knots are isotopic to the unknot.
A knot \(K\) in \(S^3\) is slice if it bounds a smoothly embedded \(2\)-dimensional disk \(D^2\) in \(B^4\), the \(4\)-ball bounded by \(S^3\).
It is one of the mysteries of \(4\)-dimensional topology that constructions such as finding slice disks can sometimes be done in the topological category but fail to work smoothly.
In 1982 Freedman showed that knots with trivial Alexander polynomial are topologically slice, i.e. they bound a locally flat disk in \(B^4\). Gompf used this result to find the first infinite family of knots that are topologically slice, but not (smoothly) slice (as defined above). These examples give rise to examples of exotic \(\mathbb{R}^4\)'s - manifolds homeomorphic to \(\mathbb{R}^4\), but not diffeomorphic to it.
The notion of sliceness leads to a second equivalence relation on the set of knots:
Two knots \(K_0\) and \(K_1\) are called concordant if the connected sum \(K_0 \# -K_1\) is a slice knot. Here for a knot \(K\), its inverse \(-K\) is the image of \(K\) under an orientation-reversing diffeomorphism of \(S^3\) with the opposite orientation. (To properly define the connected sum operation we should really think of a knot \(K\) as a pair of oriented manifolds \((S^3, S^1)\); then the connected sum of two knots is defined in the standard way for oriented pairs.)
The set of concordance classes of knots forms an abelian group with the group operation induced by connected sum. The unknot represents the identity element while the additive inverse of a concordance class \([K]\) is \([-K]\) (which justifies the name inverse for \(-K\)).
Clearly, isotopic knots are concordant. The converse is in general not true. For example, for any nontrivial (not isotopic to the unknot) knot \(K\) the knot \(K \# -K\) is a nontrivial slice knot.
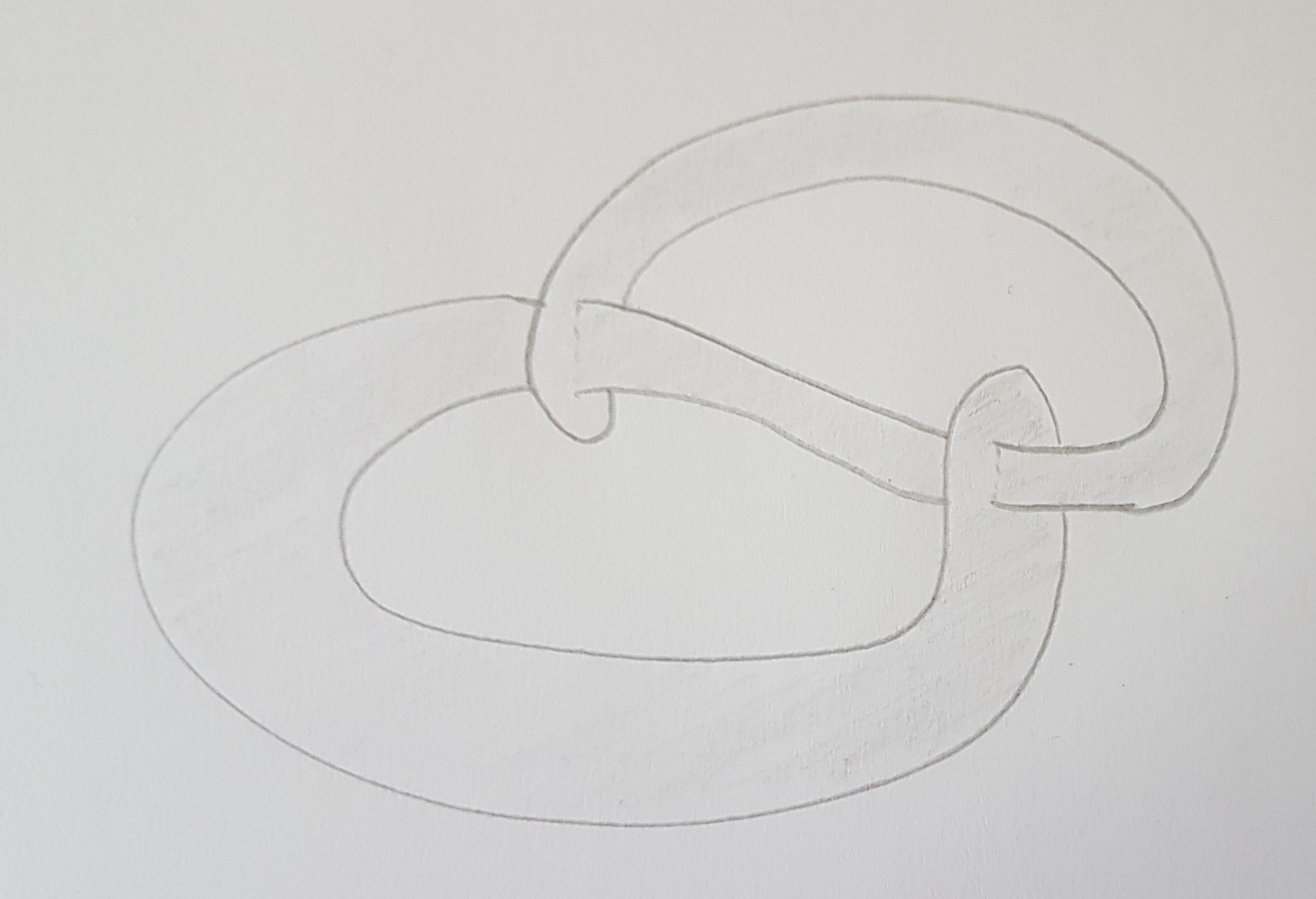
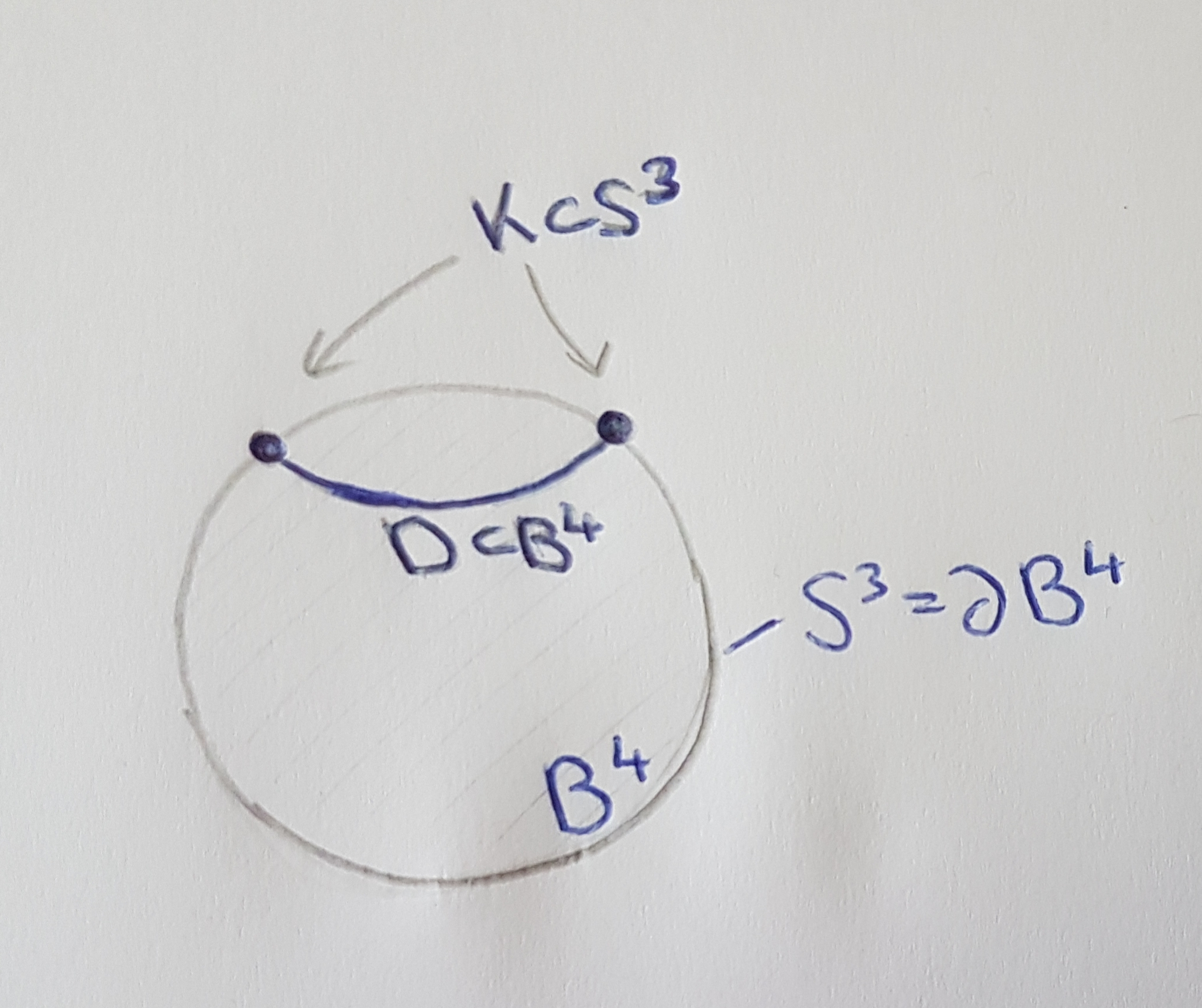
Top: An example of a slice knot, the square knot,
which is the connected sum of the trefoil and its inverse
Bottom: A schematic of a slice knot \(K\) in \(S^3\) bounding a disk in \(B^4\)
Knots as closures of braids
Informally, for \(n \geq 1\), an \(n\)-braid is a collection of \(n\) non-intersecting, unknotted and never-returning paths in 3-dimensional space connecting \(n\) distinguished points to another set of \(n\) distinguished points. Two \(n\)-braids are considered the same if there is an ambient isotopy taking one of them to the other. The braid group on \(n\) strands, denoted \(B_n\), is the group of isotopy classes of \(n\)-braids, where the group operation is given by stacking braids on top of each other and rescaling. The classical presentation for \(B_n\) with generators \(\sigma_1, \ldots, \sigma_{n-1}\) and relations \[ \sigma_i \sigma_j = \sigma_j \sigma_i \quad \text{if } | i-j| \geq 2 \quad \text{and} \quad \sigma_i \sigma_{i+1} \sigma_i = \sigma_{i+1} \sigma_{i} \sigma_{i+1} \quad \text{for } i,j\in \{1,\ldots,n-1\} \] was first introduced by Artin in 1925. The generators \(\sigma_1, \ldots, \sigma_{n-1}\) correspond to the braids that exchange two consecutive of the distinguished points by a half-twist, see the next figure for an example (\(n=3\)).
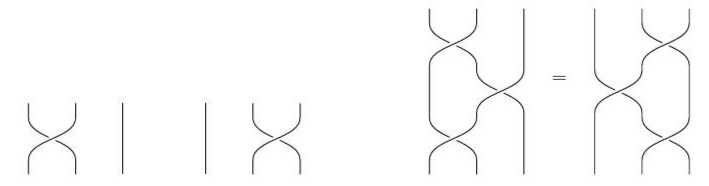
The two generators \(\sigma_1\) and \(\sigma_2\) of the braid group \(B_3\) on the left
and the braid relation \(\sigma_1 \sigma_{2} \sigma_1 = \sigma_{2} \sigma_{1} \sigma_{2} \) in \(B_3\) on the right
By gluing the top ends of the strands to the corresponding bottom ends, we get a knot or link. On the other hand, by a theorem of Alexander, every knot in \(S^3\) can be represented as the closure of an \(n\)-braid for some \(n\geq 1\). So the braid group provides an algebraic/combinatorial tool for examining knots.
I like to study different notions of positivity for braids. A positive braid on \(n\) strands is an \(n\)-braid in the braid group \(B_n\) that can be written as a positive braid word \(\sigma_{s_1} \sigma_{s_2} \cdots \sigma_{s_l}\) with \(s_i \in \{1, \ldots, n-1\}\). An \(n\)-braid is called quasipositive if it is a (finite) product of conjugates of positive Artin generators \(\sigma_i\) of \(B_n\), and it is called strongly quasipositive if the product consists only of certain conjugates of the positive Artin generators. A knot or link is called a (strongly) quasipositive knot if it can be represented as the closure of a (strongly) quasipositive braid, and a positive braid knot if it can be represented as the closure of a positive braid.
Quasipositive knots arise as transverse intersections of smooth algebraic curves in \(\mathbb{C}^2\) with \(S^3 \subset \mathbb{C}^2\), which provides a geometric characterization of these knots by work of Boileau-Orevkov and Rudolph. In the context of smooth concordance, (strongly) quasipositive knots are special. For example, it follows from the slice-Bennequin inequalities due to Bennequin and Rudolph that not every knot is concordant to a quasipositive knot. In arXiv:2210.06612, I show that every strongly quasipositive knot other than the unknot is concordant to infinitely many strongly quasipositive knots.
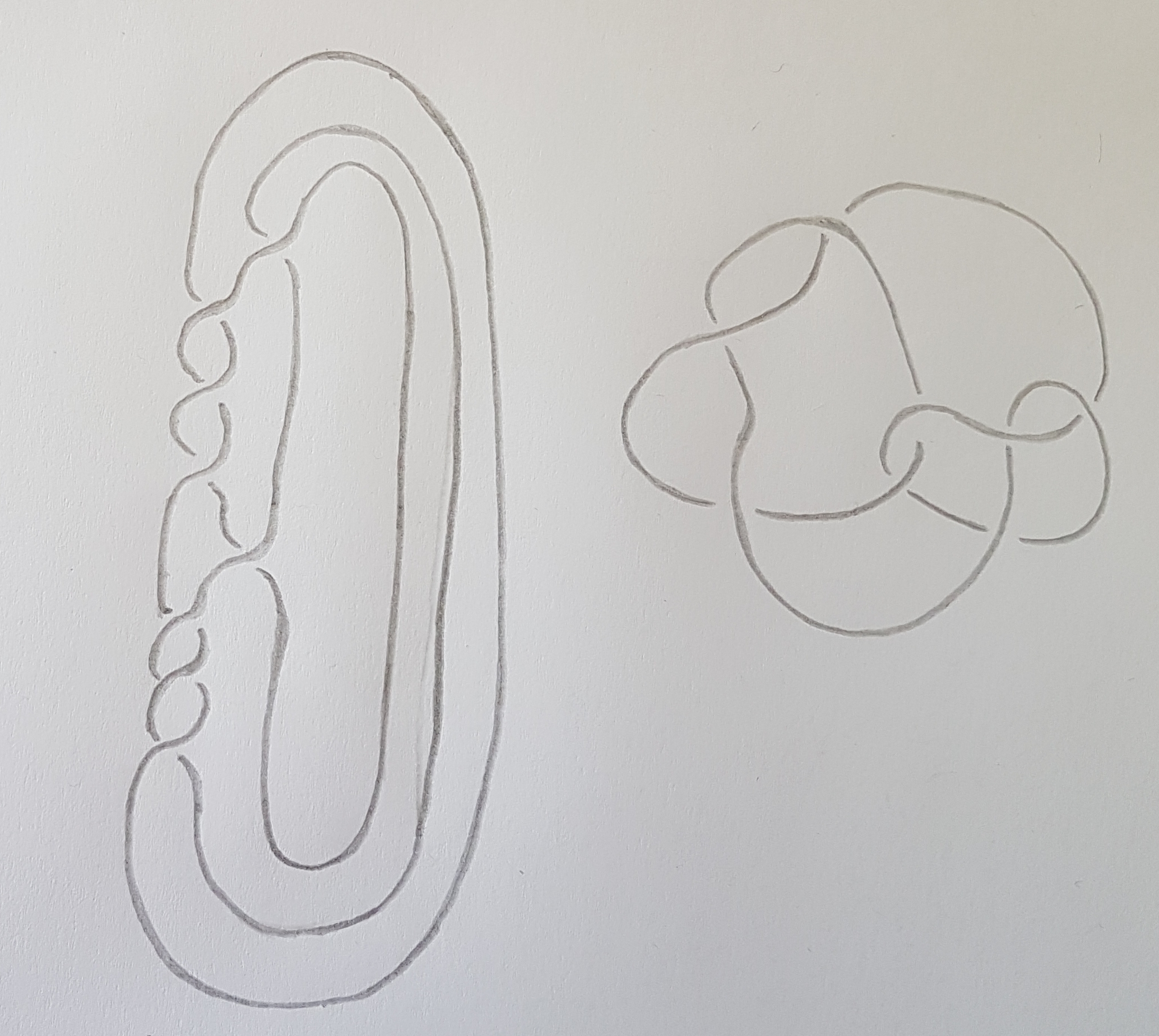
An example of a positive braid knot, \(8_{19}\) in the Rolfsen knot table,
on the left hand side as closure of the braid word \(\sigma_1^3 \sigma_2 \sigma_1^3 \sigma_2\)
