hp2D::NeumannTraceElement< F > Class Template Referenceabstract
Element on an edge representing the normal derivatives of neighbouring elements, especially their mean or jump. More...
#include <neumannTraceElement.hh>
Classes | |
| struct | mapPart |
| class | NTShapeFunction |
Public Types | |
| typedef Real | FieldT |
| enum | intFormType { ZERO, ONE, TWO, THREE } |
| Integration form, which determines terms coming from integration over reference element. More... | |
| typedef Real | type |
| typedef concepts::ElementAndFacette< hp2D::Element< F > > | UnderlyingElement |
Public Member Functions | |
| void | addElement (const hp2D::Quad< Real > &quad, uint k, Real weight=1.0) |
| Adds the contribution to the Neumann trace from the element on one of the (at most two) sides. More... | |
| void | addIrrElement (const hp2D::Quad< Real > &coarseQuad, uint k_coarse, Real weight) |
| Basically the same as addElement, but with the difference in the meaning. More... | |
| void | buildT () |
| After adding the Elements this routine builds the TMatrix and polynomial informations on the element. More... | |
| virtual const concepts::EdgeNd & | cell () const |
| Returns the cell on which the element is built. More... | |
| const concepts::Real3d | chi (const Real x) const |
| Computes the element map. More... | |
| void | computeShpfctVals (const concepts::Array< Real > &xP, concepts::Array< Real > &val) const |
| Evaluation method to get basisfunctions evaluated on requested points this should be used for functions, i.e. More... | |
| Real3d | elemMap (const Real coord_local) const |
| Real3d | elemMap (const Real2d &coord_local) const |
| Real3d | elemMap (const Real3d &coord_local) const |
| virtual const concepts::ElementGraphics< Real > * | graphics () const |
| Returns element graphics class. More... | |
| const concepts::QuadratureRule1d * | integration () const |
| Returns the integration rule. More... | |
| Real | jacobianDeterminant (const Real x) const |
| Computes the determinant of the Jacobian. More... | |
| NeumannTraceElement (const concepts::EdgeNd &cell, uint p, const mapPart *coarseCell=0) | |
| Constructor. More... | |
| ushort | p () const |
| virtual bool | quadraturePoint (uint i, intPoint &p, intFormType form=ZERO, bool localCoord=false) const |
| Delivers a quadrature point. More... | |
| virtual void | recomputeShapefunctions () |
| Recompute shape functions, e.g. More... | |
| virtual const concepts::ShapeFunction1D< Real > * | shpfct () const |
| Returns the shape functions. More... | |
| virtual const concepts::ShapeFunction1D< Real > * | shpfct () const=0 |
| Returns the shape functions. More... | |
| virtual const concepts::Edge & | support () const |
| virtual const concepts::TMatrix< F > & | T () const |
| virtual const TMatrixBase< Real > & | T () const=0 |
| Returns the T matrix of the element. More... | |
| const concepts::Sequence< UnderlyingElement > & | uelm () const |
| Returns the Underlying Element(s) More... | |
| virtual concepts::Real3d | vertex (uint i) const |
| virtual | ~NeumannTraceElement () |
Static Public Member Functions | |
| static concepts::QuadRuleFactory & | rule () |
| Access to the quadrature rule, which is valid for all elements of this type (hp1D::IntegrableElm). More... | |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
Protected Attributes | |
| const concepts::EdgeNd & | cell_ |
| The cell. More... | |
| std::unique_ptr< concepts::QuadratureRule1d > | int_ |
| The integration rule. More... | |
| ushort | p_ |
| T matrix of the element. More... | |
Static Protected Attributes | |
| static std::unique_ptr< LineGraphics > | graphics_ |
| static concepts::QuadRuleFactory | rule_ |
Private Member Functions | |
| void | compute_ (const concepts::Array< Real > &q, concepts::Array< Real > &val) const |
| Routine calculating the normal derivative of the basis functions (of underlying quads), with normalvector pointing outwards the respective underlying Quad on a given Set of Points. More... | |
| void | irregularCompute_ (const concepts::Array< Real > &q, concepts::Array< Real > &val) const |
| Routine calculating the normal derivative of the basis functions (of underlying quads), with normalvector pointing outwards the respective underlying Quad on a given Set of Points. More... | |
Private Attributes | |
| mapPart | coarseCell_ |
| bool | irregular_ |
| std::unique_ptr< concepts::ShapeFunction1D< Real > > | shpfct_ |
| concepts::TMatrix< Real > | T_ |
| concepts::Sequence< UnderlyingElement > | uelm_ |
| concepts::Array< Real > | values_ |
| The actual storage of the values of the shape functions along the edge on integration points. More... | |
| concepts::Sequence< Real > | weights_ |
| Weight for each side. This defines the TraceType on the Element. More... | |
Detailed Description
template<class F = Real>
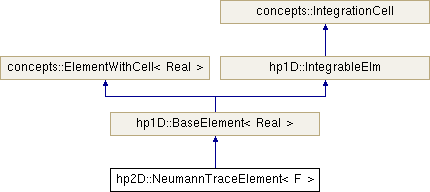
class hp2D::NeumannTraceElement< F >
Element on an edge representing the normal derivatives of neighbouring elements, especially their mean or jump.
Also a PLUS and MINUS setting is involded, that is a FIRST trace kind, with respect to the K+ and K- introduced elements via the setted Normalvector.
The number of shape functions are the sum of the number of shape functions of the two neighbouring 2D elements.
Definition at line 42 of file neumannTraceElement.hh.
Member Typedef Documentation
◆ FieldT
|
inherited |
Definition at line 82 of file element.hh.
◆ type
|
inherited |
Definition at line 81 of file element.hh.
◆ UnderlyingElement
| typedef concepts::ElementAndFacette<hp2D::Element<F> > hp2D::NeumannTraceElement< F >::UnderlyingElement |
Definition at line 44 of file neumannTraceElement.hh.
Member Enumeration Documentation
◆ intFormType
|
inherited |
Integration form, which determines terms coming from integration over reference element.
| Enumerator | |
|---|---|
| ZERO | |
| ONE | |
| TWO | |
| THREE | |
Definition at line 29 of file integral.hh.
Constructor & Destructor Documentation
◆ NeumannTraceElement()
| hp2D::NeumannTraceElement< F >::NeumannTraceElement | ( | const concepts::EdgeNd & | cell, |
| uint | p, | ||
| const mapPart * | coarseCell = 0 |
||
| ) |
Constructor.
For irregular meshes the underlying elements of a neumanntraceelement is a fine Quad and a neighboured coarse Quad. The coarseCell describes the edgemapping of the coarseedge of which the cell is a subset (part). The coarseCellpart also marks if a neumanntraceElement is build upon regular or irregular mesh
- Parameters
-
cell geometric cell of this element p highest Polynomial degree of underlying Elements coarseCell for irregular meshes where cell's underlying
◆ ~NeumannTraceElement()
|
virtual |
Member Function Documentation
◆ addElement()
| void hp2D::NeumannTraceElement< F >::addElement | ( | const hp2D::Quad< Real > & | quad, |
| uint | k, | ||
| Real | weight = 1.0 |
||
| ) |
Adds the contribution to the Neumann trace from the element on one of the (at most two) sides.
Basis functions between quads do not have to be continous. In this case the highest polynomial degree along edge is set, i.e. for integration rule
- Parameters
-
quad Quad with k-th edge is NeumannTraceElement's topological cell.
◆ addIrrElement()
| void hp2D::NeumannTraceElement< F >::addIrrElement | ( | const hp2D::Quad< Real > & | coarseQuad, |
| uint | k_coarse, | ||
| Real | weight | ||
| ) |
Basically the same as addElement, but with the difference in the meaning.
In this case the general ancestor edge of this finer Edge is the k-th edge of the coarseQuad.
- Parameters
-
coarseQuad Quad with k-th edge is general ancestor of NeumannTraceElement's topological cell.
◆ buildT()
| void hp2D::NeumannTraceElement< F >::buildT | ( | ) |
After adding the Elements this routine builds the TMatrix and polynomial informations on the element.
◆ cell()
|
inlinevirtualinherited |
Returns the cell on which the element is built.
Implements concepts::ElementWithCell< Real >.
Definition at line 99 of file element.hh.
◆ chi()
|
inlineinherited |
◆ compute_()
|
private |
Routine calculating the normal derivative of the basis functions (of underlying quads), with normalvector pointing outwards the respective underlying Quad on a given Set of Points.
- Parameters
-
q evaluation domain points val of evaluations of shapefunctions on q values
◆ computeShpfctVals()
| void hp2D::NeumannTraceElement< F >::computeShpfctVals | ( | const concepts::Array< Real > & | xP, |
| concepts::Array< Real > & | val | ||
| ) | const |
Evaluation method to get basisfunctions evaluated on requested points this should be used for functions, i.e.
- Parameters
-
xP requested Points to evaluate on val evaluated shpfct, method resizes array.
◆ elemMap() [1/3]
|
inlineinherited |
Definition at line 86 of file element.hh.
◆ elemMap() [2/3]
|
inlineinherited |
Definition at line 90 of file element.hh.
◆ elemMap() [3/3]
|
inlineinherited |
Definition at line 94 of file element.hh.
◆ graphics()
|
virtualinherited |
Returns element graphics class.
◆ info()
|
protectedvirtual |
Reimplemented from hp1D::BaseElement< Real >.
◆ integration()
|
inlineinherited |
Returns the integration rule.
Definition at line 51 of file element.hh.
◆ irregularCompute_()
|
private |
Routine calculating the normal derivative of the basis functions (of underlying quads), with normalvector pointing outwards the respective underlying Quad on a given Set of Points.
This is for irregular underlying elements
- Parameters
-
q evaluation domain points val of evaluations of shapefunctions on q values
◆ jacobianDeterminant()
|
inlineinherited |
Computes the determinant of the Jacobian.
Definition at line 45 of file element.hh.
◆ p()
|
inlineinherited |
Definition at line 103 of file element.hh.
◆ quadraturePoint()
|
virtualinherited |
Delivers a quadrature point.
Quadrature point consists of coordinates (for evaluation of formulas) and intermediate data, consisting of the weight and term coming from mapping.
Returns false, if the number of quadrature points is overstepped.
- Parameters
-
i number of quadrature point intPoint data given back form Integration form localCoord If true, local coordinates are returned. Else physical coordinates.
Implements concepts::IntegrationCell.
◆ recomputeShapefunctions()
|
virtual |
Recompute shape functions, e.g.
for other abscissas redefined through IntegrableElm::rule().set(...)
Implements hp1D::BaseElement< Real >.
◆ rule()
|
inlinestaticinherited |
Access to the quadrature rule, which is valid for all elements of this type (hp1D::IntegrableElm).
Change of the quadrature rule is put into practice for newly created elements and for already created elements by precomputing the integration points and shape functions on them.
Definition at line 62 of file element.hh.
◆ shpfct() [1/2]
|
virtual |
Returns the shape functions.
◆ shpfct() [2/2]
|
pure virtualinherited |
Returns the shape functions.
◆ support()
|
inlinevirtualinherited |
Definition at line 91 of file element.hh.
◆ T() [1/2]
|
inlinevirtual |
Definition at line 121 of file neumannTraceElement.hh.
◆ T() [2/2]
|
pure virtualinherited |
Returns the T matrix of the element.
Implemented in hp3D::Element< Real >, and hp2D::Element< Real >.
◆ uelm()
|
inline |
Returns the Underlying Element(s)
Definition at line 151 of file neumannTraceElement.hh.
◆ vertex()
|
inlinevirtualinherited |
Definition at line 95 of file element.hh.
Member Data Documentation
◆ cell_
|
protectedinherited |
The cell.
Definition at line 70 of file element.hh.
◆ coarseCell_
|
private |
Definition at line 190 of file neumannTraceElement.hh.
◆ graphics_
|
staticprotectedinherited |
Definition at line 126 of file element.hh.
◆ int_
|
protectedinherited |
The integration rule.
Definition at line 72 of file element.hh.
◆ irregular_
|
private |
Definition at line 188 of file neumannTraceElement.hh.
◆ p_
|
protectedinherited |
T matrix of the element.
Definition at line 124 of file element.hh.
◆ rule_
|
staticprotectedinherited |
Definition at line 74 of file element.hh.
◆ shpfct_
|
mutableprivate |
Definition at line 179 of file neumannTraceElement.hh.
◆ T_
|
private |
Definition at line 182 of file neumannTraceElement.hh.
◆ uelm_
|
private |
Definition at line 192 of file neumannTraceElement.hh.
◆ values_
|
mutableprivate |
The actual storage of the values of the shape functions along the edge on integration points.
The values corresponding to the local shapefunctions of its underlying quad(s) are computed with the normalvector pointing outwards the quad respectivly.
This have to be noticed for defining the weights for trace types. mutable to work with const compute_ as needed for const
Definition at line 201 of file neumannTraceElement.hh.
◆ weights_
|
private |
Weight for each side. This defines the TraceType on the Element.
Definition at line 204 of file neumannTraceElement.hh.
The documentation for this class was generated from the following file:

