elasticity2D_tutorial.cc
Contents
- Introduction
- Reduction to 2-dimensional elasticity
- Variational Formulation
- Commented Program
- Results
- Complete Source Code
Introduction
In this tutorial the implementation of linear elasticity problems in 2D is shown. We consider a thin plate with a hole at its centre. The plate is fixed at its left face and and there is some applied force on its right face. This is shown in the following figure.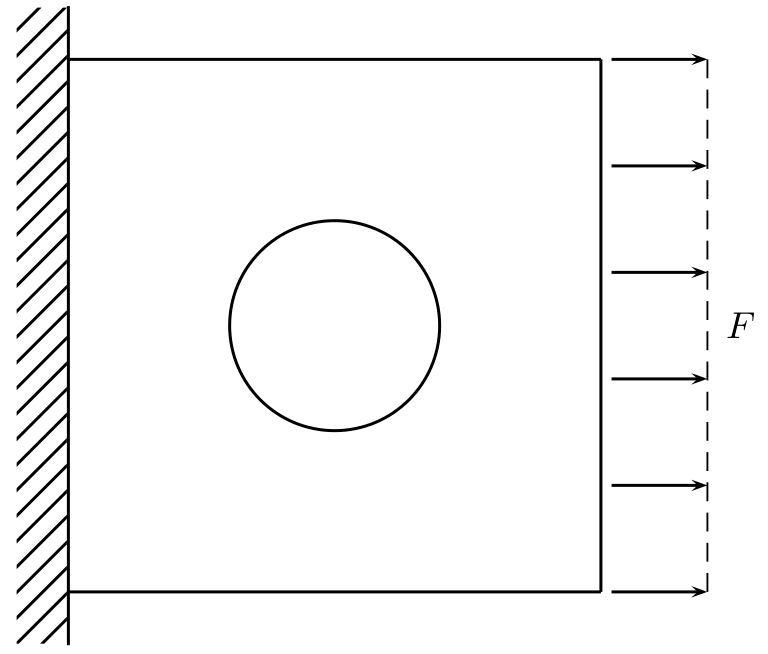 
First we will give a short overview of the equations of linear elasticity in three dimensions and then reduce the problem to two dimensions.
The equation to be solved is
![\[ - {\rm div} \:\sigma(u) = f \quad \text{in } \Omega, \]](form_73.png)
for the unknown displacement 
where 
.
The applied body forces are described by the mapping 
, called the density of the applied body force per unit volume. The tensor 
is the stress tensor, which will be described later.
On a subset 
the body is fixed and we get the homogenous Dirichlet boundary condition
![\[ u = 0 \quad \text{on } \Gamma_0. \]](form_79.png)
On the subset 
we have applied surface forces, which are given by a mapping 
, called the density of the applied surface force per unit area. From that we get the boundary condition
![\[ \sigma(u) n = g \quad \text{on } \Gamma_1, \]](form_82.png)
where 
is the unit outer normal vector along 
.
The linear stress tensor is given by (also known as Hooke's Law)
![\[ \sigma(u) = \lambda\; {\rm trace} (\varepsilon(u)) + 2\mu \varepsilon(u). \]](form_85.png)
with the linear strain tensor
![\[ \varepsilon_{ij}(u) = \frac{1}{2} (\partial_j u_i + \partial_i u_j ). \]](form_86.png)
Reduction to 2-dimensional elasticity
For the reduction to a 2-dimensional problem there are two kinds of reduction techniques: the plane stress state and the plane strain state. The plane stress state is a good approximation for very thin bodies. In this case one can assume that all components of connected to the 
-direction vanish, i.e.
![\[ \sigma_{i3}(u) = \sigma_{3i}(u) = 0 \quad i=1,2,3. \]](form_88.png)
By throwing away the component of 
in the -direction and expressing 
by 
and 
, we can write the material law from the first section in the form
![\[ \sigma^{\rm 2D} (u) = 2\mu \frac{\lambda}{\lambda+2\mu}\; {\rm trace}\left(\varepsilon^{\rm 2D}(u)\right) + 2\mu \varepsilon^{\rm 2D}(u). \]](form_92.png)
For the plane strain state one can assume that all components of 
connected to the -direction vanish. Again by throwing away the component of in the -direction one can then write the material law in the form
![\[ \sigma^{\rm 2D} (u) = \lambda\; {\rm trace}\left(\varepsilon^{\rm 2D}(u)\right) + 2\mu \varepsilon^{\rm 2D}(u). \]](form_94.png)
Here we will use the plane stress state.
Variational Formulation
We choose
![\[ V := \{ v \in H^1(\Omega)^2\,|\,\text{with } v = 0 \text{ on } \Gamma_0 \} \]](form_95.png)
where now 
. Then we have the bilinearform
![\[ B(u,v) = \int_\Omega \sigma^{\rm 2D}(u):\varepsilon^{\rm 2D}(v) \;{\rm d}x \]](form_97.png)
with 
. Here we use for matrices 
.
Finally, the variational formulation is: Find 
such that
![\[ 2\mu \frac{\lambda}{\lambda+2\mu} \int_\Omega {\rm div}(u){\rm div}(v) \;{\rm d}x + 2\mu \int_\Omega \varepsilon^{\rm 2D}(u): \varepsilon^{\rm 2D}(v) \;{\rm d}x = \int_\Omega f \cdot v \;{\rm d}x + \int_{\Gamma_1} g \cdot v \;{\rm d}s \quad \forall v \in V \]](form_101.png)
in the case of the plane stress state and
![\[ \lambda \int_\Omega {\rm div}(u){\rm div}(v) \;{\rm d}x + 2\mu \int_\Omega \varepsilon^{\rm 2D}(u): \varepsilon^{\rm 2D}(v) \;{\rm d}x = \int_\Omega f \cdot v \;{\rm d}x + \int_{\Gamma_1} g \cdot v \;{\rm d}s \quad \forall v \in V \]](form_102.png)
in the case of the plane strain state. We will use this splitting of the bilinear form for computing the system matrix later.
Commented Program
First, systemfiles
and conceptfiles
are included. In this example we use a cig-file as input. This file is create with a Python script and contains geometry data, the densities of the applied forces, material constants and values for the h- and p-refinement. For using that cig-file as input, we write a method that first sets some default values and then reads the file.
We first read the input data from the cig-file
and save the material constants and the applied forces (each component is one function) for better access in some variables.
Then the mesh is generated and we write the mesh to an eps-file.
We load the attribute of the edges with the Dirichlet boundary condition from the input file and set the boundary condition for all edges with this attribute.
Now we first create a scalar space for the several components of the solution and save it again in an eps-file.
We can then put this space into the components of the vectorial space.
We create a trace space for the Neumann boundary condition.
Now, we can compute the system matrix, where we use the splitted form of the bilinear form as stated in the variational formulation of the problem.
The right hand side vectors are computed from the applied volume and surface forces. We compute these vectors for each component of the forces and concatenate them to one vector for the vectorial system.
We solve the system with a direct method provided by SuperLU.
For better access and post-processing we split the solution into the two parts 
and 
.
Now we write the solution (the displacement) and the resulting strains and stresses to a matlab binary file. Before doing that we recompute the shape functions on equidistant points.
We compute the energy norm of the solution.
Finally, exceptions are caught and a return value is given back.
Results
For running this project we first have to create the cig file with the python script
With a symbolic link named bin to the directory containing the binaries, we can start the program with
The output of the program on the screen is then
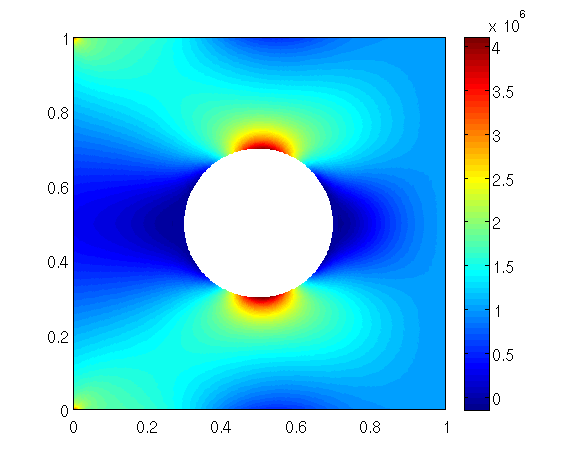
The output of the solutions of the program is saved in a file called elasticity2D_stress.mat. For regarding the output (for example the stress 
) in MATLAB we can type the following in the MATLAB command window
This creates the following image. 