|
| virtual void | apply_ () |
| | Intrinsic application method without argument. More...
|
| |
| virtual void | apply_ (const Vector< F > &fncY, Vector< F > &fncX) |
| | Intrinsic application method, i.e. More...
|
| |
| virtual const uint | dimX () const |
| | Returns the size of the image space of the operator (number of rows of the corresponding matrix) More...
|
| |
| virtual const uint | dimY () const |
| | Returns the size of the source space of the operator (number of columns of the corresponding matrix) More...
|
| |
| virtual void | hide_messages () |
| |
| | Mumps (const int rank, const int comm=-987654) |
| | Empty constructor for the parallel version. More...
|
| |
| | Mumps (const Operator< F > &A, const bool symmetric, const int rank=-1, const int comm=-987654) |
| | Constructor. More...
|
| |
| | Mumps (const Operator< F > &A, const int rank=-1, const int comm=-987654) |
| | Constructor. More...
|
| |
| void | operator() () |
| | Application method without second argument. Used for parallel solvers. More...
|
| |
| virtual void | operator() (const Function< c_type > &fncY, Function< c_type > &fncX) |
| | Application operator for complex function fncY. More...
|
| |
| virtual void | operator() (const Function< r_type > &fncY, Function< F > &fncX) |
| | Application operator for real function fncY. More...
|
| |
| void | operator() (const Matrix< c_type > &mX, Matrix< c_type > &mY) |
| | Application method to complex matrices. Calls apply_() More...
|
| |
| void | operator() (const Matrix< r_type > &mX, Matrix< F > &mY) |
| | Application method to real matrices. Calls function apply() More...
|
| |
| virtual void | operator() (const Vector< c_type > &fncY, Vector< c_type > &fncX) |
| | Application operator for complex function fncY. More...
|
| |
| virtual void | operator() (const Vector< r_type > &fncY, Vector< F > &fncX) |
| | Application operator for real vector fncY. More...
|
| |
| virtual void | show_messages () |
| |
| virtual | ~Mumps () |
| | Destructor. More...
|
| |
template<class F>
class concepts::Mumps< F >
MUMPS : MUltifrontal Massively Parallel sparse direct Solver.
MUMPS is a general purpose library for the direct solution of large, sparse, nonsymmetric systems of linear equations on high perormances machines, for both real and complex matrices. The library routines will perform an partial factorization and Schur complement matrix (centralized or 2D block-cyclic).
MUMPS offers different ordering options for a column permutation 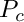 .
.
MUMPS has also parallel implementation.
- Warning
- If MUMPS was compiled with MPI, then Concepts should be compiled with MPI as well (even if using one single node during the execution). As well, the C++ main function code should start with and end with
MPI::Finalize();
return 0;
- Author
- Patrick Amestoy
-
Alfredo Buttari
-
Abdou Guermouche
-
Jean-Yves L'Excellent
-
Bora Ucar
- See also
- homepage of MUMPS
-
P.R. Amestoy, I.S. Duff and J.-Y. L'Excellent, Multifrontal parallel distributed symmetric and unsymmetric solvers.Revised version appeared in Comput. Methods in Appl. Mech. Eng., 184, 501-520 (2000).
- Examples
- BGT_0.cc, elasticity2D_tutorial.cc, exactDtN.cc, and inhomDirichletBCsLagrange.cc.
Definition at line 72 of file mumps.hh.
Application operator for complex function fncY.
Computes fncX = A(fncY) where A is this operator. fncX becomes complex.
In derived classes its enough to implement the operator() for complex Operator's. If a real counterpart is not implemented, the function fncY is splitted into real and imaginary part and the application operator for real functions is called for each. Then the result is combined.
If in a derived class the operator() for complex Operator's is not implemented, a exception is thrown from here.
Reimplemented from concepts::Operator< F >.
Application operator for real function fncY.
Computes fncX = A(fncY) where A is this operator.
fncX becomes the type of the operator, for real data it becomes real, for complex data it becomes complex.
In derived classes its enough to implement the operator() for real Operator's. If a complex counterpart is not implemented, the function fncY is transformed to a complex function and then the application operator for complex functions is called.
If in a derived class the operator() for real Operator's is not implemented, a exception is thrown from here.
Reimplemented from concepts::Operator< F >.
Application operator for complex function fncY.
Computes fncX = A(fncY) where A is this operator. fncX becomes complex.
In derived classes its enough to implement the operator() for complex Operator's. If a real counterpart is not implemented, the vector fncY is splitted into real and imaginary part and the application operator for real vectors is called for each. Then the result is combined
If in a derived class the operator() for complex Operator's i not implemented, a exception is thrown from here.
Application operator for real vector fncY.
Computes fncX = A(fncY) where A is this operator.
Type of fncX becomes that of the operator, for real data it becomes real, for complex data it becomes complex.
In derived classes its enough to implement the operator() for real Operator's. If a complex counterpart is not implemented, the vector fncY is transformed to a complex vector and then the application for complex vectors is called.
If in a derived class the operator() for real Operator's is not implemented, a exception is thrown from here.

![]() .
.
