inhomDirichletBCsLagrange.cc

Contents

1. Introduction
2. Variational Formulation
3. Commented Program
4. Results
5. Complete Source Code

@section intro Introduction
In this tutorial the implementation of inhomogeneous Dirichlet boundary 
conditions using Lagrangian multipliers is shown.

The equation solved is the reaction-diffusion equation
\f[ - \Delta u + u = f \f]
in the unit square \f$ \Omega = (0,1)^2 \f$ with source term
\f[
f(x,y) = -5\exp\left(-(x-1/2)^2-(y-1/2)^2\right)
\f]
and Dirichlet boundary condition
\f$
u = g
\f$
on the boundary \f$ \partial\Omega \f$ of \f$ \Omega \f$ where
\f[
g = 
\begin{cases}
\sin \pi x, &(x,y)\in\Gamma_{\rm inh}=\{(x,y)\in\partial\Omega\mid y=0\},\\
0,          &(x,y)\in\partial\Omega\setminus\Gamma_{\rm inh}.
\end{cases}
\f]

@section variation Variational Formulation
The variational formulation of the reaction-diffusion equation reads: find 
\f$ u \in H^1(\Omega) \f$ that satisfies the boundary conditions and
\f[
\int_{\Omega}\nabla u\cdot\nabla v\;{\rm d}x
+ \int_{\Omega} u\,v\;{\rm d}x
- \int_{\partial\Omega} \partial_n u \,v \;{\rm d}s(x)
= 
\int_{\Omega} f\,v\;{\rm d}x,
\f]
for all \f$ v \in H^1(\Omega) \f$. In order to incorporate the boundary
conditions into the variational formulation, we introduce the Lagrangian
multiplier \f$ \lambda \in H^{-1/2}(\partial\Omega) \f$ defined by
\f$ \lambda = \partial_n u \f$. The space \f$ H^{-1/2}(\partial\Omega) \f$
of the Lagrangian multiplier is the dual space of the trace space 
\f$ H^{1/2}(\partial\Omega) \f$ of \f$ H^1(\Omega) \f$ on the boundary 
\f$ \partial\Omega \f$. The boundary condition is then incorporated by
testing the condition with test functions in the dual space
\f$ H^{-1/2}(\partial\Omega) \f$. Thus, the mixed variational formulation
reads: find \f$ (u,\lambda)\in H^1(\Omega) \times H^{-1/2}(\partial\Omega) \f$
such that
\f{eqnarray*}{
  \int_{\Omega}\nabla u\cdot\nabla v\;{\rm d}x
+   \int_{\Omega} uv\;{\rm d}x
-   \int_{\partial\Omega} \lambda \,v \;{\rm d}s(x)
&=& \int_{\Omega} f\,v\;{\rm d}x
\qquad\forall v\in H^1(\Omega)\\
\int_{\partial\Omega} u \lambda' \;{\rm d}s(x)
&=& \int_{\partial\Omega} g \lambda' \;{\rm d}s(x)
\qquad\forall \lambda'\in H^{-1/2}(\partial\Omega)
\f}

@dontinclude inhomDirichletBCsLagrange.cc
@section commented Commented Program
First, system files
@until iostream
and concepts files
@until toolbox
are included. With the following using directive
@until using
we do not need to prepend <tt>concepts::</tt> to <tt>Real</tt> everytime.

@subsection main Main Program
The mesh is read from three files containing the coordinates, the
elements and the boundary attributes of the mesh.
@until endl
<!--Please see the tutorial @ref mesh "Import 2D Mesh" for a concise explanation of how to write these import files and define the attributes for edges etc. -->
In our example the edges are given the following attributes: 1 (bottom), 2 (right), 3 (top) and 4 (left).

Now the mesh is plotted using a scaling factor of 100, a greyscale of 1.0 
and one point per edge.
@until drawMeshEPS

We define a set of attributes of the boundary edges
@skip concepts
@until insert

The space is built using the mesh, a refinement factor of 2 and a 
polynomial degree to 3. Then the elements of the space are built
and the space is plotted.
@skip hp2D
@until drawMeshEPS

Now we build the trace space of our space at the boundary edges 
@skip hp2D
@until endl
and its corresponding dual space.
@until endl

The right hand side is computed. First we calculate the vector corresponding
to the linear form of the source term
@skip hp2D
@until endl
then the vector that corresponds to the inhomogeneous Dirichlet boundary
condition is built
@until endl
and finally, these two vectors are put together in a block vector.
@until endl

The system matrix is also assembled as a block matrix. First we account for
the bilinear forms \c hp2D::Laplace<Real> and \c hp2D::Identity<Real> that
build the upper right block.
@skip hp2D
@until endl
@until endl
Then the bilinear form \c hp1D::Identity<Real> is used to build the remaining
two rectangular block matrices \c M12 and \c M21 that correspond to the
boundary conditions.
@until endl
@until endl
Finally, the four precomputed matrices \c A11, \c M11, \c A12 and \c A21 are
added into the block system matrix \c A.
@until endl

We solve the equation using the iterative solver CG.
@skip concepts
@until endl

The coefficient vector \c u of the solution and the coefficient vector \c lambda
of the Lagrangian are read from the solution vector \c sol.
@skip concepts
@until endl
@until endl

Finally, the solution \c u is plotted using <tt>graphics::MatlabGraphics</tt>.
To this end the shape functions are computed on equidistant points using the 
trapezoidal quadrature rule.
@skip hp2D
@until MatlabGraphics

Finally, exceptions are caught and a sane return value is given back.
@until }
@until }

@section results Results
Output of the program:
@code 

Mesh: Import2dMesh(ncell = 1)

Space: hpAdaptiveSpaceH1(dim = 169 (V:25, E:80, I:64), nelm = 16)

Trace Space: TraceSpace(QuadEdgeFirst(), dim = 169, nelm = 16)

Dual Space: DualSpace(dim = 48, nelm = 16)

RHS Vector 2D: Vector(169, [-5.494815e-02, -1.219900e-01, -2.708292e-01, -1.219900e-01, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -4.203145e-02, -1.570171e-03, -1.893229e-02, -7.072544e-04, -6.523089e-03, -2.436833e-04, -2.436833e-04, -9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, -9.199187e-05, -3.436544e-06, -3.061031e-01, -2.879265e-01, -5.059520e-02, -6.301685e-04, -5.059520e-02, -6.301685e-04, -4.759082e-02, 5.927486e-04, -8.362783e-03, -1.041593e-04, -1.041593e-04, -1.297316e-06, -1.296912e-01, -4.468487e-02, -1.669295e-03, -2.143641e-02, -2.669927e-04, -7.385877e-03, -9.199187e-05, -2.759145e-04, -3.436544e-06, -1.219900e-01, -2.708292e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, 9.199187e-05, 3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, -2.436833e-04, 2.436833e-04, 9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -9.199187e-05, 2.759145e-04, 3.436544e-06, -5.059520e-02, -6.301685e-04, -8.362783e-03, -1.041593e-04, 1.041593e-04, 1.297316e-06, -2.708292e-01, -2.879265e-01, -4.759082e-02, 5.927486e-04, -4.759082e-02, 5.927486e-04, -5.059520e-02, -6.301685e-04, -8.362783e-03, 1.041593e-04, 1.041593e-04, -1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 9.199187e-05, 2.759145e-04, -3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, 2.436833e-04, 2.436833e-04, -9.103287e-06, -1.296912e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -7.385877e-03, 2.759145e-04, 9.199187e-05, -3.436544e-06, -2.708292e-01, -1.219900e-01, -4.759082e-02, 5.927486e-04, -4.203145e-02, -1.570171e-03, -2.143641e-02, 2.669927e-04, -7.385877e-03, 9.199187e-05, -2.759145e-04, 3.436544e-06, -4.759082e-02, 5.927486e-04, -8.362783e-03, 1.041593e-04, -1.041593e-04, 1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 2.759145e-04, -9.199187e-05, 3.436544e-06, -5.494815e-02, -1.893229e-02, 7.072544e-04, -1.893229e-02, 7.072544e-04, -6.523089e-03, 2.436833e-04, -2.436833e-04, 9.103287e-06])

RHS Vector 1D: Vector(48, [ 1.960099e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, 1.570060e-02, 5.980456e-03, 2.620727e-01, 3.790460e-02, 2.477186e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, 3.790460e-02, -2.477186e-03, 1.960099e-03, 2.864357e-17, 4.985380e-18, -7.797024e-20, 1.570060e-02, -5.980456e-03, 2.192284e-17, 4.226401e-18, -2.220405e-19, 1.186456e-17, 2.823991e-18, -3.323070e-19, 1.506967e-19, 1.134717e-17, 9.613844e-19, 3.661973e-19, 9.916538e-19, -3.919829e-19, 1.604733e-17, 2.320987e-18, 1.516839e-19, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.134717e-17, 2.320987e-18, -1.516839e-19, 1.200215e-19, 0.000000e+00, 0.000000e+00, 9.613844e-19, -3.661973e-19])

RHS Vector: Vector(217, [-5.494815e-02, -1.219900e-01, -2.708292e-01, -1.219900e-01, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -4.203145e-02, -1.570171e-03, -1.893229e-02, -7.072544e-04, -6.523089e-03, -2.436833e-04, -2.436833e-04, -9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, -9.199187e-05, -3.436544e-06, -3.061031e-01, -2.879265e-01, -5.059520e-02, -6.301685e-04, -5.059520e-02, -6.301685e-04, -4.759082e-02, 5.927486e-04, -8.362783e-03, -1.041593e-04, -1.041593e-04, -1.297316e-06, -1.296912e-01, -4.468487e-02, -1.669295e-03, -2.143641e-02, -2.669927e-04, -7.385877e-03, -9.199187e-05, -2.759145e-04, -3.436544e-06, -1.219900e-01, -2.708292e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, 9.199187e-05, 3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, -2.436833e-04, 2.436833e-04, 9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -9.199187e-05, 2.759145e-04, 3.436544e-06, -5.059520e-02, -6.301685e-04, -8.362783e-03, -1.041593e-04, 1.041593e-04, 1.297316e-06, -2.708292e-01, -2.879265e-01, -4.759082e-02, 5.927486e-04, -4.759082e-02, 5.927486e-04, -5.059520e-02, -6.301685e-04, -8.362783e-03, 1.041593e-04, 1.041593e-04, -1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 9.199187e-05, 2.759145e-04, -3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, 2.436833e-04, 2.436833e-04, -9.103287e-06, -1.296912e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -7.385877e-03, 2.759145e-04, 9.199187e-05, -3.436544e-06, -2.708292e-01, -1.219900e-01, -4.759082e-02, 5.927486e-04, -4.203145e-02, -1.570171e-03, -2.143641e-02, 2.669927e-04, -7.385877e-03, 9.199187e-05, -2.759145e-04, 3.436544e-06, -4.759082e-02, 5.927486e-04, -8.362783e-03, 1.041593e-04, -1.041593e-04, 1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 2.759145e-04, -9.199187e-05, 3.436544e-06, -5.494815e-02, -1.893229e-02, 7.072544e-04, -1.893229e-02, 7.072544e-04, -6.523089e-03, 2.436833e-04, -2.436833e-04, 9.103287e-06, 1.960099e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, 1.570060e-02, 5.980456e-03, 2.620727e-01, 3.790460e-02, 2.477186e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, 3.790460e-02, -2.477186e-03, 1.960099e-03, 2.864357e-17, 4.985380e-18, -7.797024e-20, 1.570060e-02, -5.980456e-03, 2.192284e-17, 4.226401e-18, -2.220405e-19, 1.186456e-17, 2.823991e-18, -3.323070e-19, 1.506967e-19, 1.134717e-17, 9.613844e-19, 3.661973e-19, 9.916538e-19, -3.919829e-19, 1.604733e-17, 2.320987e-18, 1.516839e-19, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.134717e-17, 2.320987e-18, -1.516839e-19, 1.200215e-19, 0.000000e+00, 0.000000e+00, 9.613844e-19, -3.661973e-19])

System Matrix A11: SparseMatrix(169x169, HashedSparseMatrix: 1785 (6.249781e+00%) entries bound.)

System Matrix M11: SparseMatrix(169x169, HashedSparseMatrix: 2809 (9.835090e+00%) entries bound.)

System Matrix M12: SparseMatrix(169x48, HashedSparseMatrix: 176 (2.169625e+00%) entries bound.)

System Matrix M21: SparseMatrix(48x169, HashedSparseMatrix: 176 (2.169625e+00%) entries bound.)

System Matrix A: SparseMatrix(217x217, HashedSparseMatrix: 3161 (6.712820e+00%) entries bound.)

Solver: SuperLU(n = 217)

Solution u: Vector(169, [-4.618187e-05, 7.069643e-01, 1.145203e-01, -6.737844e-06, 1.167766e-01, 1.862732e-02, -2.470489e-01, 1.514000e-02, -3.519155e-02, 1.221787e-02, 1.322993e-04, -6.902704e-05, -1.013099e-01, 1.669996e-02, 9.617324e-03, -6.654778e-03, 9.998063e-01, 1.865285e-01, 2.816255e-01, 7.735581e-03, -3.291444e-01, 1.855298e-02, 6.508634e-02, -4.285469e-03, -8.267659e-02, 4.223839e-03, -1.211792e-03, 4.226654e-04, -1.390862e-01, -1.183708e-01, -1.754974e-01, 7.990149e-03, -2.460012e-02, 2.422257e-03, -1.271327e-01, -5.897882e-03, -4.730098e-02, 2.066261e-03, -6.101182e-04, -3.198163e-05, -9.830384e-07, -7.962944e-02, 6.483805e-03, 1.930221e-05, -1.007091e-05, -2.789381e-02, 1.578405e-03, -3.093302e-03, 2.653529e-04, 7.069643e-01, 1.145203e-01, 2.816255e-01, -7.735581e-03, -2.470489e-01, 1.514000e-02, 6.508634e-02, -4.285469e-03, -8.267659e-02, 4.223839e-03, 1.211792e-03, -4.226654e-04, -4.618187e-05, -6.737844e-06, 1.167766e-01, -1.862732e-02, 1.322993e-04, -6.902704e-05, -3.519155e-02, 1.221787e-02, -1.013099e-01, 1.669996e-02, -9.617324e-03, 6.654778e-03, -9.830383e-07, -1.183708e-01, 1.930221e-05, -1.007091e-05, -7.962944e-02, 6.483805e-03, -1.271327e-01, -5.897882e-03, -2.789381e-02, 1.578405e-03, 3.093302e-03, -2.653529e-04, -2.460012e-02, 2.422257e-03, -4.730098e-02, 2.066261e-03, 6.101182e-04, 3.198163e-05, -1.455751e-01, -1.813026e-01, -8.576158e-02, 1.351182e-03, -3.808927e-02, -1.479655e-03, -1.169898e-01, -2.261237e-03, -3.094099e-02, 7.817582e-04, 1.732044e-04, -1.052190e-04, -1.434247e-07, 2.816158e-06, -1.469324e-06, -7.793823e-02, 5.447240e-03, -2.108433e-02, -3.723651e-04, 2.050604e-03, 1.021590e-04, -2.093464e-08, -3.117919e-09, 4.108983e-07, -2.143576e-07, 6.013141e-08, -3.117924e-08, -9.353940e-02, 2.845042e-03, -7.477594e-02, -1.400725e-02, -1.402879e-02, -7.227994e-03, -8.908596e-10, 1.002195e-08, -3.897302e-09, -1.120371e-01, 1.162164e-03, -1.943360e-02, 1.840847e-03, -6.726515e-04, 1.466207e-04, -1.455751e-01, -1.434247e-07, -8.576158e-02, 1.351182e-03, -7.793823e-02, 5.447240e-03, 2.816158e-06, -1.469324e-06, -2.108433e-02, -3.723651e-04, -2.050604e-03, -1.021590e-04, -3.808927e-02, -1.479655e-03, -3.094099e-02, 7.817582e-04, -1.732044e-04, 1.052190e-04, -3.117930e-09, 1.002198e-08, 3.897372e-09, -9.353940e-02, 2.845042e-03, -1.943360e-02, 1.840847e-03, 6.726515e-04, -1.466207e-04, -2.093467e-08, 6.013149e-08, 3.117930e-08, 4.108985e-07, -2.143576e-07, -7.477594e-02, -1.400725e-02, 1.402879e-02, 7.227994e-03])

Lagrangian lambda: Vector(48, [-2.734832e-01, -2.357151e-01, -5.600838e+00, 4.680298e+00, 2.869063e+00, 3.429333e+00, -1.051514e+01, 4.019474e+00, 4.562744e+00, -3.844391e+00, 6.076568e-01, 1.240778e+00, -2.598041e+00, 2.869063e+00, 4.562744e+00, 3.844391e+00, -2.734832e-01, -2.357151e-01, -5.600838e+00, 4.680298e+00, 3.429333e+00, 1.051514e+01, 6.076568e-01, 1.240778e+00, -2.598041e+00, 7.424326e-01, 1.500453e+00, -5.473639e-01, 3.799861e-01, 8.552143e-01, 1.388457e-01, -9.732751e-01, 3.792795e-01, 4.434887e-01, 1.061503e+00, 8.386399e-01, -7.359292e-01, 7.424326e-01, 1.500453e+00, -5.473639e-01, 8.552143e-01, 8.386399e-01, 7.359292e-01, 3.799861e-01, 3.792795e-01, 4.434887e-01, 1.388457e-01, 9.732751e-01])

Matlab plot of the solution: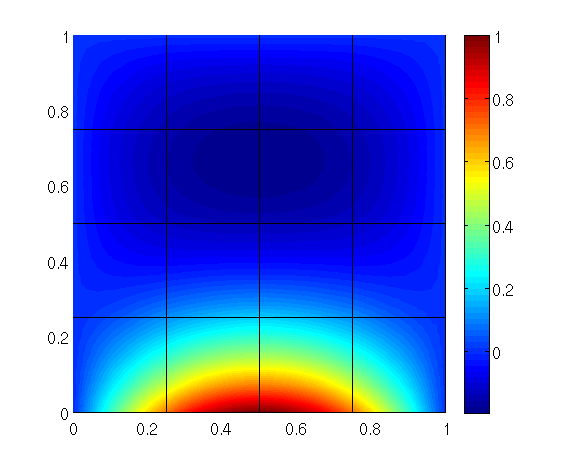

@section complete Complete Source Code
@author Dirk Klindworth, 2012

#include <iostream>
 
#include "basics.hh"
#include "formula.hh"
#include "function.hh"
#include "geometry.hh"
#include "graphics.hh"
#include "hp1D.hh"
#include "hp2D.hh"
#include "operator.hh"
#include "space.hh"
#include "toolbox.hh"
 
using concepts::Real;
 
int main(int argc, char** argv) {
  try {
 
#ifdef HAS_MPI
    // Initialisation is necessary if parallel version of Mumps is compiled
    MPI_Init(&argc, &argv);
#endif
 
    concepts::Import2dMesh msh(SOURCEDIR "/applications/unitsquareCoordinates.dat",
                               SOURCEDIR "/applications/unitsquareElements.dat",
                               SOURCEDIR "/applications/unitsquareEdges.dat");
    std::cout << std::endl << "Mesh: " << msh << std::endl;
    graphics::drawMeshEPS(msh, "mesh.eps",100,1.0,1);
 
    // ** write attributes of boundary edges to a set **
    concepts::Set<uint> attrBoundaryEdges;
    for (uint i = 1; i <= 4; ++i)
      attrBoundaryEdges.insert(i);
    
    // ** space **
    hp2D::hpAdaptiveSpaceH1 spc(msh, 2, 3);
    spc.rebuild();
    std::cout << std::endl << "Space:" << std::endl << spc << std::endl;
    graphics::drawMeshEPS(spc, "space.eps",100,1.0,1);
    
    // ** trace space and its dual space **
    hp2D::TraceSpace tspc(spc, attrBoundaryEdges);
    std::cout << std::endl << "Trace Space:" << std::endl << tspc << std::endl;
    hp1D::DualSpace dspc(tspc.scan());
    std::cout << std::endl << "Dual Space:" << std::endl << dspc << std::endl;
    
    // ** right hand side block vectors **
    hp2D::Riesz<Real> lform2D(concepts::ParsedFormula<>("(-5*exp(-(x-0.5)*(x-0.5)-(y-0.5)*(y-0.5)))"));
    concepts::Vector<Real> rhs2D(spc, lform2D);
    std::cout << std::endl << "RHS Vector 2D:" << std::endl << rhs2D << std::endl;
    hp1D::Riesz<Real> lform1D(concepts::ParsedFormula<>("(sin(pi*x)*cos(pi/2*y))"));
    concepts::Vector<Real> rhs1D(dspc,lform1D);    
    std::cout << std::endl << "RHS Vector 1D:" << std::endl << rhs1D << std::endl;
    concepts::Vector<Real> rhs(spc.dim()+dspc.dim());
    for (uint i=0; i<spc.dim(); i++)
      rhs(i)           = rhs2D(i);
    for (uint i=0; i<dspc.dim(); i++)
      rhs(spc.dim()+i) = rhs1D(i);
    std::cout << std::endl << "RHS Vector:" << std::endl << rhs << std::endl;
    
    // ** left hand side block matrices **
    hp2D::Laplace<Real> la;
    concepts::SparseMatrix<Real> A11(spc, la);
    A11.compress();
    std::cout << std::endl << "System Matrix A11:" << std::endl << A11 << std::endl;
    hp2D::Identity<Real> id;
    concepts::SparseMatrix<Real> M11(spc, id);
    M11.compress();
    std::cout << std::endl << "System Matrix M11:" << std::endl << M11 << std::endl;
    hp1D::Identity<Real> id1D;
    concepts::SparseMatrix<Real> M12(tspc,dspc,id1D);
    M12.compress();
    std::cout << std::endl << "System Matrix M12:" << std::endl << M12 << std::endl;
    concepts::SparseMatrix<Real> M21(dspc,tspc,id1D);
    M21.compress();
    std::cout << std::endl << "System Matrix M21:" << std::endl << M21 << std::endl;
    concepts::SparseMatrix<Real> A(spc.dim()+dspc.dim(),spc.dim()+dspc.dim());
    A11.addInto(A,  1.0,         0,         0);
    M11.addInto(A,  1.0,         0,         0);
    M12.addInto(A, -1.0,         0, spc.dim());
    M21.addInto(A,  1.0, spc.dim(),         0);
    std::cout << std::endl << "System Matrix A:" << std::endl << A << std::endl;
    
    // ** solve **
#ifdef HAS_MUMPS
    concepts::Mumps<Real> solver(A);
#else
    concepts::SuperLU<Real> solver(A);
#endif
    concepts::Vector<Real> sol(spc.dim()+dspc.dim());
    solver(rhs, sol);
    std::cout << std::endl << "Solver:" << std::endl << solver << std::endl;
    
    // ** read solution u and Lagrangian lambda from solution vector sol **
    concepts::Vector<Real> u(spc.dim());
    concepts::Vector<Real> lambda(dspc.dim());
    for (uint i=0; i<spc.dim(); i++)
      u(i)      = sol(i);
    std::cout << std::endl << "Solution u:" << std::endl << u << std::endl;
    for (uint i=0; i<dspc.dim(); i++)
      lambda(i) = sol(spc.dim()+i);
    std::cout << std::endl << "Lagrangian lambda:" << std::endl << lambda << std::endl;
            
    // ** plot solution **  
    hp2D::IntegrableQuad::factory().get()->setTensor(concepts::TRAPEZE, true, 8);
    spc.recomputeShapefunctions();
    graphics::MatlabGraphics(spc, "inhomDirichletLagrange", u);
  }
  catch (concepts::ExceptionBase& e) {
    std::cout << e << std::endl;
    return 1;
  }
#ifdef HAS_MPI
  MPI_Finalize();
#endif
 
  return 0;
}