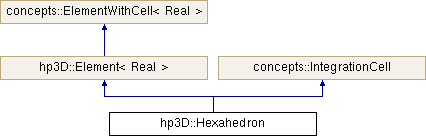
hp3D::Hexahedron Class Referenceabstract
A 3D FEM element: a hexahedron. More...
#include <hexahedron.hh>
Public Types | |
| enum | intFormType { ZERO, ONE, TWO, THREE } |
| Integration form, which determines terms coming from integration over reference element. More... | |
| typedef Real | type |
Public Member Functions | |
| void | appendT (concepts::TColumn< Real > *T) |
| Appends the T columns to the T matrix. More... | |
| virtual const concepts::Hexahedron3d & | cell () const |
| virtual const concepts::Cell3 & | cell () const=0 |
| Returns the cell on which the element is built. More... | |
| concepts::Real3d | chi (const Real x, const Real y, const Real z) const |
| Computes the element map. More... | |
| const concepts::AdaptiveControlP< 1 > & | edgeP (const uint i) const |
Get polynomial degree of edge i. More... | |
| void | edgeP (const uint i, const concepts::AdaptiveControlP< 1 > &p) |
Set polynomial degree of edge i to p. More... | |
| Real3d | elemMap (const Real coord_local) const |
| Real3d | elemMap (const Real2d &coord_local) const |
| Real3d | elemMap (const Real3d &coord_local) const |
| const concepts::AdaptiveControlP< 2 > & | faceP (const uint i) const |
Get polynomial degree of face i. More... | |
| void | faceP (const uint i, const concepts::AdaptiveControlP< 2 > &p) |
Set polynomial degree of face i to p. More... | |
| const concepts::Hex3dSubdivision * | getStrategy () const |
| Returns the subdivision strategy of the underlying cell of this element. More... | |
| virtual const concepts::ElementGraphics< Real > * | graphics () const |
| bool | hasSameMatrix (const Hexahedron &elm) const |
| Returns true if element matrix is the same. More... | |
| concepts::MapReal3d | hessian (const uint i, const Real x, const Real y, const Real z) const |
| Computes the Hessian. More... | |
| Hexahedron (concepts::Hexahedron3d &cell, const ushort *p, concepts::TColumn< Real > *T0, concepts::TColumn< Real > *T1) | |
| Constructor. More... | |
| const concepts::QuadratureRule1d * | integrationX () const |
| Returns the integration rule in x direction. More... | |
| const concepts::QuadratureRule1d * | integrationY () const |
| Returns the integration rule in y direction. More... | |
| const concepts::QuadratureRule1d * | integrationZ () const |
| Returns the integration rule in z direction. More... | |
| concepts::MapReal3d | jacobian (const Real x, const Real y, const Real z) const |
| Computes the Jacobian. More... | |
| Real | jacobianDeterminant (const Real x, const Real y, const Real z) const |
| Computes the determinant of the Jacobian. More... | |
| concepts::MapReal3d | jacobianInverse (const Real x, const Real y, const Real z) const |
| Computes the inverse of the Jacobian. More... | |
| virtual bool | operator< (const Element< Real > &elm) const |
| Comparison operator for elements. More... | |
| const ushort * | p () const |
| Returns the polynomial degree. More... | |
| virtual bool | quadraturePoint (uint i, intPoint &p, intFormType form, bool localCoord) const |
| Delivers a quadrature point. More... | |
| void | recomputeShapefunctions () |
| void | recomputeShapefunctions (const uint nq[2]) |
| void | setStrategy (const concepts::Hex3dSubdivision *strategy=0) throw (concepts::StrategyChange) |
| Sets the subdivision strategy of the underlying cell of this element. More... | |
| const concepts::Karniadakis< 1, 1 > * | shpfctDX () const |
| Returns the derivatives of the shape functions in x direction. More... | |
| const concepts::Karniadakis< 1, 1 > * | shpfctDY () const |
| Returns the shape functions in y direction. More... | |
| const concepts::Karniadakis< 1, 1 > * | shpfctDZ () const |
| Returns the shape functions in z direction. More... | |
| const concepts::Karniadakis< 1, 0 > * | shpfctX () const |
| Returns the shape functions in x direction. More... | |
| const concepts::Karniadakis< 1, 0 > * | shpfctY () const |
| Returns the shape functions in y direction. More... | |
| const concepts::Karniadakis< 1, 0 > * | shpfctZ () const |
| Returns the shape functions in z direction. More... | |
| virtual const concepts::Hexahedron & | support () const |
| virtual const concepts::Connector3 & | support () const=0 |
| Returns the topolgical support of the element. More... | |
| virtual const concepts::TMatrix< Real > & | T () const |
| Returns the T matrix of the element. More... | |
| virtual concepts::Real3d | vertex (uint i) const |
| Returns the coordinates of the ith vertex of this element. More... | |
| virtual | ~Hexahedron () |
Static Public Member Functions | |
| static concepts::QuadRuleFactory & | rule () |
| Access to the quadrature rule, which is valid for all elements of this type (hp3D::Hexaedron). More... | |
Protected Member Functions | |
| void | computeShapefunctions_ (const concepts::QuadratureRule1d *intX, const concepts::QuadratureRule1d *intY, const concepts::QuadratureRule1d *intZ) |
| gets the shapefunctions, used in both constructors More... | |
| virtual std::ostream & | info (std::ostream &os) const |
Protected Attributes | |
| concepts::TMatrix< Real > | T_ |
| T matrix of the element. More... | |
Private Attributes | |
| concepts::Hexahedron3d & | cell_ |
| The cell. More... | |
| const concepts::AdaptiveControlP< 1 > * | edges_ [12] |
| Polynomial degree of edges. More... | |
| const concepts::AdaptiveControlP< 2 > * | faces_ [6] |
| Polynomial degree of faces. More... | |
| std::unique_ptr< concepts::QuadratureRule1d > | intX_ |
| The integration rules. More... | |
| std::unique_ptr< concepts::QuadratureRule1d > | intY_ |
| std::unique_ptr< concepts::QuadratureRule1d > | intZ_ |
| ushort | p_ [3] |
| Polynomial degree. More... | |
| std::unique_ptr< concepts::Karniadakis< 1, 1 > > | shpfctDX_ |
| The derivatives of the shape functions. More... | |
| std::unique_ptr< concepts::Karniadakis< 1, 1 > > | shpfctDY_ |
| std::unique_ptr< concepts::Karniadakis< 1, 1 > > | shpfctDZ_ |
| std::unique_ptr< concepts::Karniadakis< 1, 0 > > | shpfctX_ |
| The shape functions. More... | |
| std::unique_ptr< concepts::Karniadakis< 1, 0 > > | shpfctY_ |
| std::unique_ptr< concepts::Karniadakis< 1, 0 > > | shpfctZ_ |
Static Private Attributes | |
| static std::unique_ptr< HexahedronGraphics > | graphics_ |
| static concepts::QuadRuleFactory | rule_ |
Detailed Description
A 3D FEM element: a hexahedron.
- Todo:
- remove this statement
Definition at line 37 of file hexahedron.hh.
Member Typedef Documentation
◆ type
|
inherited |
Definition at line 81 of file element.hh.
Member Enumeration Documentation
◆ intFormType
|
inherited |
Integration form, which determines terms coming from integration over reference element.
| Enumerator | |
|---|---|
| ZERO | |
| ONE | |
| TWO | |
| THREE | |
Definition at line 29 of file integral.hh.
Constructor & Destructor Documentation
◆ Hexahedron()
| hp3D::Hexahedron::Hexahedron | ( | concepts::Hexahedron3d & | cell, |
| const ushort * | p, | ||
| concepts::TColumn< Real > * | T0, | ||
| concepts::TColumn< Real > * | T1 | ||
| ) |
Constructor.
- Parameters
-
cell Cell on which the element is defined p Polynomial degree (can be anisotropic), this array must have at least 3 entries. T0 Part of the T matrix T1 Part of the T matrix
◆ ~Hexahedron()
|
virtual |
Member Function Documentation
◆ appendT()
|
inlineinherited |
Appends the T columns to the T matrix.
Definition at line 62 of file element.hh.
◆ cell() [1/2]
|
inlinevirtual |
Definition at line 56 of file hexahedron.hh.
◆ cell() [2/2]
|
pure virtualinherited |
Returns the cell on which the element is built.
Possible are tetrahedrons, hexahedron, prims and pyramids.
Implements concepts::ElementWithCell< Real >.
◆ chi()
|
inline |
Computes the element map.
The reference element is the unit cube.
Definition at line 101 of file hexahedron.hh.
◆ computeShapefunctions_()
|
protected |
gets the shapefunctions, used in both constructors
◆ edgeP() [1/2]
|
inline |
Get polynomial degree of edge i.
Definition at line 169 of file hexahedron.hh.
◆ edgeP() [2/2]
|
inline |
Set polynomial degree of edge i to p.
Definition at line 164 of file hexahedron.hh.
◆ elemMap() [1/3]
|
inlineinherited |
Definition at line 86 of file element.hh.
◆ elemMap() [2/3]
|
inlineinherited |
Definition at line 90 of file element.hh.
◆ elemMap() [3/3]
|
inlineinherited |
Definition at line 94 of file element.hh.
◆ faceP() [1/2]
|
inline |
Get polynomial degree of face i.
Definition at line 180 of file hexahedron.hh.
◆ faceP() [2/2]
|
inline |
Set polynomial degree of face i to p.
Definition at line 175 of file hexahedron.hh.
◆ getStrategy()
|
inline |
Returns the subdivision strategy of the underlying cell of this element.
Definition at line 148 of file hexahedron.hh.
◆ graphics()
|
virtual |
◆ hasSameMatrix()
| bool hp3D::Hexahedron::hasSameMatrix | ( | const Hexahedron & | elm | ) | const |
Returns true if element matrix is the same.
This method returns true if the element matrix of this element and elm are the same. To find this out, the length of the edges and their angles and the polynomial degrees are compared.
◆ hessian()
|
inline |
Computes the Hessian.
Definition at line 126 of file hexahedron.hh.
◆ info()
|
protectedvirtual |
Reimplemented from hp3D::Element< Real >.
◆ integrationX()
|
inline |
Returns the integration rule in x direction.
Definition at line 87 of file hexahedron.hh.
◆ integrationY()
|
inline |
Returns the integration rule in y direction.
Definition at line 91 of file hexahedron.hh.
◆ integrationZ()
|
inline |
Returns the integration rule in z direction.
Definition at line 95 of file hexahedron.hh.
◆ jacobian()
|
inline |
Computes the Jacobian.
Definition at line 107 of file hexahedron.hh.
◆ jacobianDeterminant()
|
inline |
Computes the determinant of the Jacobian.
Definition at line 121 of file hexahedron.hh.
◆ jacobianInverse()
|
inline |
Computes the inverse of the Jacobian.
Definition at line 115 of file hexahedron.hh.
◆ operator<()
|
virtual |
Comparison operator for elements.
Implements hp3D::Element< Real >.
◆ p()
|
inlineinherited |
Returns the polynomial degree.
The returned array has 3 elements.
Definition at line 51 of file element.hh.
◆ quadraturePoint()
|
virtual |
Delivers a quadrature point.
Quadrature point consists of coordinates (for evaluation of formulas) and intermediate data, consisting of the weight and term coming from mapping.
Returns false, if the number of quadrature points is overstepped.
- Parameters
-
i number of quadrature point intPoint data given back form Integration form localCoord If true, local coordinates are returned. Else physical coordinates.
Implements concepts::IntegrationCell.
◆ recomputeShapefunctions() [1/2]
| void hp3D::Hexahedron::recomputeShapefunctions | ( | ) |
◆ recomputeShapefunctions() [2/2]
| void hp3D::Hexahedron::recomputeShapefunctions | ( | const uint | nq[2] | ) |
◆ rule()
|
inlinestatic |
Access to the quadrature rule, which is valid for all elements of this type (hp3D::Hexaedron).
Change of the quadrature rule is put into practice for newly created elements and for already created elements by precomputing the integration points and shape functions on them.
Definition at line 193 of file hexahedron.hh.
◆ setStrategy()
|
inline | ||||||||||||||
Sets the subdivision strategy of the underlying cell of this element.
It calls Quad2d::setStrategy.
- Parameters
-
strategy Pointer to an instance of a subdivision strategy.
- Exceptions
-
StrategyChange if the change is not allowed (the change is not allowed if there are children present)
Definition at line 140 of file hexahedron.hh.
◆ shpfctDX()
|
inline |
Returns the derivatives of the shape functions in x direction.
Definition at line 74 of file hexahedron.hh.
◆ shpfctDY()
|
inline |
Returns the shape functions in y direction.
Definition at line 78 of file hexahedron.hh.
◆ shpfctDZ()
|
inline |
Returns the shape functions in z direction.
Definition at line 82 of file hexahedron.hh.
◆ shpfctX()
|
inline |
Returns the shape functions in x direction.
Definition at line 61 of file hexahedron.hh.
◆ shpfctY()
|
inline |
Returns the shape functions in y direction.
Definition at line 65 of file hexahedron.hh.
◆ shpfctZ()
|
inline |
Returns the shape functions in z direction.
Definition at line 69 of file hexahedron.hh.
◆ support() [1/2]
|
inlinevirtual |
Definition at line 50 of file hexahedron.hh.
◆ support() [2/2]
|
pure virtualinherited |
Returns the topolgical support of the element.
Possible supports for an element are hexahedrons, tetrahedrons, prisms and pyramids.
◆ T()
|
inlinevirtualinherited |
Returns the T matrix of the element.
Implements concepts::ElementWithCell< Real >.
Definition at line 59 of file element.hh.
◆ vertex()
|
inlinevirtual |
Returns the coordinates of the ith vertex of this element.
- Parameters
-
i Index of the vertex
Implements hp3D::Element< Real >.
Definition at line 53 of file hexahedron.hh.
Member Data Documentation
◆ cell_
|
private |
The cell.
Definition at line 210 of file hexahedron.hh.
◆ edges_
|
private |
Polynomial degree of edges.
Definition at line 219 of file hexahedron.hh.
◆ faces_
|
private |
Polynomial degree of faces.
Definition at line 221 of file hexahedron.hh.
◆ graphics_
|
staticprivate |
Definition at line 223 of file hexahedron.hh.
◆ intX_
|
private |
The integration rules.
Definition at line 216 of file hexahedron.hh.
◆ intY_
|
private |
Definition at line 216 of file hexahedron.hh.
◆ intZ_
|
private |
Definition at line 216 of file hexahedron.hh.
◆ p_
|
private |
Polynomial degree.
Definition at line 229 of file hexahedron.hh.
◆ rule_
|
staticprivate |
Definition at line 226 of file hexahedron.hh.
◆ shpfctDX_
|
private |
The derivatives of the shape functions.
Definition at line 214 of file hexahedron.hh.
◆ shpfctDY_
|
private |
Definition at line 214 of file hexahedron.hh.
◆ shpfctDZ_
|
private |
Definition at line 214 of file hexahedron.hh.
◆ shpfctX_
|
private |
The shape functions.
Definition at line 212 of file hexahedron.hh.
◆ shpfctY_
|
private |
Definition at line 212 of file hexahedron.hh.
◆ shpfctZ_
|
private |
Definition at line 212 of file hexahedron.hh.
◆ T_
|
protectedinherited |
T matrix of the element.
Definition at line 81 of file element.hh.
The documentation for this class was generated from the following file:
- hp3D/hexahedron.hh

