6 Analysis of categorical data

6.1 Theorie in Kürze * Fisher-Test: Zusammenhang zwischen zwei binären

Variablen (22 Tabelle); Verteilung der Teststatistik unter $H_0$: “Variablen sind unabhängig” ist auch für kleine Stichprobengrössen bekannt; die Stärke der Abhängigkeit zwischen den beiden Variablen wir mit dem odds-Ratio quantifiziert Chi-Quadrat Test: Zusammenhang zwischen zwei kategoriellen Variablen (mn Tabelle); Verteilung der Teststatistik unter $H_0$: “Variablen sind unabhängig” ist nur asymptotisch (also für grosse Stichprobengrössen) bekannt; daher ist Fisher-Test bei zweistufigen Faktoren besser geeignet, obwohl man auch einen Chi-Quadrat Test machen könnte. Es gibt keine einfache Zahl, die die Stärke der Abhängigkeit zwischen Zwei Faktoren mit mehr als zwei Stufen quantifizieren könnte. Teststatistik beim Chi-Quadrat Test: $\chi^2 = \sum_{i=1}^m \sum_{j=1}^n R_{ij}^2$. Dabei sind $R_{ij} = \frac{O_{ij} - E_{ij}}{\sqrt{E_{ij}}}$ die Pearson Residuen, die den Unterschied zwischen beobachteten Tabellenwerten $O_{ij}$ und unter der $H_0$ erwarteten Tabellenwerten $E_{ij}$ quantifizieren. Unter der $H_0$ folgt $\chi^2$ einer Chi-Quadrat Verteilung mit $(n-1)*(m-1)$ Freiheitsgraden. Unter $H_0$ gilt $E_{ij} = \frac{N_{\cdot i}N_{j\cdot}}{N}$.

Wichtige R Funktionen: , , ; aus dem Paket

6.2 Bsp: Fisher Test

Angenommen 45 Patienten wurden in zwei Gruppen randomisiert: 25 in die Medikamenten-Gruppe, 20 in die Placebo-Gruppe. In der Medikamenten-Gruppe wurde 15 Patienten geheilt und 10 nicht geheilt. In der Placebo-Gruppe wurden 9 Patienten geheilt und 11 nicht geheilt. Angenommen, das Medikament wirkt gar nicht (also ist Medikamenten-Abgabe und Heilung unabhängig). Ist dann die gemachte Beobachtung unplausibel oder relativ normal ?

m <- matrix(c(15,10, 9,11), 2,2)
fisher.test(m, alternative = "greater")

## 
##  Fisher's Exact Test for Count Data
## 
## data:  m
## p-value = 0.2416
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
##  0.5753718       Inf
## sample estimates:
## odds ratio 
##   1.808415

Der p-Wert des Fisher-Tests ist $0.24$. D.h., unter der $H_0$ ist die gemachte Beobachtung nicht ungewöhnlich und wir können die Nullhypothese nicht verwerfen. Die odds werden zu $1.81$ geschätzt mit einem 95%-VI von $[0.575, \infty]$ (wir haben einen einseitigen Test gemacht, daher ist eine Grenze des VIs unendlich, also $\infty$).

6.3 Bsp: Chi-Quadrat Test

Gibt es einen Zusammenhang zwischen Augen- und Haarfarbe? Folgende Daten stehen zur Verfügung (also z.B. 68 Personen mit schwarzen Haaren und braunen Augen):

## table to df: as.data.frame
df <- as.data.frame(HairEyeColor)
tab <- xtabs(Freq ~ Hair + Eye, data = df)
tab

##        Eye
## Hair    Brown Blue Hazel Green
##   Black    68   20    15     5
##   Brown   119   84    54    29
##   Red      26   17    14    14
##   Blond     7   94    10    16

Wir untersuchen den Zusammenhang mit einem Chi-Quadrat Test:

res <- chisq.test(tab)
res

## 
##  Pearson's Chi-squared test
## 
## data:  tab
## X-squared = 138.29, df = 9, p-value < 2.2e-16

Die Nullhypothese “Augen- und Haarfarbe” sind unabhängig kann klar verworfen werden. Es scheint also einen Zusammenhand zwischen Augen- und Haarfarbe zu geben. Leider lässt sich nicht so einfach quantifizieren wo diese Zusammenhänge sind (z.B. könnte man vermuten, dass Personen mit blonden Haaren eher blaue Augen haben).

Um hier einen Schritt weiter zu kommen, schauen wir uns die Test-Statistik etwas genauer an. Sie besteht aus einer Summe von quadrierten Pearson-Residuen und dabei gibt es pro Tabellen-Feld genau ein Pearson-Residuum. Wenn die Test-Statistik (Summe) auffallend gross ist (in unserem Fall $138.29$), gibt es wahrscheinlich einen oder mehrere Summanden (Person-Residuen in gewissen Tabellenfeldern), die auffallend gross sind. Die Pearson-Residuen sind im Testobjekt gespeichert.

res$residuals

##        Eye
## Hair          Brown        Blue       Hazel       Green
##   Black  4.39839852 -3.06937747 -0.47735203 -1.95368354
##   Brown  1.23345810 -1.94947682  1.35328398 -0.34509961
##   Red   -0.07497794 -1.73012546  0.85225273  2.28273672
##   Blond -5.85099741  7.04959022 -2.22784430  0.61269815

Z.B. für das Tabellen-Feld bei blauen Augen und blonden Haaren (Zeile 4, Spalte 2) haben wir sehr grosse Pearson-Residuen (ca. $7$), hier gibt es also eine beträchtliche Diskrepanz zwischen beobachtetem Wert ($O_{4,2} = 94$) und unter der Nullhypothese erwartetem Wert ($E_{4,2} = 215*127/592 = 46.123$; da es sich hier um einen Erwartungswert handelt, kann eine Zahl rauskommen, die keine ganze Zahl ist). Mit $O_{4,2}$ und $E_{4,2}$ lässt sich dann mit der Formel $R_{ij} = \frac{O_{ij} - E_{ij}}{\sqrt{E_{ij}}}$ der Wert des Pearson-Residuums für die Zeile 4 und Spalte 2 auch von Hand berechnen. Wie oben gezeigt, wurde dieser Wert aber schon beim Durchführen des Chi-Quadrat Tests berechnet und ist unter “$residuals$” für alle Tabellenfelder abrufbar. Übrigens sind auch die erwarteten Tabelleneinträge $E_{ij}$ alle schon berechnet unter res$expected.

Durch Analyse der Pearson-Residuen können wir also herausfinden, auf Grund welcher Tabellenfelder die Teststatistik so gross wurde, dass die Nullhypothese verworfen wird. Besonders komfortabel geht das grafisch mit dem Mosaicplot. Alle Tabellenfelder, deren Pearson-Residuen betragsmässig grösser als 2 sind, werden eingefärbt (je nach Vorzeichen rot oder blau; die Einfärbung hat dabei nichts damit zu tun, ob der entsprechende Chi-Quadrat Test signifikant ist):

library(vcd)

## Loading required package: grid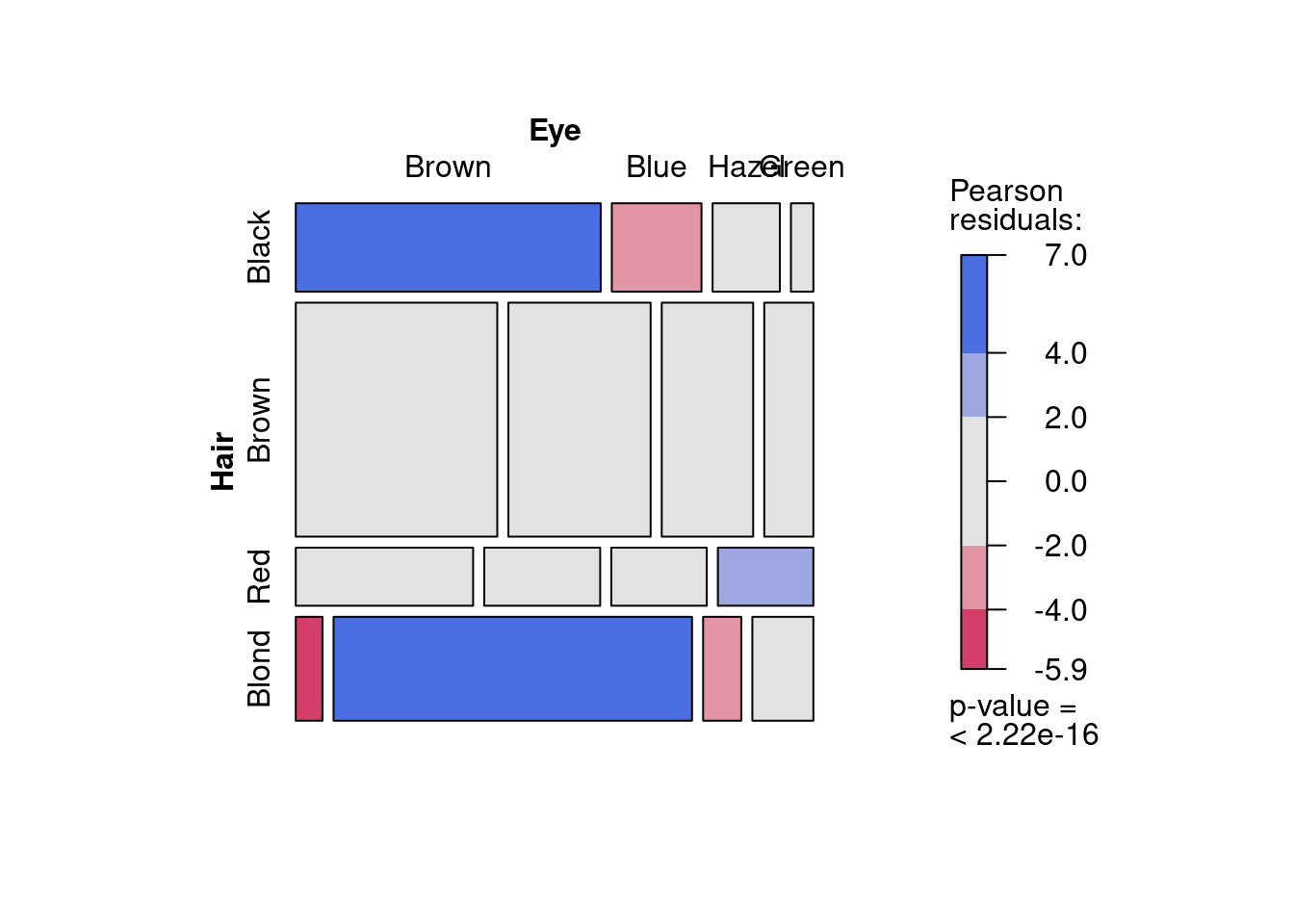

mosaic(Freq ~ Hair + Eye, data = df, shade = TRUE)

Zur Interpretation betrachten wir zunächst die Zeilen: Die “Dicke” jeder Zeile ist proportional zur Häufigkeit der entsprechenden Haarfarbe. Z.B. ist die Zeile “Brown” am dicksten, d.h., es gibt am meisten Braunhaarige. Zudem können wir mit dem Lineal ausmessen, dass die Zeile “Brown” ca. 2.5 mal so dick ist wie die Zeile “Black”. Das Verhältnis der Dicke entspricht in der Tat dem Verhältnis der Braunhaarigen (286) und Schwarzhaarigen (108). Anschliessend interpretieren wir die Spalten jeder Zeile. Sehen wir uns die Zeile “Blond” genauer an. Auf meinem Bildschirm messe ich mit dem Lineal folgende Breiten für die Kacheln zu “Brown”, “Blue”, “Hazel” und “Green”: 3mm, 40mm, 4mm, 7mm. D.h., die Anteile an der gesamten Kachelbreite (Summe aller Kachelbreiten ist 54mm) ist ca. 0.06, 0.74, 0.07, 0.13. Genau dieselben Anteile erhalten wir, wenn wir ausrechnen, wie viele Leute mit braunen, blauen, haselnussfarbigen und grünen Augen es unter den Blondhaarigen gibt. Der Mosaikplot zeigt also die Verteilung der Augenfarbe gegeben die entsprechende Zeile (zum Vergleich: Wenn wir nicht nur Blondhaarige sondern alle Personen berücksichtigen, sind die Anteile der Augenfarben anders, nämlich ca.: 0.37, 0.36, 0.16, 0.11). Wir sehen also, dass es bei den Blondhaarigen auffallend wenige Braunäugige und auffallend viele Blauäugige gibt. Entsprechend sind die Pearson-Residuen im Feld “blonde Haare, braune Augen” stark negativ (-5.8) und im Feld “blonde Haare, blaue Augen” stark positiv (7.0). Das Mosaik wird gemäss der Pearson-Residuen eingefärbt (rot für negative und blau für positive Residuen; eine Kachel wird nur dann eingefärbt, wenn das entsprechende Pearson Residuum vom Betrag her grösser als 2 ist). Schliesslich wird mit jedem Mosaikplot auch gleich ein Chi-Quadrat-Test durchgeführt. Der p-Wert erscheint rechts unten neben dem Plot und ist identisch mit der Ausgabe von .