2 Lineare Regression

2.1 Theorie in Kürze

Idee: Kontinuierliche Zielgrösse (\(Y\)) wird durch erklärende Variablen (\(X\), diese können kontinuierlich oder diskret, also Faktoren, sein) modelliert.
Modell: \[ Y_i = \beta_0 + \sum_{j=1}^{p-1} \beta_j x_{i,j} + E_i, \quad E_i \sim N(0,\sigma^2), \,\textrm{i.i.d.} \]
Einfache lineare Regression: Eine erklärende Variable
Multiple lineare Regression: Mehrere erklärende Variablen; Parameterwerte zur gleichen erklärenden Variable sind in einer einfachen und multiplen Regression üblicherweise unterschiedlich!
Tests:
- Für jeden Parameter \(\beta_j\) gibt es im summary-output einen \(t\)-Test mit \(H_0: \beta_j = 0\).
- Zudem testet der \(F\)-Test die Nullhypothese \(H_0: \beta_1 = \beta_2 = \ldots = \beta_{p-1} = 0\) (also alle \(\beta\)’s ausser Intercept); falls die erklärenden Variablen stark korreliert sind (“Kollinearität”) kann es vorkommen, dass der \(F\)-Test verworfen wird aber kein \(t\)-Test verworfen werden kann.
Vorhersage gegeben neue Werte der beobachteten Daten:
- Vertrauensintervall: für Erwartungswert \(E(Y)\)
- Vorhersageintervall: für einzelne neue Beobachtung \(Y\); das Vorhersageintervall ist grösser als das Vertrauensintervall.
Residuenanalyse:
- QQ-Plot Residuen um grobe Abweichungen der Normalverteilung der Fehler zu erkennen
- Tukey-Anscombe Plot um Fehler in der Modellform (z.B. fehlender quadratischer Term) oder schwankende Fehlervarianz zu erkennen
- Falls Residuenanalyse Probleme anzeigt: Transformationen von \(Y\) oder \(X\) (z.B. \(\log\) oder Wurzel); Achtung mit der Interpretation der Parameter nach einer Transformation.
Wichtige R-Funktionen: lm, summary, predict, plot, confint

2.2 Bsp 1: Spendengelder - Einfache Regression

Bei 100 Personen wurde erfasst, wie viel Geld (SFr) jede Person an eine bestimmte wohltätige Organistation in einem bestimmten Jahr gespendet hat. Pro Person ist sowohl Alter (kontinuierliche Variable) als auch Geschlecht (Faktorvariable) bekannt. Wie hängt der Spendenbetrag mit Alter und Geschlecht zusammen ?

load("spendengelder.rda")

Der dataframe dat enthält in der Spalte x das Alter (kontinuierlich), in der Spalte g das Geschlecht (Faktorvariable mit Levels M für männlich und W für weiblich; Referenzlevel ist M).

Mit einer einfachen linearen Regression könnten wir den Spendenbetrag nur durch das Alter erklären:

## Einfache lineare Regression: Spende vs. Alter
fmE1 <- lm(y ~ x, data = dat)
summary(fmE1)

## 
## Call:
## lm(formula = y ~ x, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -18.136  -9.379  -2.162  10.886  19.419 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -6.62180    3.05634  -2.167   0.0327 *  
## x            1.20838    0.05653  21.376   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.06 on 98 degrees of freedom
## Multiple R-squared:  0.8234, Adjusted R-squared:  0.8216 
## F-statistic: 456.9 on 1 and 98 DF,  p-value: < 2.2e-16

Der Intercept bezieht sich auf den erwarteten Spendenbetrag einer Person im Alter 0 (also bei der Geburt). In diesem Beispiel ist das sicher keine interessante Information. Die vom Modell vorhergesagte Zahl (\(-6.62\)) ist sogar negativ, also völlig unplausibel; wir könnten im Datensatz vom Alter eine Zahl, z.B. \(40\), abziehen. Diese neue Variable beschreibt dann für jede Person den Abstand vom Alter \(40\) und der Intercept bezieht sich auf den erwarteten Spendenbetrag im Alter 40 (also ist die Abweichung von \(40\) gleich \(0\)), was in diesem Beispiel sicher interessanter ist.

dat$x40 <- dat$x - 40
fmE2 <- lm(y ~ x40, data = dat)
summary(fmE2)

## 
## Call:
## lm(formula = y ~ x40, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -18.136  -9.379  -2.162  10.886  19.419 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 41.71344    1.25264   33.30   <2e-16 ***
## x40          1.20838    0.05653   21.38   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.06 on 98 degrees of freedom
## Multiple R-squared:  0.8234, Adjusted R-squared:  0.8216 
## F-statistic: 456.9 on 1 and 98 DF,  p-value: < 2.2e-16

Der erwartete Spendenbetrag einer vierzigjährigen Person ist also etwa \(41.7\) SFr. Das dazugehörige 95%-Vertrauensintervall erhalten wir mit

confint(fmE2, level = 0.95)

##                 2.5 %    97.5 %
## (Intercept) 39.227622 44.199265
## x40          1.096198  1.320564

was \([39.23, 44.20]\) liefert.

Nun zur Steigung: Wenn das Alter um ein Jahr zunimmt, sehen wir anhand obigen Outputs einen Anstieg des mittleren Spendenbetrags um ca. \(1.21\) SFr/Jahr (95%-Vertrauensintervall: \([1.10,1.32]\)).

Alternativ könnten wir den Spendenbetrag auch nur durch das Geschlecht erklären, was auch einer einfachen linearen Regression entspricht. Diesmal ist die erklärende Variable allerdings eine Faktorvariable und der Output wird deshalb etwas anders interpretiert:

## Einfache lineare Regression: Spende vs. Geschlecht
fmE3 <- lm(y ~ g, data = dat)
summary(fmE3)

## 
## Call:
## lm(formula = y ~ g, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -49.364 -14.802  -0.234  20.071  40.174 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   42.837      3.008  14.243  < 2e-16 ***
## gW            26.614      4.587   5.803 8.03e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 22.71 on 98 degrees of freedom
## Multiple R-squared:  0.2557, Adjusted R-squared:  0.2481 
## F-statistic: 33.67 on 1 and 98 DF,  p-value: 8.028e-08

confint(fmE3, level = 0.95)

##                2.5 %   97.5 %
## (Intercept) 36.86871 48.80572
## gW          17.51225 35.71602

Der Intercept bezieht sich nun auf das Referenzlevel des Faktors g (das ist das Level, das im Faktor in der Zeile Levels zuerst genannt wird), in diesem Fall die Männer (Level M). In der Zeile gW steht der Unterschied im erwarteten Spendenbetrag, wenn wir von der Referenzklasse der Männer in die Klasse der Frauen wechseln. Der erwartete Spendenbetrag ändert sich in diesem Fall um \(26.6\) (95%-Vertrauensintervall: \([17.5, 35.7]\)). Die Referenzklasse eines Faktors kann mit dem Befehl relevel geändert werden:

dat$g ## Referenzlevel 'M'

##   [1] W W M W M M W M M M W M W M W W W W M M M W M M W M M W M W W W M M M M W
##  [38] M M M M W W M W M M M W M M M W M M W M M M W W M M M W M W M W M M M W W
##  [75] M M W M M W M W W W W W W W W M W M M M M M M M W W
## Levels: M W

g2 <- relevel(dat$g, ref = 'W') ## Referenzlevel 'W'
g2

##   [1] W W M W M M W M M M W M W M W W W W M M M W M M W M M W M W W W M M M M W
##  [38] M M M M W W M W M M M W M M M W M M W M M M W W M M M W M W M W M M M W W
##  [75] M M W M M W M W W W W W W W W M W M M M M M M M W W
## Levels: W M

Der erwartete Spendenbetrag in der Gruppe der Männer ist also ca. \(42.8\) und der erwartete Spendenbetrag in der Gruppe der Frauen ist ca. \(42.8 + 26.6 = 69.4\).

Bemerkung: Für den erwarteten Spendenbetrag in der Gruppe der Männer und für die Differenz zwischen Männern und Frauen bekommen wir im summary-output Koeffizienten und Vertrauensintervalle. Das Vertrauensintervall für die Gruppe der Frauen bekommen wir mit obiger Auswertung leider nicht so einfach. Wir könnten das Referenzlevel zu W wechseln, dann steht der gewünschte Wert in der Zeile (Intercept) oder wir müssten mit Kontrasten rechnen, wie wir es später in der ANOVA machen werden.

2.3 Bsp 2: Spendengelder - Multiple Regression

In der multiplen Regression werden mehrere erklärende Variablen gleichzeitig verwendet. Die Koeffizienten können (müssen aber nicht) dabei komplett anders sein als in der einfachen Regression. Wir verwenden wieder die Altersdaten, die um das Alter \(40\) zentriert sind.

fmM1 <- lm(y ~ g + x40, data = dat)
summary(fmM1)

## 
## Call:
## lm(formula = y ~ g + x40, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.056  -3.170   0.242   2.555   9.565 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 33.59489    0.59916   56.07   <2e-16 ***
## gW          20.57122    0.87919   23.40   <2e-16 ***
## x40          1.13847    0.02225   51.18   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.313 on 97 degrees of freedom
## Multiple R-squared:  0.9734, Adjusted R-squared:  0.9729 
## F-statistic:  1776 on 2 and 97 DF,  p-value: < 2.2e-16

confint(fmM1, level = 0.95)

##                 2.5 %    97.5 %
## (Intercept) 32.405710 34.784061
## gW          18.826276 22.316169
## x40          1.094323  1.182626

Wie zu erwarten, sind die Parameter in der multiplen Regression anders als die Parameter in den entsprechenden einfachen Regressionen. Aus dem summary output können wir Folgendes ablesen: Männer im Alter von \(40\) haben einen erwarteten Spendenbetrag von ca. \(33.6\) SFr. Bei Frauen im gleichen Alter ist der erwartete Spendenbetrag um ca. \(20.6\) SFr grösser (im Alter \(40\) also etwa \(54.2\) SFr). Pro Jahr ändert sich der erwartete Spendenbetrag um ca. \(1.14\). D.h., eine Frau im Alter von \(45\) hätte gemässe diesem Modell einen erwarteten Spendenbetrag von ca. \(33.6 + 20.6 + 5 \cdot 1.14 \approx 59.9\) SFr.

Etwas einfacher (und gleich mit Vertrauens- bzw. Vorhersageintervall) geht so eine Vorhersage mit der Funktion predict:

## Vertrauensintervall für erwarteten Spendenbetrag
predict(fmM1, newdata = data.frame(x40 = 5, g = 'W'), 
        interval = "confidence", level = 0.95)

##        fit      lwr      upr
## 1 59.85848 58.50104 61.21593

## Vorhersageintervall für Spendenbetrag
predict(fmM1, newdata = data.frame(x40 = 5, g = 'W'), 
        interval = "prediction", level = 0.95)

##        fit      lwr      upr
## 1 59.85848 51.19098 68.52598

Die Funktion predict liefert praktisch das gleiche Ergebnis wie unsere Berechnung von Hand. Allerdings können wir nun auch ein 95%-Vertrauensintervall für den erwarteten Spendenbetrag oder ein 95%-Vorhersageintervall für den Spendenbetrag (Achtung: Ich habe das Wort “erwartet” absichtlich nicht verwendet) berechnen. Das 95%-Vertrauensintervall für den erwarteten Spendenbetrag ist ca. \([58.5; 61.2]\). D.h., wenn wir den mittleren Spendenbetrag einer grossen Gruppe von \(45\)-jährigen Frauen ausrechnen, wird diese Zahl wohl im Intervall \([58.5; 61.2]\) sein (mit 95% Wa.). Eine Frau im Alter von \(45\) Jahren kann natürlich einen ganz anderen Spendenbetrag haben. Der Spendenbetrag einer , zufällig ausgewählten Frau wird wohl im Intervall \([51.2; 68.5]\) sein (mit 95% Wa.). Das Vorhersageintervall ist typischerweise deutlich grösser als das Vertrauensintervall.

In obigem Modell erzwingen wir durch die Syntax g + x40 dieselbe Steigung bzgl. Alter bei Männern und Frauen. Mit der Syntax g * x40 kann das Modell unterschiedliche Steigungen für Männer und Frauen haben. Wir sprechen von einer Wechselwirkung (oder Interaktion) zwischen der Variable g und x40, weil der Zusammenhang von x40 und y davon abhängt, welchen Wert g gerade annimmt.

fmM2 <- lm(y ~ g * x40, data = dat)
summary(fmM2)

## 
## Call:
## lm(formula = y ~ g * x40, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -7.0026 -1.9035 -0.0448  1.5470  6.9818 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 34.85152    0.42283   82.42   <2e-16 ***
## gW          17.04550    0.68080   25.04   <2e-16 ***
## x40          0.98368    0.02088   47.11   <2e-16 ***
## gW:x40       0.32380    0.03020   10.72   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.925 on 96 degrees of freedom
## Multiple R-squared:  0.9879, Adjusted R-squared:  0.9875 
## F-statistic:  2614 on 3 and 96 DF,  p-value: < 2.2e-16

confint(fmM2, level = 0.95)

##                  2.5 %    97.5 %
## (Intercept) 34.0122027 35.690830
## gW          15.6941193 18.396887
## x40          0.9422385  1.025126
## gW:x40       0.2638579  0.383739

In der Zeile (Intercept) steht der Achsenabschnitt (hier also bei Alter \(40\) Jahre) der Referenzgruppe (also Männer). D.h., ein Mann im Alter von \(40\) Jahren hat gemäss diesem Modell einen erwarteten Spendenbetrag von ca. \(34.9\) SFr. Die Steigung bzgl. Alter für die Referenzgruppe steht in der Zeile x40: Wenn Männer ein Jahr älter werden, nimmt der erwartete Spendenbetrag um ca. \(0.98\) SFr zu. Um die entsprechenden Werte der Frauen abzulesen, muss man daran denken, dass im summary output Differenzen angegeben werden: Der Achsenabschnitt (also erwarteter Spendenbetrag im Alter \(40\) Jahre) bei Frauen ist um ca. \(17.0\) grösser als bei den Männern. D.h., die Frauen im Alter \(40\) haben einen erwarteten Spendenbetrag von ca. \(34.9 + 17.0 = 51.9\). Die Steigung bei den Frauen ist um ca. \(0.32\) grösser als bei den Männern. Die Steigung in der Gruppe der Frauen ist also ca. \(0.98 + 0.32 = 1.3\). Für Achsenabschnitt und Steigung in der Referenzgruppe und für die Unterschiede in Achsenabschnitt und Steigung können wir mit dem Befehl confint leicht Vertrauensintervalle berechnen. Für Achsenabschnitt und Steigung in der Gruppe der Frauen geht das nicht so einfach (siehe später das Thema “Kontraste” bei ANOVA).

Wir haben im Modell mit Wechselwirkung gesehen, dass der Wechselwirkungsterm hochsignifikant ist. Das kompliziertere Modell (vgl. mit dem Modell ohne Wechselwirkung) scheint als angebracht zu sein. Allgemein kann man geschachtelte Modelle (“nested models”; also bei denen man das einfachere Modell erhält, indem man im komplizierten Modell gewisse Parameter gleich null setzt) mit dem Befehl anova untersuchen um zu prüfen, ob das komplizierte Modell wirklich eine “signifikante” Verbesserung mit sich bringt. Hier am Beispiel der Modelle mit und ohne Wechselwirkung:

anova(fmM1, fmM2)

## Analysis of Variance Table
## 
## Model 1: y ~ g + x40
## Model 2: y ~ g * x40
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1     97 1804.57                                  
## 2     96  821.12  1    983.46 114.98 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Oben im Output werden zunächst die beiden Modelle, die untersucht werden, aufgeführt. Model 1 ist das Modell ohne Wechselwirkung, während Model 2 das Modell mit Wechselwirkung ist. Model 2 verwendet mehr Parameter, also würde man erwarten, dass es besser passt. In der Tat ist die Residual Sum of Squares (in der Spalte RSS) bei Model 1 \(1804.57\) und in Model 2 nur noch \(821.12\). Allerdings verwendet Model 2 auch einen Parameter mehr (Spalte Df). Nun wird ein Test gemacht mit der Nullhypothese, dass eben dieser zusätzliche Parameter in Wahrheit null ist (also eigentlich gar nicht gebraucht wird und das kleinere Modell somit ausreichend ist). Dazu wird ein \(F\)-Test gemacht (ähnlich wie der globale \(F\)-Test bei der Regression) und der p-Wert steht in der letzten Spalte (Pr(>F)). Wir sehen, dass in diesem Fall die Nullhypothese klar verworfen wird. D.h., es ist unplausibel, dass der zusätzliche Parameter null ist und somit sollten wir das kompliziertere Modell (mit Wechselwirkung) dem einfachen Modell (ohne Wechselwirkung) vorziehen. Mit dem gerade beschriebenen Vorgehen können beliebige geschachtelten Modelle in der Regression miteinander verglichen werden.

Abschliessend noch unsere Modelle mit und ohne Wechselwirkung in einem Plot. Ohne Wechselwirkung haben die Geraden in beiden Gruppen (Männer / Frauen) die gleiche Steigung, sind also parallel. Mit Wechselwirkung sind die Geraden nicht parallel.

mult.fig(mfrow= c(1,2))
x40new <- -30:40 ## Alter 10 bis 80
yM_noWW <- predict(fmM1, newdata = data.frame(x40 = x40new, g = 'M'))
yW_noWW <- predict(fmM1, newdata = data.frame(x40 = x40new, g = 'W'))
plot(x40new, yM_noWW, type = 'l', 
     ylim = c(0,100), xlab = "Alter - 40", ylab = "E[Spendenbetrag]",
     main = "Ohne WW")
points(x40new, yW_noWW, type = 'l', col = 2)

yM_WW <- predict(fmM2, newdata = data.frame(x40 = x40new, g = 'M'))
yW_WW <- predict(fmM2, newdata = data.frame(x40 = x40new, g = 'W'))
plot(x40new, yM_WW, type = 'l', 
     ylim = c(0,100), xlab = "Alter - 40", ylab = "E[Spendenbetrag]",
     main = "Mit WW")
points(x40new, yW_WW, type = 'l', col = 2)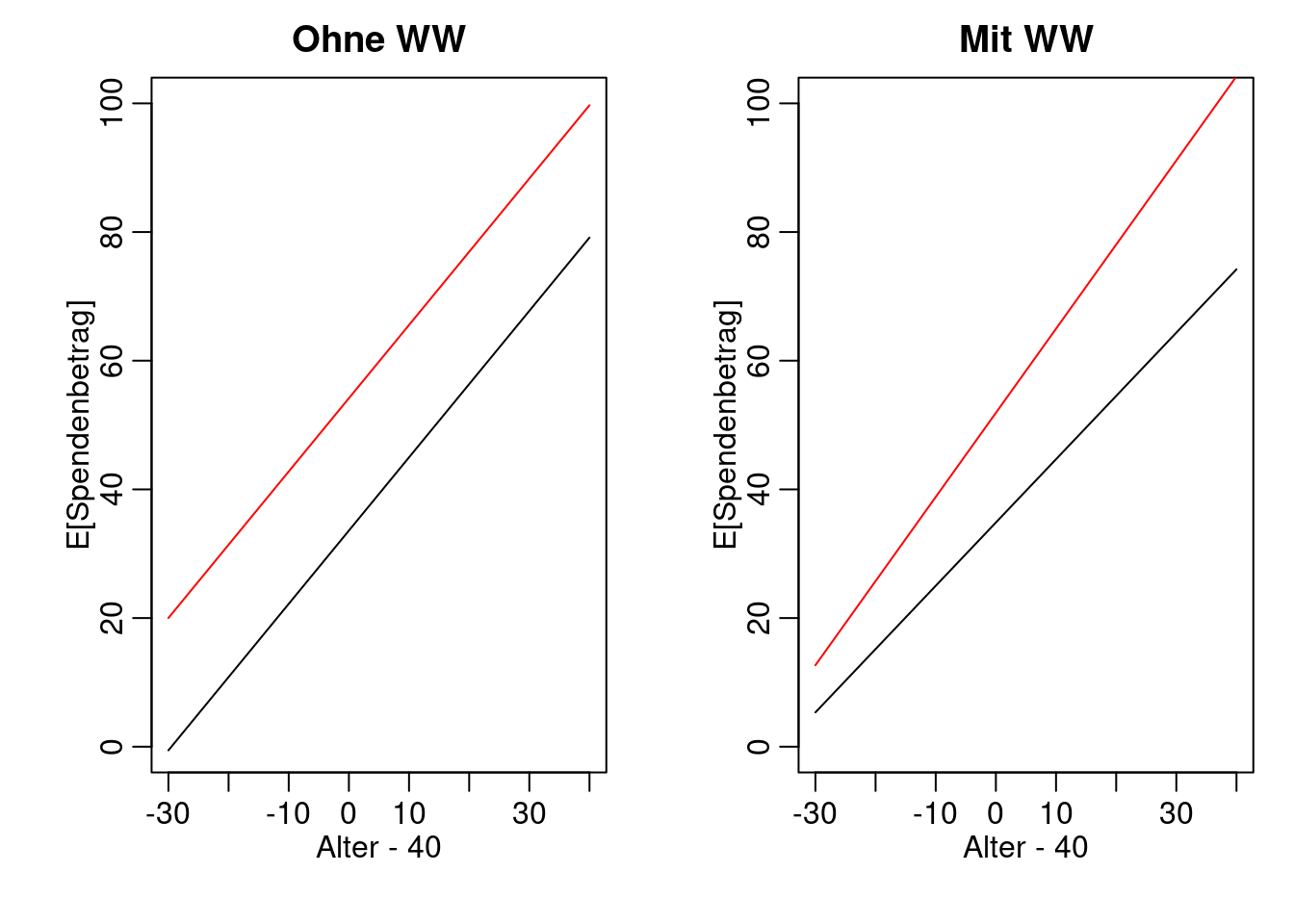

2.4 Bsp 3: Einfache vs. multiple Regression

Parameter, die in der multiplen linearen Regression geschätzt werden sind normalerweise ganz anders als die Parameter, die in den entsprechenden einfachen Regressionen geschätzt werden. Das tritt vor allem dann auf, wenn die erklärenden Variablen stark korreliert sind. Hier ein einfaches Beispiel (aus der Vorlesung “Regression”):

x1 <- c(0, 1, 2, 3, 0, 1, 1.9, 3)
x2 <- c(-1.1, 0.1, 1, 2.1, 1, 2, 3, 4)
y  <- c(1, 2, 3, 4, -1, 0, 1, 2)
cor(x1, x2)

## [1] 0.7495477

x1 und x2 sind korreliert; es ist also zu erwarten, dass die einfache und multiple Regression unterschiedliche Parameter schätzen werden:

coef(lm(y ~ x2)) ## Parameter bei x2 ist leicht positiv

## (Intercept)          x2 
##   1.3060765   0.1282139

coef(lm(y ~ x1 + x2)) ## Parameter bei x2 ist deutlich negativ

## (Intercept)          x1          x2 
## -0.01253648  2.01641749 -0.98306416

In der einfachen Regression ist der Parameter bei x2 leicht positiv. In der multiplen Regression ist der Parameter bei x2 allerdings deutlich negativ. Es gibt hier kein richtig oder falsch: Die einfache Regression modelliert den “marginalen” Zusammenhang; d.h., gemäss unserem Modell ändert sich y um \(0.13\), wenn sich x2 um eine Einheit erhöht (ohne Einschränkung an x1). Die multiple Regression modelliert den “bereinigten” Zusammenhang; d.h., gemäss unserem Modell ändert sich y um \(-1\), wenn sich x2 um eine Einheit erhöht .

In diesem einfachen Beispiel können wir das Verhalten verstehen: Die verwendeten Punkte stammen ziemlich genau von der Ebene \(y = 2 \cdot x_1 - x_2\) (Sie können z.B. Wolfram Alpha im Internet verwenden, um diese Ebene zu plotten: plot(y = 2x1 - x2); alternativ finden Sie unten einen auskommentierten R Code, mit dem Sie die Ebene und die Punkte mit einem interaktiven 3d-Plot darstellen können). Für jedes fixe \(x_1\) nimmt \(y\) in Richtung \(x_2\) ab. Wenn wir allerdings Punkte in dieser Ebene “geschickt” auswählen und dann die Information bzgl. \(x_1\) weglassen (d.h. die Punkte auf die Ebene \(x_2\)-\(y\) projizieren), können wir erreichen, dass in dem so gewählten Datensatz \(y\) in Richtung \(x_2\) zunimmt. Das ist die Sicht der einfachen Regression.

## evtl. müssen Sie zuerst 'install.packages("rgl")' ausführen
## library(rgl) 
## plot3d(x1,x2,y)
## planes3d(2, -1, -1, 0, alpha = 0.3)

mult.fig(mfrow = c(1, 2))
## Schnitt durch die Ebene bei x1 = 0 -> y = -x2
x2Tmp <- seq(-1, 4, by = 0.1)
yTmp <- -x2Tmp
plot(x2Tmp, yTmp, main = "x1=0 fix")
## Unsere ausgewählten Punkte, wenn man die x1-Koordinate weglässt
plot(x2, y, main = "marginal")
abline(lm(y ~ x2)) ## gefittete Regressionsgerade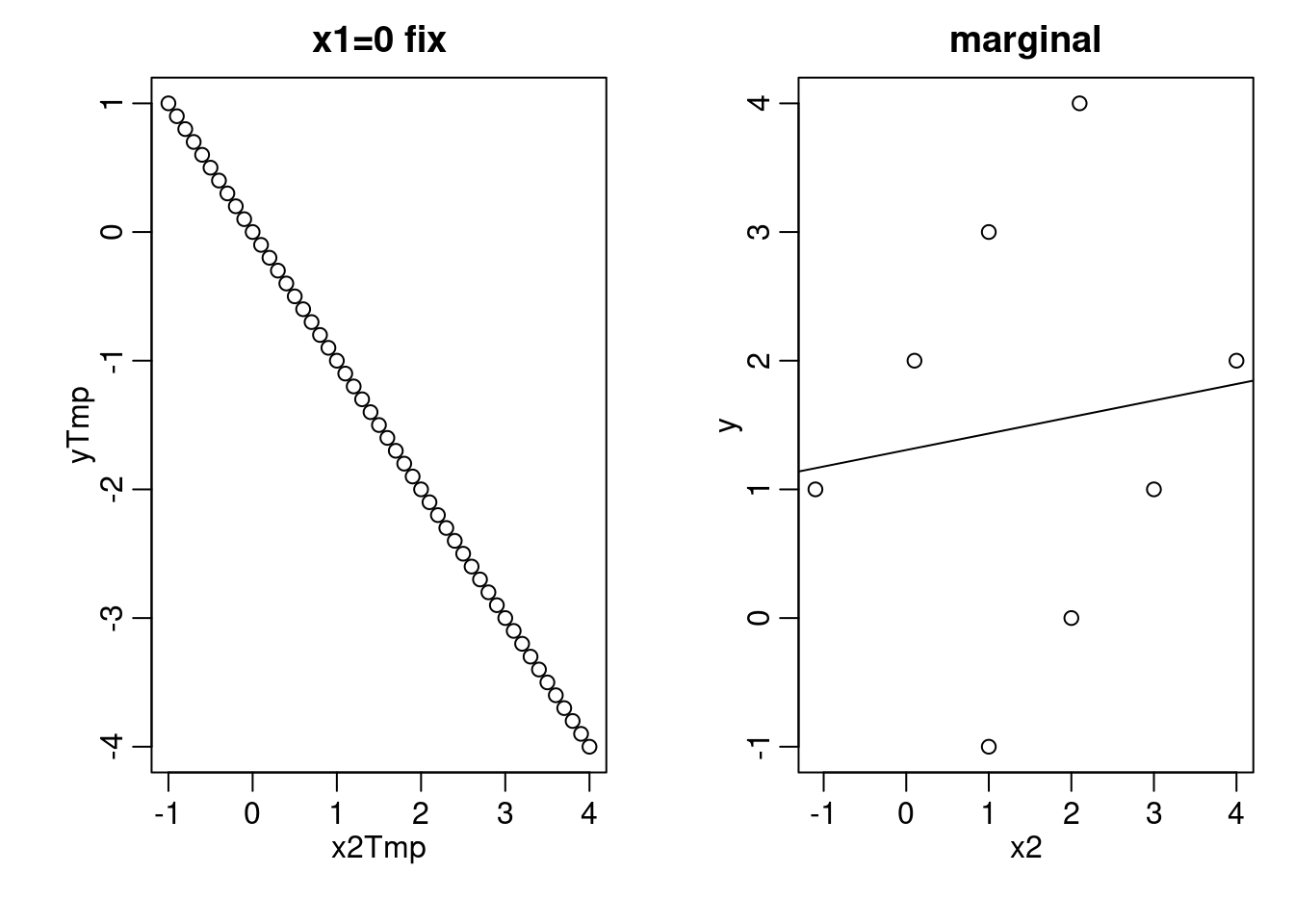

Realistische Beispiele, in denen einfache und multiple Regression wohl unterschiedliche Parameter schätzen würden (\(x1\) und \(x2\) sind vermutlich jeweils stark korreliert):

y: Lohn einer angestellten Person; x1: Alter der Person; x2: Dienstalter der Person; um z.B. zu untersuchen, ob junge Mitarbeiter bzgl. Lohn diskriminiert werden, wäre eine einfache Regression (Lohn vs. Alter) nicht angebracht. Wir müssten noch weitere erklärende Variablen in die Regression aufnehmen, die erklären können, warum jemand einen gewissen Lohn erhält (z.B. Ausbildung, Erfahrung, etc.). Von einer Dikriminierung könnten wir nur reden, wenn zwei Personen in unterschiedlichem Alter unterschiedlichen Lohn erhalten. Genau diese Aussage liefert die multiple Regression: Sie beschreibt den Zusammenhang zwischen Lohn und Alter . Welche Variablen genau in die Regression aufgenommen werden müssten, d.h., welche Variablen lohnrelevant sind, müssten Experten klären.
y: Preis von gebrauchtem Auto; x1: Alter in Jahren; x2: Gefahrene Kilometer.

2.5 Bsp 4: Transformationen

Sowohl die Zielvariable als auch die erklärenden Variablen können bei der linearen Regression transformiert werden. Auf diese Weise können die Modellvorraussetzungen häufig besser erfüllt werden. Allerdings muss die Interpretation der Parameter nach der Transformation sorgfältig erfolgen. Hier ein einfaches Beispiel. Wir versuchen einen Zusammenhang zwischen der Körpermasse (x) und der Gehirnmasse (y) von 35 Lebewesen zu finden.

dat <- read.csv(file = "animal.csv", header = TRUE)
plot(brain.g ~ body.kg, data = dat, xlab = "Koerpermasse [kg]",
     ylab = "Hirnmasse [g]")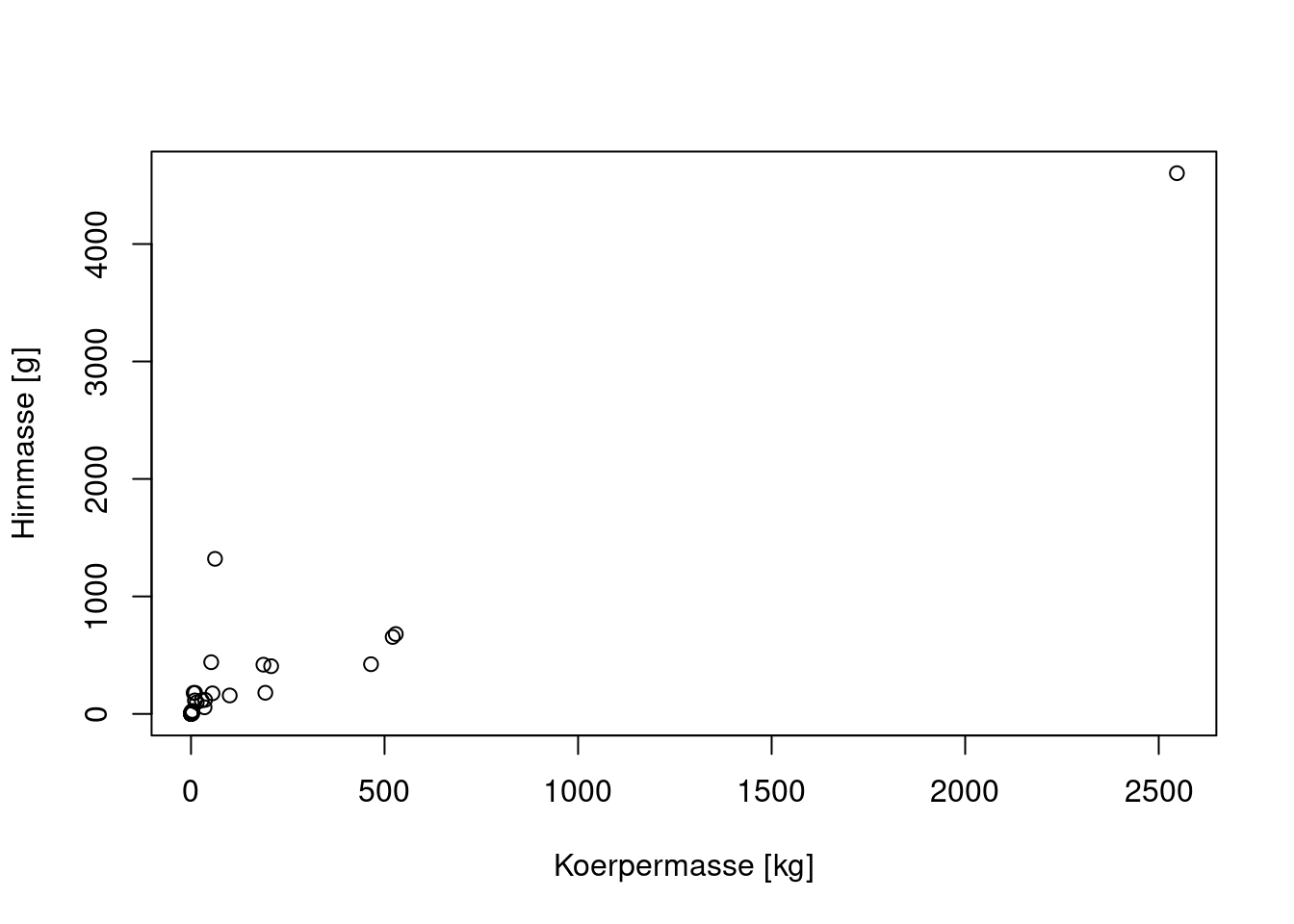

Die einfache lineare Regression passt sehr schlecht:

## x vs. y - Linearer Zusammenhang
fitAnimal <- lm(brain.g ~ body.kg, data = dat)
summary(fitAnimal)

## 
## Call:
## lm(formula = brain.g ~ body.kg, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -425.12  -47.78  -44.66   22.01 1165.29 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 48.03496   43.12841   1.114    0.273    
## body.kg      1.72062    0.09384  18.336   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 242.1 on 33 degrees of freedom
## Multiple R-squared:  0.9106, Adjusted R-squared:  0.9079 
## F-statistic: 336.2 on 1 and 33 DF,  p-value: < 2.2e-16

Die geschätzte Modellgleichung wäre in diesem Fall ungefähr: \(y = 48 + 1.7 \cdot x\). In den Residuenplots sehen wir allerdings, dass das Modell sehr schlecht passt:

par(mfrow = c(1, 2))
plot(fitAnimal, which = 1:2, ask = FALSE) ## Residuen

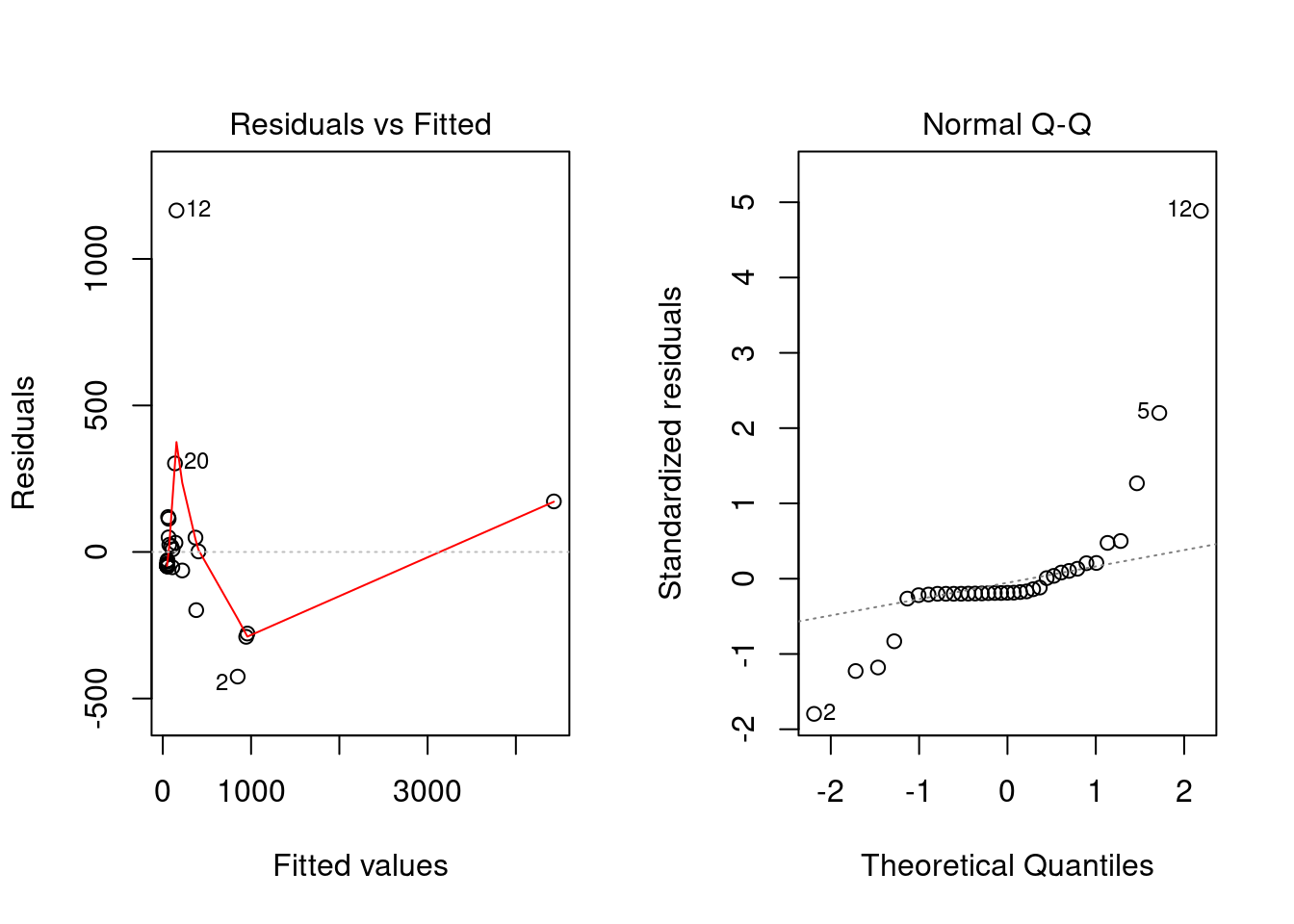
Nun versuchen wir es mit Transformationen. Zunächst transformieren wir die Zielgrösse. Das Streudiagramm sieht kaum besser aus:

plot(log(brain.g) ~ body.kg, data = dat)

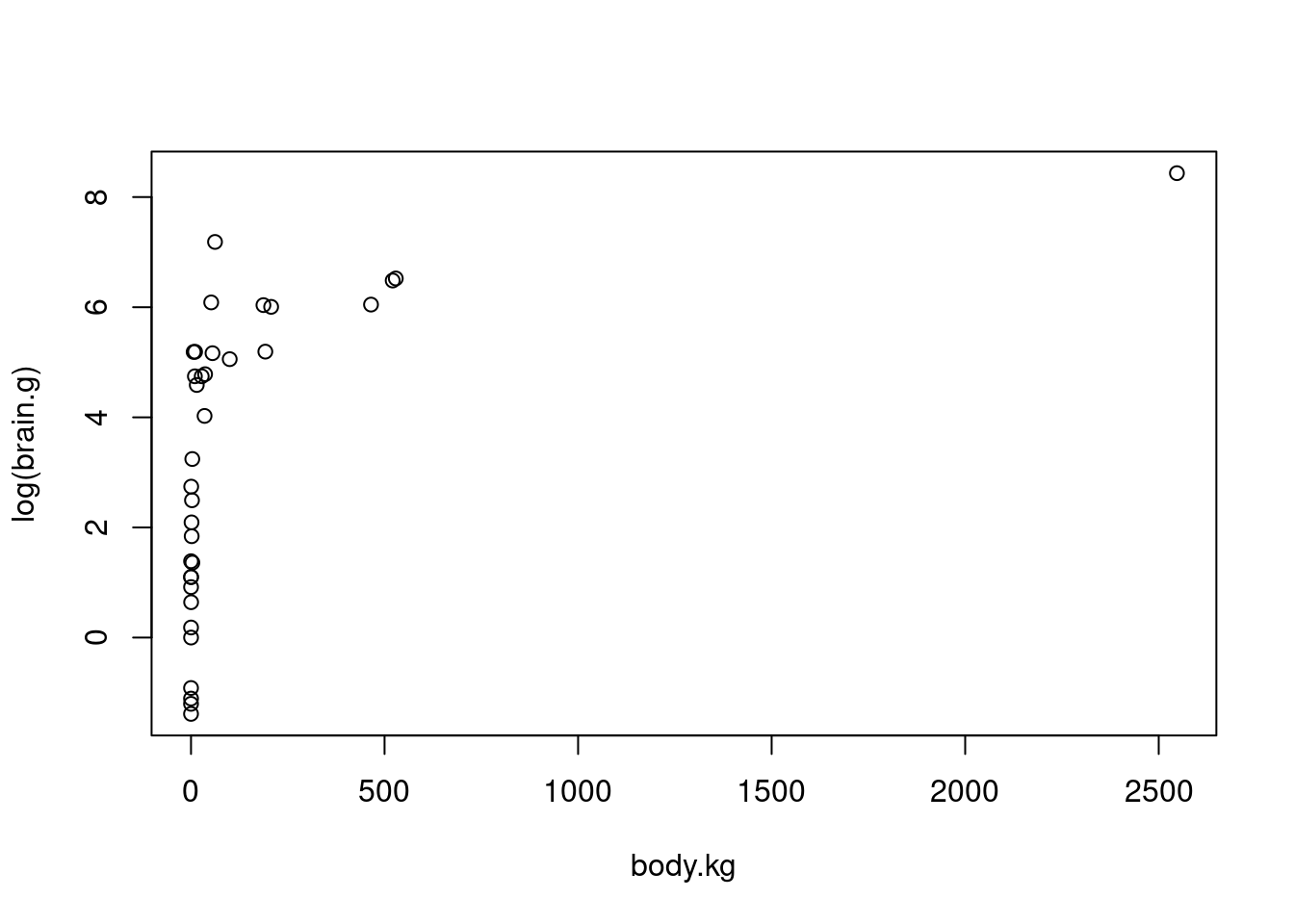
Nun berechnen wir die entsprechende Regression:

## x vs. log(y) - Exponentieller Zusammenhang
fitAnimalLog <- lm(log(brain.g) ~ body.kg, data = dat)
summary(fitAnimalLog)

## 
## Call:
## lm(formula = log(brain.g) ~ body.kg, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.2658 -1.8723  0.3533  1.9618  4.1204 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 2.8794544  0.4305599   6.688 1.29e-07 ***
## body.kg     0.0029924  0.0009368   3.194  0.00308 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.417 on 33 degrees of freedom
## Multiple R-squared:  0.2362, Adjusted R-squared:  0.213 
## F-statistic:  10.2 on 1 and 33 DF,  p-value: 0.00308

Die geschätzte Modellgleichung wäre in diesem Fall ungefähr: \(\log(y) = 2.88 + 0.003 \cdot x\) also umgeformt ein exponentieller Zusammenhang: \(y = \exp(2.88 + 0.003 \cdot x) \approx 17.8 \cdot \exp(0.003 \cdot x)\) (mit multiplikativem Fehlerterm). Die Residuenplots zeigen allerdings immer noch einen sehr schlechten Modellfit:

par(mfrow = c(1, 2))
plot(fitAnimalLog, which = 1:2, ask = FALSE) ## Residuen

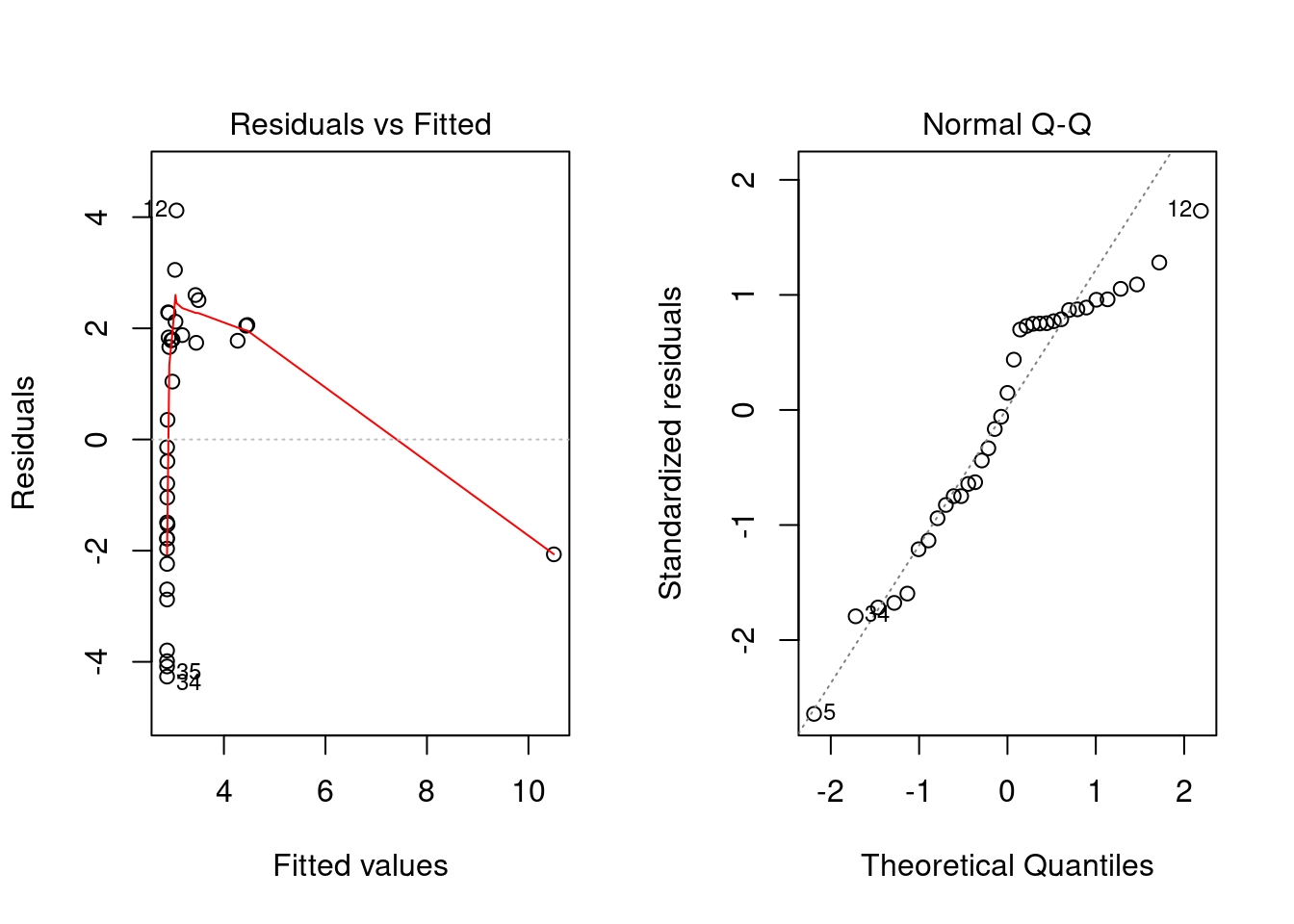
Schliesslich transformieren wir nun auch noch die erklärende Variable. Das Streudiagramm sieht wesentlich besser aus:

plot(log(brain.g) ~ log(body.kg), data = dat)

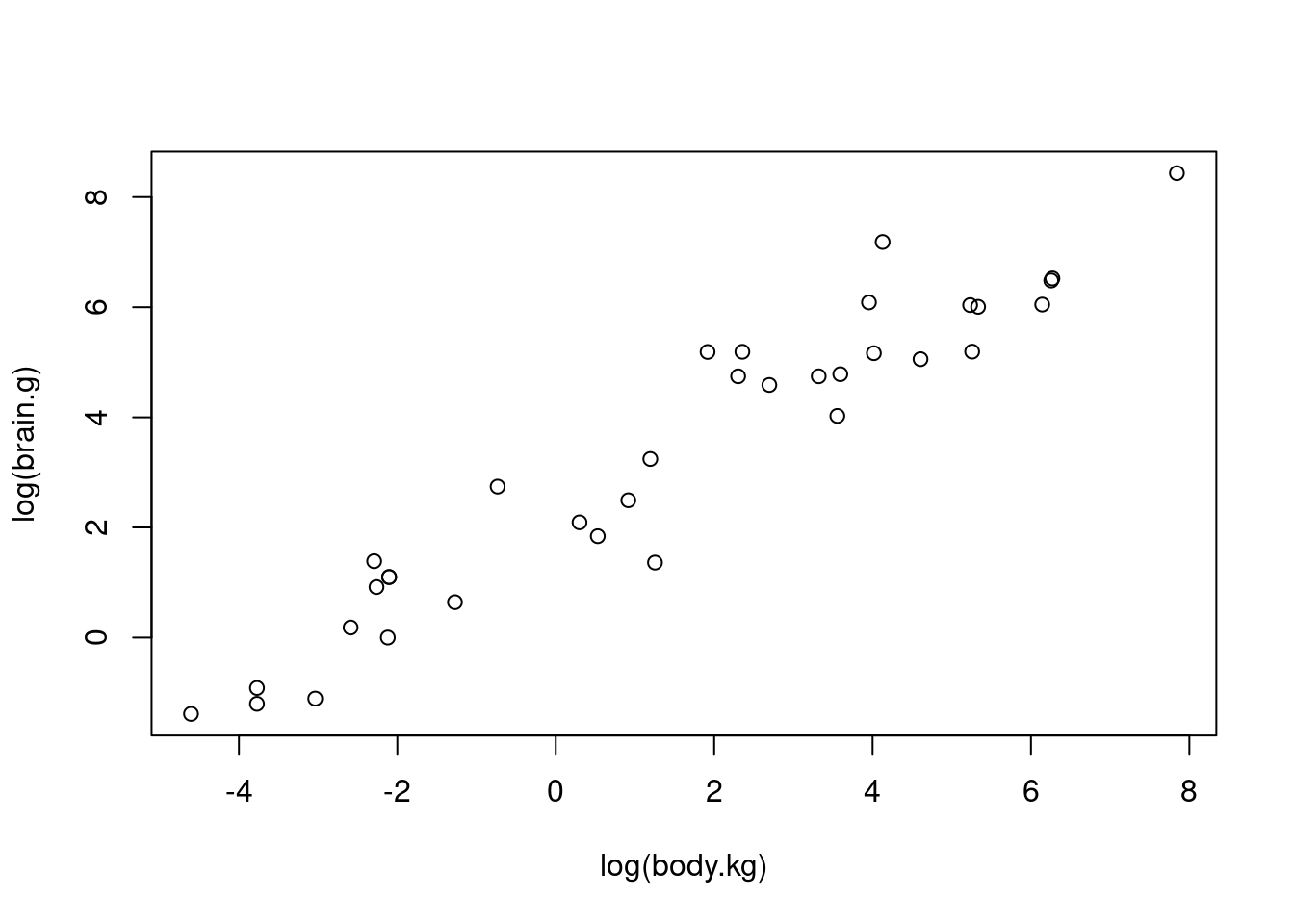
Nun berechnen wir die entsprechende Regresssion:

## log(x) vs. log(y) - Polynomieller Zusammenhang
fitAnimalLogLog <- lm(log(brain.g) ~ log(body.kg), data = dat)
summary(fitAnimalLogLog)

## 
## Call:
## lm(formula = log(brain.g) ~ log(body.kg), data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.7700 -0.5656 -0.1007  0.4673  1.8872 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.18647    0.14739   14.83 3.72e-16 ***
## log(body.kg)  0.75396    0.03959   19.05  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7987 on 33 degrees of freedom
## Multiple R-squared:  0.9166, Adjusted R-squared:  0.9141 
## F-statistic: 362.7 on 1 and 33 DF,  p-value: < 2.2e-16

Die geschätzte Modellgleichung wäre in diesem Fall ungefähr: \(\log(y) = 2.19 + 0.75 \cdot \log(x)\) also umgeformt ein polynomieller Zusammenhang: \(y = \exp(2.19 + 0.75 \cdot \log(x)) \approx 8.9 \cdot x^{0.75}\) (mit multiplikativem Fehlerterm). Die Residuenplots zeigen nun einen sehr guten Modellfit:

par(mfrow = c(1, 2))
plot(fitAnimalLogLog, which = 1:2, ask = FALSE)

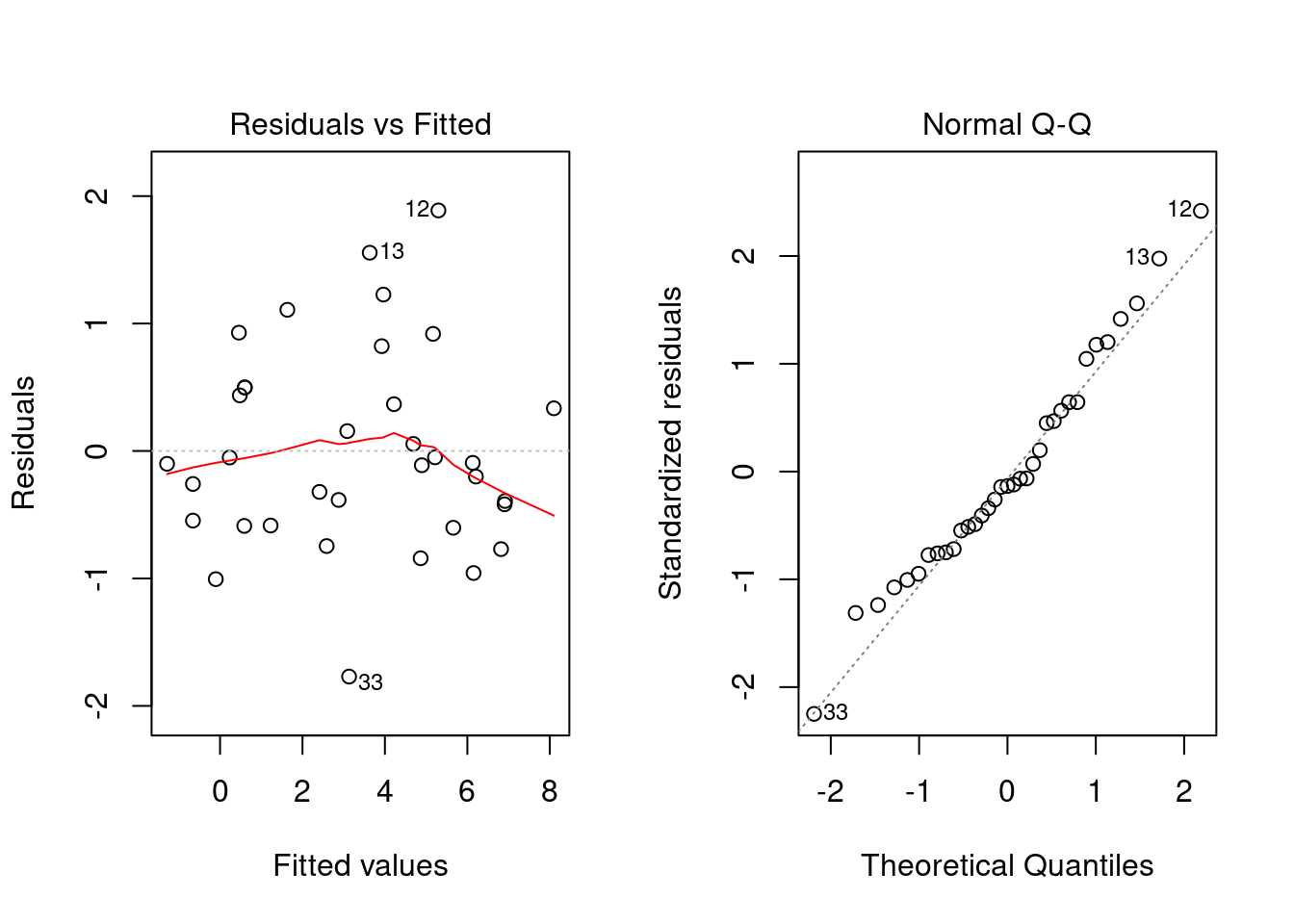
Wir sehen also, dass mit Transformationen manchmal ein sehr gut passendes Modell gefunden werden kann. Allerdings muss man beim Interpretieren der Parameter sehr vorsichtig sein.

Vertrauensintervalle können leicht berechnet werden, indem einfach die Grenzen der Vertrauensintervalle entsprechend mittransformiert werden (das gilt für alle monotonen Transformationen). Im letzten Beispiel haben wir z.B. das Modell \(\log(y) = \beta_0 + \beta_1 \cdot \log(x)\) gefittet. Vertrauensintervalle für \(\beta_0\) und \(\beta_1\) sind einfach verfügbar:

confint(fitAnimalLogLog, level = 0.95)

##                  2.5 %    97.5 %
## (Intercept)  1.8865949 2.4863417
## log(body.kg) 0.6734206 0.8344992

Anschliessend haben wir das Modell umgeformt zu: \(y = a \cdot b^y\). Wie können wir Vertrauensintervalle für \(a\) und \(b\) bestimmen? Dazu müssen wir zunächst herausfinden, wie sich \(a\) und \(b\) aus \(\beta_0\) und \(\beta_1\) berechnen lassen. In unserem Fall: \(a = \exp(\beta_0)\) und \(b = \beta_1\) (beides monotone Transformationen). Genau die gleiche Transformation wenden wir nun auf die Endpunkte der Vertrauensintervalle von \(\beta_0\) bzw. \(\beta_1\) an:

ci <- confint(fitAnimalLogLog, level = 0.95)
exp(ci[1,]) ## 95%-VI für a

##     2.5 %    97.5 % 
##  6.596867 12.017233

ci[2,] ## 95%-VI für b

##     2.5 %    97.5 % 
## 0.6734206 0.8344992

Entsprechend ist ein 95%-Vertrauensintevall für \(a\) ungefähr \([6.6, 12.0]\) und für \(b\) ungefähr \([0.67, 0.83]\).

2.6 Bsp 5: Kollinearität

Wenn zwei erklärende Variablen sehr stark korreliert sind (oder auch mehr als zwei Variablen linear abhängig sind), kann es vorkommen, dass kein einziger \(t\)-Test (testet \(H_{0,j}: \beta_j = 0\) für einen bestimmten Parameter \(\beta_j\)) im summary-output signifikant ist, der \(F\)-Test aber schon (dieser testet \(H_0: \beta_1 = \beta_2 = ... = \beta_{p-1} = 0\)). Denn gegeben die eine Variable kann die andere Variable kaum mehr etwas zum Modell beitragen (siehe dazu auch das Konzept des “Variance Inflation Factor”). Die einfachste Lösung bei zwei stark korrelierten Variablen besteht darin, eine von beiden wegzulassen. Im Folgenden geben wir ein kleines simuliertes Beispiel:

## Simuliere Daten
set.seed(123)
n <- 100
x1 <- rnorm(n)
x2 <- x1 + rnorm(n, sd = 0.1)
cor(x1, x2) ## sehr stark korreliert

## [1] 0.9943911

y <- x1 + x2 + rnorm(n)
## Werte Daten aus
## einzelne Parameter nicht signifikant, F-Test aber schon
summary(lm(y ~ x1 + x2))

## 
## Call:
## lm(formula = y ~ x1 + x2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.8730 -0.6607 -0.1245  0.6214  2.0798 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  0.13507    0.09614   1.405    0.163
## x1           0.62872    0.99031   0.635    0.527
## x2           1.23811    0.98995   1.251    0.214
## 
## Residual standard error: 0.9513 on 97 degrees of freedom
## Multiple R-squared:  0.7657, Adjusted R-squared:  0.7609 
## F-statistic: 158.5 on 2 and 97 DF,  p-value: < 2.2e-16

summary(lm(y ~ x1)) ## einzelner Parameter ist signifikant

## 
## Call:
## lm(formula = y ~ x1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.9198 -0.6413 -0.1380  0.5539  2.1101 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.12234    0.09587   1.276    0.205    
## x1           1.86033    0.10504  17.710   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.954 on 98 degrees of freedom
## Multiple R-squared:  0.7619, Adjusted R-squared:  0.7595 
## F-statistic: 313.7 on 1 and 98 DF,  p-value: < 2.2e-16

summary(lm(y ~ x2)) ## einzelner Parameter ist signifikant

## 
## Call:
## lm(formula = y ~ x2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.84964 -0.70758 -0.09879  0.61418  2.15980 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.1421     0.0952   1.493    0.139    
## x2            1.8631     0.1044  17.848   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9484 on 98 degrees of freedom
## Multiple R-squared:  0.7647, Adjusted R-squared:  0.7623 
## F-statistic: 318.6 on 1 and 98 DF,  p-value: < 2.2e-16

2.7 Bsp 6: Training- und Test-Error

Wir erklären den Unterschied zwischen Training- und Test-Error mit einem Beispiel aus der Regression. Das zu Grunde liegende Prinzip ist aber weit über die Regression hinaus gültig.

Wir starten mit einem wahren Modell: \(y = 1 + 2 \cdot x + \varepsilon\) mit \(\varepsilon \sim N(0,1)\). Wir simulieren \(10\) Punkte von diesem Modell und zeigen in rot das wahre Modell. In schwarz sehen wir die mit den Daten geschätzte Regressionsgerade. In blau ist ein mit den Daten geschätztes Polynom 7. Grades gezeigt.

## Simuliere Daten
set.seed(123)
n <- 10
x <- seq(0, 1, length.out = n)
y <- 1 + 2 * x + rnorm(n)

## Plotte Daten
plot(x, y)
abline(a = 1, b = 2, col = "red")

## Fit einer einfachen linearen Regression
fmLin <- lm(y ~ x)
abline(fmLin)

## Fit einer komplizierten multiplen Regression (Polynom 7. Grades)
## poly(x,k) erzeugt ein Polynom k-ten Grades in x

fmPoly <- lm(y ~ poly(x, 7)) 
xTmp <- seq(0, 1, by = 0.01)
yTmp <- predict(fmPoly, newdata = data.frame(x = xTmp))
points(xTmp, yTmp, col = "blue", type = "l")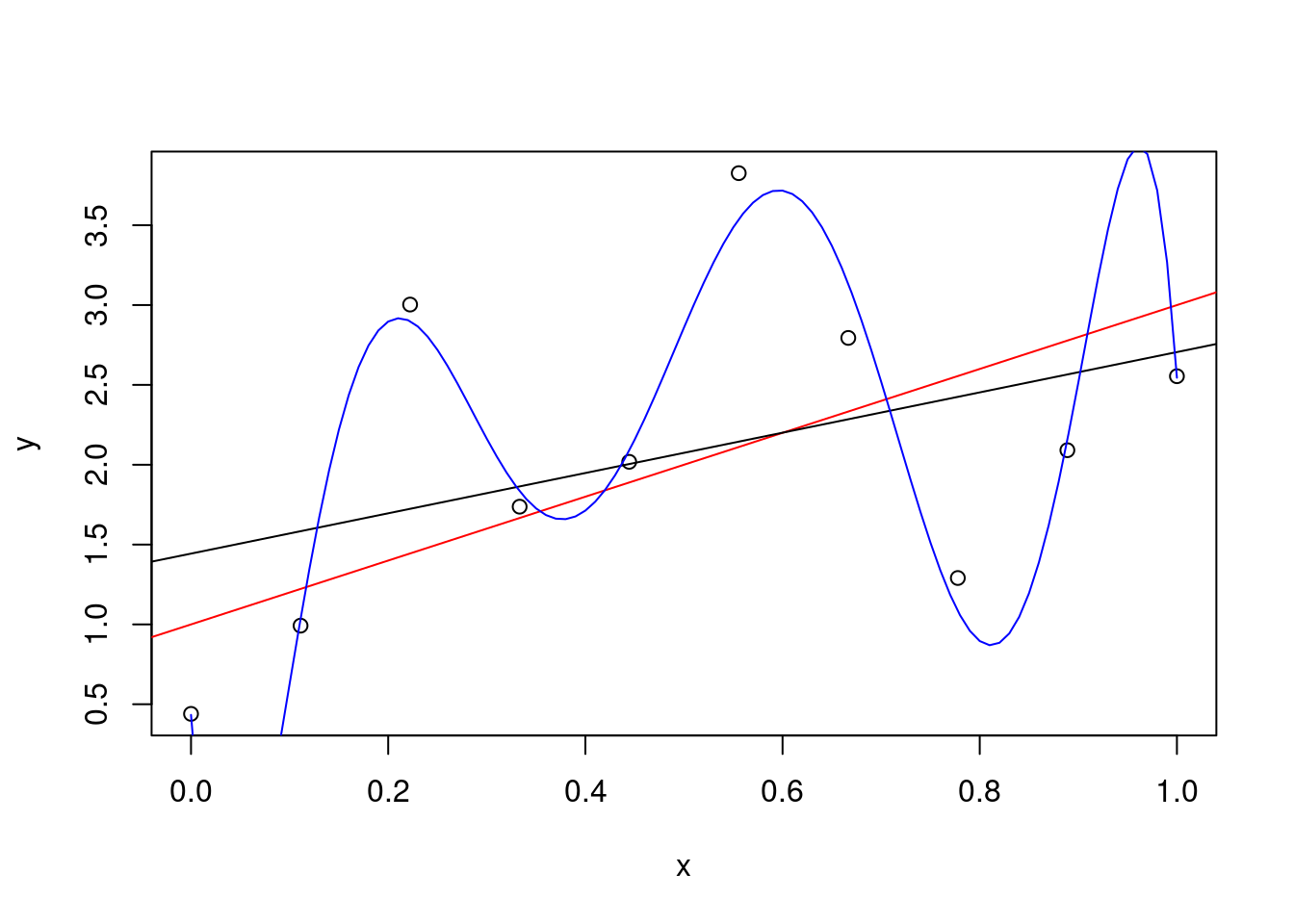

Wir sehen, dass die blaue Kurve den Punkten sehr viel näher kommt als die schwarze Kurve (geschätzte Regression) und sogar die rote Kurve (wahres Modell). Der Trainingserror für die blaue Kurve is entsprechend viel kleiner als der Trainingserror für die schwarze Kurve:

## Trainings MSE: einfaches Modell
mean((predict(fmLin) - y)^2)

## [1] 0.7632995

## Trainings MSE: kompliziertes Modell
mean((predict(fmPoly) - y)^2)

## [1] 0.02723261

Obwohl das blaue Modell bzgl. Trainings-MSE viel besser wirkt, sehen wir, dass es den Fehlern “hinterher rennt” und mit dem wahren Modell (rote Kurve) nicht mehr viel zu tun hat. Dieses Verhalten nennt man “Overfitting”. Entsprechend schlecht wird das komplizierte Modell auf neuen Daten vom gleichen Modell (Testdaten) funktionieren. Wir berechnen nun den Test-Error:

set.seed(123)

## Viele neue Daten vom gleichen Modell
n <- 1000
xNew <- runif(n, min = 0, max = 1)
yNew <- 1 + 2 * xNew + rnorm(n) 

## Test MSE: einfaches Modell
mean((predict(fmLin) - yNew)^2)

## [1] 1.522989

## Test MSE: kompliziertes Modell
mean((predict(fmPoly) - yNew)^2)

## [1] 2.169131

Wie erwartet, schneidet das komplizierte Modell auf den (neuen) Testdaten bei weitem nicht mehr so gut ab wie auf den Trainingsdaten - die Enttäuschung ist gross! Wenn wir die Vorhersagequalität eines Modells abschätzen wollen, ist es also wichtig den Testerror und nicht nur den Trainingserror zu untersuchen. Dazu kann z.B. Kreuzvaliedierung verwendet werden.

2.8 Bsp 7: LOOCV

Wir zeigen nun, wie man die Leave-One-Out Cross-Validation (LOOCV) manuell bzw. mit der Funktion cv.glm ausführen kann (mit dieser Funktion kann auch k-fold CV durchgeführt werden). Dazu simulieren wir zunächst Daten von einem einfachen Modell. Dann schätzen wir den Test-Error mit einem Testdatensatz (das könnten wir in der Praxis natürlich nicht machen, weil wir üblicherweise keine Testdaten haben und deshalb CV machen). Anschliessend schätzen wir den Test-Error an Hand der Trainingsdaten indem wir LOOCV verwenden (nur diesen Schritt würden wir in der Praxis machen). Dazu kommt einmal die Fuktion zum Einsatz; dann zeigen wir, wie man die LOOCV manuell programmieren könnte. Das Ergebnis ist identisch. Da wir in diesem Beispiel ein sehr einfaches Modell verwenden, kommt es zu keinem spürbaren Overfitting, d.h., der Trainingserror ist selber schon vergleichbar mit dem Testerror. In der Praxis kann man sich bei komplexeren Modellen nicht sicher sein, ob es zu Overfitting kommen wird oder nicht. Daher ist es immer eine gute Idee den Testerror mit einer Art von Kreuzvalidierung (und nicht mit dem Trainingserror) zu bestimmen.

## Erzeuge einen Trainings Datensatz
set.seed(123)
n <- 1000
x <- runif(n, min = 0, max = 1)
y <- 1 + x + rnorm(n)
dat <- data.frame(x = x, y = y)

## Fitte Modell auf Trainingsdaten
fm <- lm(y ~ x, data = dat)

## Erzeuge einen Test Datensatz
xTest <- runif(n, min = 0, max = 1)
yTest <- 1 + xTest + rnorm(n)
datTest <- data.frame(x = xTest, y = yTest)

## Test Error (MSE) mit Test set:
mean((predict(fm) - yTest)^2) ## Test error

## [1] 1.099524

## Training error: Weil das Modell so einfach ist, 
## erwarten wir KEIN Overfitting
mean((predict(fm) - y)^2)

## [1] 1.00175

library(boot)
## re-fitte mit glm(), sodass wir cv.glm() verwenden können
fmGLM <- glm(y ~ x, data = dat) 
cvErr <- cv.glm(fmGLM, data = dat)
cvErr$delta[1] ## Geschätzter Test Error mit LOOCV

## [1] 1.0058

## das gleiche manuell
pred <- rep(NA, nrow(dat))
for (i in 1:nrow(dat)) {
  fmTmp <- lm(y ~ x, data = dat[-i,])
  pred[i] <- predict(fmTmp, newdata = data.frame(x = x[i]))
}
mean( (pred - dat$y)^2 ) ## Gleicher Wert wie mit cv.glm()

## [1] 1.0058

2.9 Bsp 8: Model Selection

Es gibt verschiedene Kriterien um zu entscheiden, welches von mehreren geschätzten Modellen dem wahren Modell am nächsten kommt bzw. auf zukünftigen Daten die besten Vorhersagen machen wird. Einige Beispiele sind \(AIC\), \(BIC\), Mallow’s \(C_p\). All diese Kriterien wägen zwei Faktoren ab: Wie gut passt das Modell und wie viele Parameter verwendet das Modell. Intuitiv merkt man sich diese Kriterien am einfachsten als geschätzten “Abstand vom wahren Modell” (der Vergleich mit dem Abstand hinkt etwas: Die Kriterien können auch negativ werden; dennoch gilt: je kleiner, desto besser). Wir werden im Folgenden zeigen, wie Modellwahl mit \(BIC\) durchgeführt werden kann. Wenn ein geschätztes Modell ein kleines \(BIC\) hat, ist der “Abstand” zum wahren Modell also klein und es handelt sich um ein “gutes” Modell. Üblicherweise wählt man aus allen Kandidaten-Modellen das Modell mit dem kleinsten \(BIC\) aus. Wenn man sehr viele Daten zur Verfügung hat, kann dieser Abstand zuverlässig geschätzt werden. Gibt es allerdings nicht viele Daten, muss man leider davon ausgehen, dass der Abstand nicht sehr zuverlässig geschätzt wird. Hier ein Beispiel:

Zuerst simulieren wir Daten vom wahren Modell \(y = x_1 + x_3 + \varepsilon\), wobei \(\varepsilon \sim N(0,1)\). Zudem erzeugen wir Variablen, die mit der Zielgrösse \(y\) gar nichts zu tun haben: \(x_2, x_4, x_5\).

set.seed(123)
n <- 1e5 ## 100'000 Daten
x1 <- runif(n)
x2 <- runif(n)
x3 <- runif(n)
x4 <- runif(n)
x5 <- runif(n)
y <- x1 + x3 + rnorm(n)
d <- data.frame(x1 = x1, x2 = x2, x3 = x3, x4 = x4, x5 = x5, y = y)

Da wir die Daten simulieren, wissen wir also, dass das wahre Modell \(y = 1 \cdot x_1 + 1 \cdot x_3\) ist. Im Datensatz gibt es allerdings noch die erklärenden Variablen \(x_2\), \(x_4\) und \(x_5\). Sie haben nichts mit der Zielgrösse \(y\) zu tun. In der Praxis wüssten wir das natürlich nicht und müssten jetzt aus den Variablen \(x_1, \ldots, x_5\) die wichtigsten (“wahren”) Einflussgrössen finden. Dazu berechnen wir alle Modelle, die mit den 5 erklärenden Variablen denkbar wären (also z.B. nur \(x_1\) oder \(x_1 + x_2\) etc.; insgesamt sind das \(2^p\) Modelle, wenn wir \(p\) Variablen haben; wenn \(p\) gross wird, gibt es also schnell sehr viele mögliche Modelle). Für jedes Modell berechnen wir \(BIC\) und wählen am Schluss das Modell mit dem kleinsten \(BIC\). Leider können wir in der Praxis nicht prüfen, ob \(BIC\) ein gutes Modell gefunden hat. In der Simulation aber können wir das gefundene Modell mit dem wahren Modell vergleichen.

library(leaps)
## es werden ALLE möglichen Modelle inkl BIC berechnet
m1 <- regsubsets(y ~ ., data = d, method = "exhaustive") 
summary(m1)

## Subset selection object
## Call: regsubsets.formula(y ~ ., data = d, method = "exhaustive")
## 5 Variables  (and intercept)
##    Forced in Forced out
## x1     FALSE      FALSE
## x2     FALSE      FALSE
## x3     FALSE      FALSE
## x4     FALSE      FALSE
## x5     FALSE      FALSE
## 1 subsets of each size up to 5
## Selection Algorithm: exhaustive
##          x1  x2  x3  x4  x5 
## 1  ( 1 ) "*" " " " " " " " "
## 2  ( 1 ) "*" " " "*" " " " "
## 3  ( 1 ) "*" " " "*" "*" " "
## 4  ( 1 ) "*" " " "*" "*" "*"
## 5  ( 1 ) "*" "*" "*" "*" "*"

Für jede Anzahl Variablen wird uns nun das beste Modell (d.h. kleinstes BIC) angezeigt. Wenn wir z.B. ein Modell mit nur einer einzigen Variablen wollen, müssten wir das Modell \(y = x_1\) wählen. Wenn wir ein Modell mit genau drei Variablen wollen, müssten wir das Modell \(y = x_1 + x_3 + x_4\) wählen. Welches von diesen fünf vorgeschlagenen Modellen kommt dem wahren Modell wohl am nächsten? Schauen wir uns für jedes dieser 5 Modelle die \(BIC\)-Werte an:

m1s <- summary(m1)
m1s$bic

## [1]  -7373.192 -15223.163 -15213.274 -15202.568 -15191.438

Wir erinnern uns: Kleine Werte bzgl. \(BIC\) stehen für ein gutes Modell. Das Modell mit dem kleinsten \(BIC\) ist das Modell, das als zweites aufgelistet wird, also zwei Variablen hat. Im summary output von oben sehen wir, dass es sich um das Modell \(y = x_1 + x_3\) handelt. Wir haben tatsächlich das wahre Modell gefunden !

Für die Praxis muss man die Euphorie leider etwas dämpfen: In der Praxis gelingt es selten, das “wahre” Modell zu finden. Entweder ist das wahre Modell z.B. nicht in unserem Suchraum (z.B. könnte das wahre Modell \(y = \sin(x_1)\) sein; dieses Modell haben wir oben nicht ausprobiert) oder wir haben zu wenige Daten, um den Abstand zum wahren Modell zuverlässig abschätzen zu können. In diesem Beispiel hatten wir immerhin 100’000 Datenpunkte und aus nur 5 Variablen auszuwählen - ein denkbar günstiges Setting. Mit weniger Datenpunkten wären wir nicht so erfolgreich gewesen. Angenommen, wir hätten nur die ersten 20 Datenpunkte gemessen:

d2  <- d[1:20,]
m2  <- regsubsets(y ~ ., data = d2, method = "exhaustive")
m2s <- summary(m2)
m2s

## Subset selection object
## Call: regsubsets.formula(y ~ ., data = d2, method = "exhaustive")
## 5 Variables  (and intercept)
##    Forced in Forced out
## x1     FALSE      FALSE
## x2     FALSE      FALSE
## x3     FALSE      FALSE
## x4     FALSE      FALSE
## x5     FALSE      FALSE
## 1 subsets of each size up to 5
## Selection Algorithm: exhaustive
##          x1  x2  x3  x4  x5 
## 1  ( 1 ) "*" " " " " " " " "
## 2  ( 1 ) "*" " " "*" " " " "
## 3  ( 1 ) "*" " " "*" "*" " "
## 4  ( 1 ) "*" " " "*" "*" "*"
## 5  ( 1 ) "*" "*" "*" "*" "*"

m2s$bic

## [1] -1.8840253 -1.4543132  0.4956058  1.9526454  4.9459919

Nun wird das erste Modell (\(y = x_1\)) als das beste Modell bestimmt. Wir haben das wahre Modell also verfehlt. Dennoch wird \(BIC\) und \(AIC\) sehr häufig verwendet um vielleicht nicht gerade das wahre, aber doch ein möglichst gut passendes Modell zu finden.

Mit obiger Option “exhausitve” werden alle möglichen Submodelle berechnet. Wenn man viele Variablen hat, ist das rein rechentechnisch nicht mehr machbar (z.B. gibt es bei 20 Variablen schon \(2^{20} \approx 10^6\) Modelle zu berechnen). In diesen Fällen kann man mit der Option “backward” oder “forward” nur einen kleinen Teil des Suchraums durchsuchen (“forward” startet bei dem leeren Modell, also y ~ 1 und “backward” startet bei dem vollen Modell, also y ~ .). Diese Methoden lassen sich auch mit hunderten von Variablen problemlos berechnen. Allerdings bezahlt man den Preis, dass man eben nicht mehr alle möglichen Modelle durchsucht. Selbst wenn das wahre Modell im Suchraum wäre, würde man es evtl. verpassen. Auch hier gilt wieder: Pragmatischerweise wird diese Methode dennoch sehr häufig verwendet um einfach ein möglichst brauchbares Modell unter vielen Möglichen zu finden.