8 Principal Component Analysis (PCA)

8.1 Theorie in Kürze

  • Explorativ; finde “günstigere” Basis um Daten darzustellen
  • Wichtigste Richtung: Richtung, entlang der die Daten am meisten streuen => PC 1
  • Jeder nächste PC ist senkrecht zu allen vorhergehenden und zeigt wieder in die Richtung mit der grössten Streuung
  • Maximale Anzahl PCs: min( Anzahl Variablen, Anzahl Samples-1 )
  • Daten vor PCA immer zentrieren; wenn Variablen unterschiedliche Einheiten haben => Daten vor PCA skalieren
  • Häufig behält man nur so viele PCs, sodass die Varianz der Originaldaten noch hinreichend gut (z.B. 80% der Originalvarianz) erklärt werden kann

  • Wichtige Begriffe: loadings - Richtungen der PCs; rotation - Matrix des Basiswechsels zw Standardbasis und PC-Basis; score/x: Koordinaten der Datenpunkte bzgl. der PC Basis

  • Wichtige R Funktionen: , auf das Ergebnis von ;

8.2 PCA

In diesem Beispiel illustrieren wir die PCA an einem simulierten Datensatz. Wir haben 20 Datenpunkte mit je 4 gemessenen Variablen (alle in den gleichen Einheiten):

##             [,1]       [,2]       [,3]       [,4]
## [1,] -2.08854125  0.9945028  3.1685464  1.9460013
## [2,]  0.06302571 -0.2492105  1.4722295  0.1608045
## [3,] -6.22532542 -2.6973743 -1.3436473 -3.3158995
## [4,]  0.45314749 -4.1810887 -0.5526860  3.2633864
## [5,] -0.15234883 -3.3016491  0.1266672  1.6598566
## [6,] -8.27469714 -2.9651164 -1.5712595 -2.0273594

Nun führen wir die PCA durch (per Konvention werden die Daten vor der PCA immer zentriert; mit skaliert werden sie nur, wenn die Einheiten unterschiedlich sind, was hier nicht der Fall ist):

## List of 5
##  $ sdev    : num [1:4] 4.03 2.66 2 1.48
##  $ rotation: num [1:4, 1:4] 0.596 0.341 0.578 0.44 -0.618 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
##  $ center  : num [1:4] -0.247 -0.529 -0.316 -0.12
##  $ scale   : logi FALSE
##  $ x       : num [1:20, 1:4] 2.344 1.437 -6.307 0.526 0.151 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4"
##  - attr(*, "class")= chr "prcomp"

In dem resultierenden Objekt sind die wesentlichen Informationen der PCA gespeichert:

  • : Standardabweichungen in den Richtungen der PCs; wenn man die Daten auf PC1 projiziert, haben die projizierten Datenpunkte eine Standardabweichung entlang PC1 von 4.03; die Standardabweichung entlang PC2 ist nur 2.66, entlang PC3 nur 2 und entlang PC4 nur 1.48; per Konstruktion der PCs ist also in der Tat die Streuung entlang PC1 am grössten und nimmt mit jedem weiteren PC ab. Insbesondere gibt es keine Richtung im 4-dim Raum, entlang der die Standardabweichung grösser als 4.03 wäre, denn PC1 ist gerade als die Richtung mit der grössten Streuung konstruiert worden.
  • : Matrix des Basiswechsels von der PC Basis zur Standardbasis. Die Spalten sind die Loadings, also die Richtungen der PCs bzgl. der Standardbasis
  • : Die Koordinaten der Datenpunkte bzgl. der PC Basis

Ein Ziel der PCA ist es häufig, die “wichtigsten” Richtungen zu behalten und die unwichtigen einfach wegzulassen. In diesem Sinne würden wir die ersten paar PCs behalten und die übrigen einfach weglassen.

Ein extremes Beispiel dafür ist der Biplot: Er behält nur die ersten beiden PCs und plottet die Datenpunkte dann in dieser Ebene. Obwohl das die Ebene mit der grössten Streuung ist, sollte klar sein, dass dabei sehr viel Information verloren gehen kann. Es gibt viele Varianten des Biplots und wir gehen hier nicht auf die Details ein.

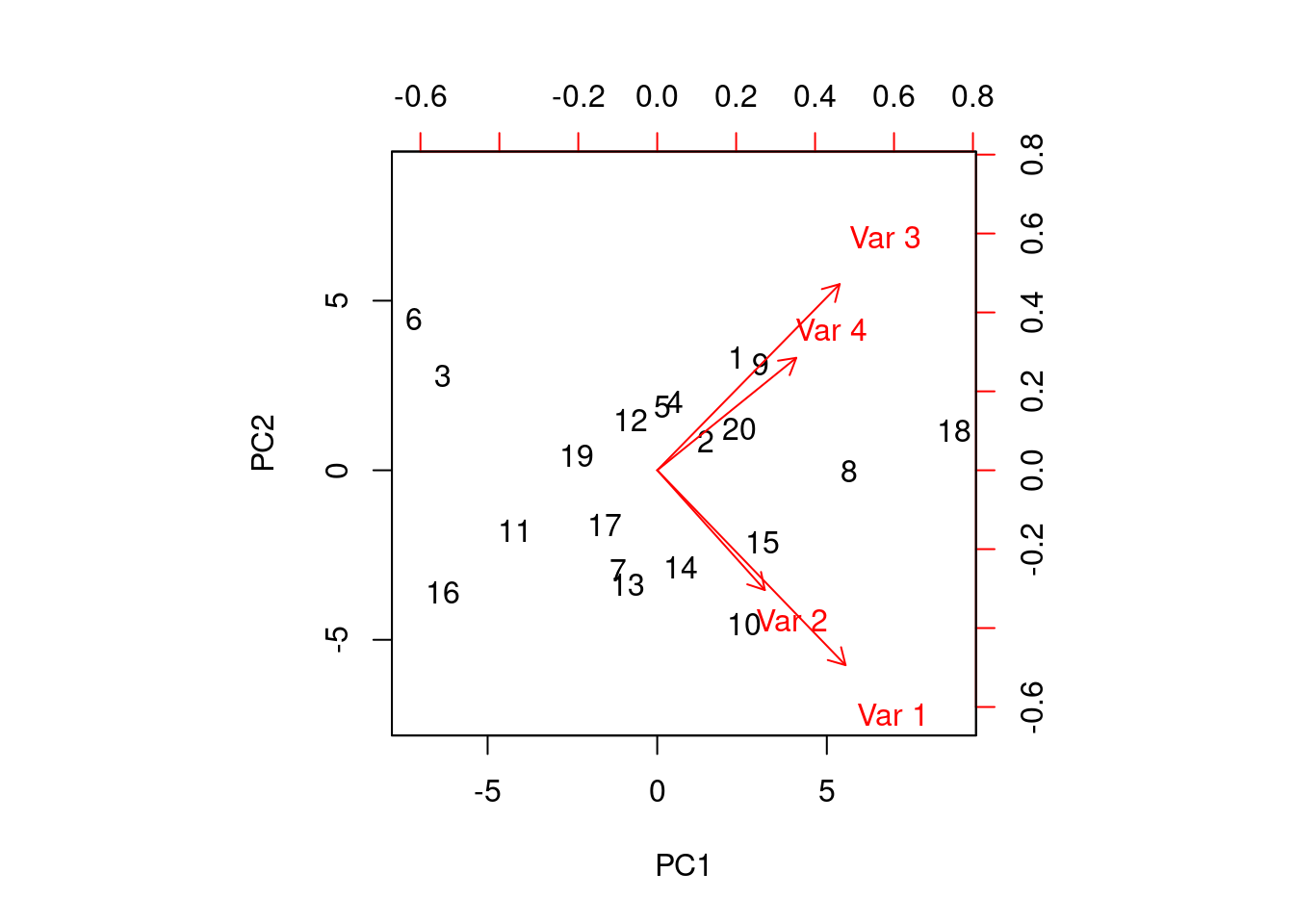
Um zu entscheiden, wie viele PCs man behalten will, schaut man sich die Streuung entlang der einzelnen PCs an.

## Importance of components:
##                           PC1    PC2    PC3     PC4
## Standard deviation     4.0283 2.6553 2.0005 1.48122
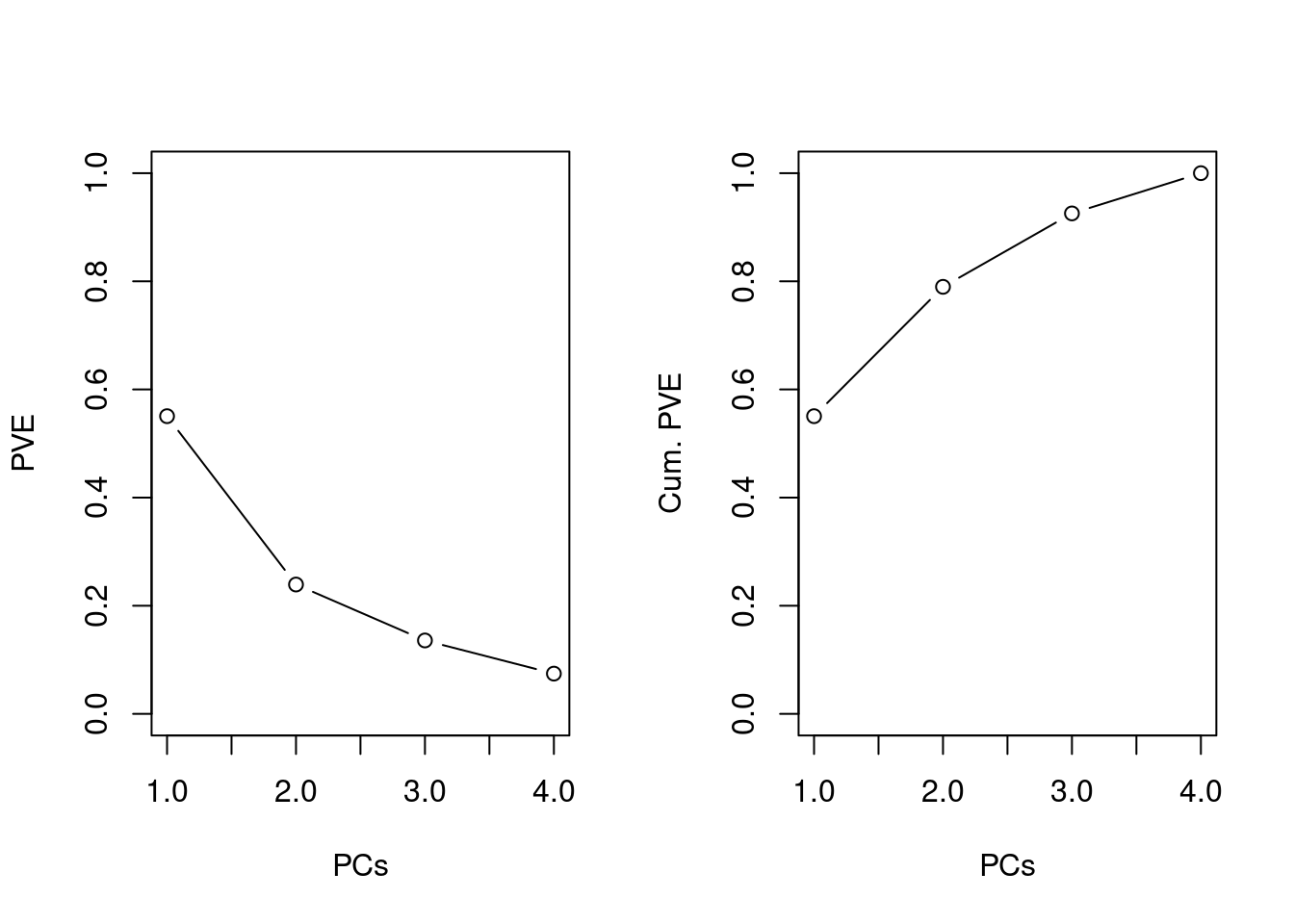
## Proportion of Variance 0.5506 0.2392 0.1358 0.07444
## Cumulative Proportion  0.5506 0.7898 0.9256 1.00000

Wir sehen: Die Standardabweichungen entlang PC1 bis PC4 sind \(4.0283\), \(2.6553\), \(2.0005\) und \(1.48122\). Die Varianzen entlang der PCs sind entsprechend die quadrierten Werte: \(16.2275\), \(7.0508\), \(4.0022\) und \(2.1940\). Wenn man all diese Varianzen zusammenzählt, erhält man eine “totale” Varianz von \(29.4745\). Je wichtiger ein PC, desto grösser ist der Anteil der Varianz entlang der PC verglichen mit der totalen Varianz (denken Sie an die Extreme: Wenn alle Punkte entlang einer Geraden aufgereiht sind, entspricht diese Gerade der PC 1 und die Varianz entlang PC 1 entspricht der totalen Varianz; d.h., PC 1 erklärt schon alles und wir brauchen keine weiteren PCs mehr).

Der Anteil jeder PC an der totalen Varianz wird in der zweiten Zeile “Proportion of Variance” angezeigt: \(16.2275 / 29.4745 \approx 0.5506\) etc. Wenn man die Daten statt in 4 Dimensionen nur mit den ersten beiden PCs erklären würde, könnten wir \(0.5506 + 0.2392 = 0.7898\) der totalen Varianz erklären. Diese “zusammengezählten” Anteile der erklärten Varianz werden in der dritten Zeile (“Cumulative Proportion”) aufgelistet.

Wenn wir z.B. mindestens 80% der totalen Varianz erklären wollen, müssen wir also die ersten 3 PCs verwenden: Mit nur einer PC erklären wir nur 55%, mit den ersten beiden PCs schon 78% und mit den ersten 3 PCs 93% der totalen Varianz (mit allen 4 PCs würden wir die Datenpunkte perfekt beschreiben, also 100% der Varianz erklären, weil die Originaldaten ja auch in einem 4 dimensionalen Raum sind).

Wie viele Prozent der totalen Varianz man mit den PCs genau erklären will, d.h., wie viele PCs man am Schluss behalten will, ist willkürlich und hängt vom Kontext ab. Die Grundidee ist der Kompromiss: Möglischst wenige PCs um möglichst viel totale Varianz zu erklären.

Angenommen, wir wollen in diesem Beispiel 80% der Varianz erklären. Wir haben gerade gesehen, dass wir dann 3 PCs behalten müssen. Die Koordinaten bzgl. der PC Basis sind in dem Listenelement \(x\) abgespeichert:

##             PC1       PC2        PC3        PC4
## [1,]  2.3444775 3.3495716 -2.0009272  1.1828421
## [2,]  1.4372454 0.8568585 -0.5569113 -0.5831169
## [3,] -6.3068138 2.7704720 -1.9365619 -0.7161288
## [4,]  0.5258753 2.0191090  4.5646573  0.3793131
## [5,]  0.1508849 1.8887760  2.7077596 -0.3738104
## [6,] -7.1845338 4.4622891 -1.8442804  0.8144265

Wenn wir also nur die Koordinaten der ersten 3 PCs behalten wollen, behalten wir also nur die ersten 3 Spalten von :

Manchmal visualisiert man auch die “cumulative proportion” in einem sog. Scree-Plot um einfacher zu sehen, wie viele PCs man behalten möchte. Z.B. so: