4 Linear Mixed Effects Models

4.1 Theorie in Kürze

Lineare Regression mit fixen Effekten (übliche \(\beta\)’s) und zufälligen Effekten (gruppenspezifische Störgrössen); fixed + zufällig = mixed.
Es werden die fixen Effekte und die Varianzen der zufälligen Effekte geschätzt; in diesem Prozess werden auch die modellierten zufälligen Effekte pro Person (bzw. Gruppe) gespeichert und können mit der Funktion ranef abgerufen werden.
Lineare Regression verlangte immer unabhängige Beobachtungen; bei den Mixed Models dürfen Beobachtungen innerhalb einer Gruppe (z.B. mehrere Messungen pro Person) korreliert sein; als Faustregel gilt: Für jede Gruppierung braucht man einen entsprechenden zufälligen Effekt.
Alternativ kann man pro Gruppierung eine Faktorvariable (“Blockfaktor”) in einer herkömmlichen Linearen Regression verwenden; beim Blockfaktor liegt der Fokus auf den Erwartungswerten der einzelnen Gruppen; beim Mixed Model liegt der Fokus der zu Grunde liegenden Population und der Streuung zwischen den einzelnen Gruppen.
Einfache Mixed Effects Modelle sind: Random Intercept Modell (RI) und Random Intercept and Random Slope Modell (RIRS).
RI-Modell (Person \(i\), Beobachtung \(j\)); geschätzt werden \(\beta_0\), \(\beta_1\), \(\sigma\), \(\sigma_u\): \[\begin{array}{c} Y_{ij} = (\beta_0 + u_i) + \beta_1 x_j + \varepsilon_{ij}, \\ \varepsilon_{ij} \sim N(0, \sigma^2),\\ u_i \sim N(0, \sigma_u^2) \end{array}\]
RIRS-Modell: (Person \(i\), Beobachtung \(j\)); geschätzt werden \(\beta_0\), \(\beta_1\), \(\sigma\), \(\sigma_1, \sigma_2, \rho\): \[\begin{array}{c} Y_{ij} = (\beta_0 + u_{1,i}) + (\beta_1 + u_{2,i})x_j + \varepsilon_{ij}, \\ \varepsilon_{ij} \sim N(0, \sigma^2), \\ \quad u_{1,i} \sim N(0, \sigma_1^2), \\ \quad u_{2,i} \sim N(0, \sigma_2^2), \\ cor(u_1, u_2) = \rho \end{array}\]
Residuenanalyse wie bei Linearer Regression; zudem sollte man prüfen, ob die modellierten Zufallseffekte ungefähr normalverteilt sind
Wichtige R Funktionen im Paket lme4 bzw. lmerTest: lmer, summary, predict, qqnorm, confint, ranef.

4.2 Bsp: RIRS-Modell

In diesem Beispiel schätzen wir ein RIRS-Modell mit den Daten der sleepstudy aus dem Paket lme4 (siehe ?sleepstudy für weitere Infos dazu). Eine Umsetzung mit dem Paket nlme findet man weiter unten.

library(lme4)
library(lmerTest)
fm <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)
summary(fm)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Reaction ~ Days + (Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1743.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9536 -0.4634  0.0231  0.4634  5.1793 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 612.10   24.741       
##           Days         35.07    5.922   0.07
##  Residual             654.94   25.592       
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)  251.405      6.825  17.000  36.838  < 2e-16 ***
## Days          10.467      1.546  17.000   6.771 3.26e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.138

confint(fm, oldNames = FALSE)

##                                    2.5 %      97.5 %
## sd_(Intercept)|Subject        14.3814732  37.7159917
## cor_Days.(Intercept)|Subject  -0.4815008   0.6849863
## sd_Days|Subject                3.8011643   8.7533851
## sigma                         22.8982669  28.8579965
## (Intercept)                  237.6806955 265.1295147
## Days                           7.3586533  13.5759188

Im Block Fixed effects sehen wir die geschätzten Populations-Mittelwerte. Die Interpretation in diesem Block ist analog zur Interpretation bei der linearen Regression. Die Zeile (Intercept) zeigt die durchschnittliche Reaktionszeit einer ausgeruhten Person (0 Tage Schlafentzug): \(251\) ms (95%-VI: \([237; 265]\) aus dem Output des Befehls ). Pro Tag Schlafentzug nimmt die erwartete Reaktionszeit gemäss unserem Modell um ca. \(10.5\) ms zu (95%-VI: \([7.4; 13.6]\)).

Im Block Random effects stehen die geschätzten Varianzen (und evtl. Korrelation) der zufälligen Effekte und des Fehlers (in der Zeile Residual). In diesem Fall haben wir eine Varianz für den unterschiedlichen Achsenabschnitt von Person zu Person (Random Intercept) und eine Varianz für die unterschiedliche Steigung von Person zu Person (Random Slope). Diese Werte stehen in der Spalte Variance. Daneben in der Spalte steht einfach die Wurzel der Varianzen (Achtung: Hier steht nicht der Standard Error wie wir es beim Output der linearen Regression gewöhnt sind, sondern wirklich nur die Wurzel aus der Spalte Variance). Die Standardabweichung (Spalte Std.Dev.) der Random Intercepts ist also ca. \(24.7\) ms (95%-VI: \([14.4; 37.7]\) ms). Eine typische Schwankung der mittleren Reaktionszeit im ausgeruhten Zustand von Person zu Person ist also ca. \(24.7\) ms. Die Standardabweichung der Schwankung bzgl. Steigung von Person zu Person ist ca. \(5.9\) (95%-VI: \([3.8; 8.8]\)). D.h., die Zunahme der Reationszeit pro Nacht mit Schlafentzug ist von Person zu Person unterschiedlich. Eine typische Schwankung der Steigung von Person zu Person ist ca. \(5.9\).

In der Spalte Corr der Random effects steht die Korrelation zwischen den zufälligen Schwankungen im Achsenabschnitt und in der Steigung. Sie wird zu \(0.07\) geschätzt (95%-VI: \([-0.48; 0.68]\)). D.h., es gibt keine nennenswerte Korrelation zwischen der Schwankung in dem Achsenabschnitt und der Schwankung in der Steigung von Person zu Person (angenommen, die Korrelation wäre nahe bei 1 gewesen: Das würde bedeuten, dass grosse Werte von \(u_1\) zusammen mit grossen Werten von \(u_2\) beobachtet werden; d.h., wenn jemand im ausgeruhten Zustand eine überdurchschnittlich lange Reaktionszeit hat, dann reagiert er besonders empfindlich auf Schlafentzug und die Steigung ist grösser als im Populationsmittel).

Die \(u\)’s im Modell wurden beim fitten des Modells für jede Person geschätzt (wenn man die Varianzen der zufälligen Effekte von Hand ausrechnet, ist das Ergebnis leicht anders als die Varianzen im summary-ouput, weil lmer eine andere Schätzmethode verwendet):

ranef(fm)

## $Subject
##     (Intercept)        Days
## 308   2.2585509   9.1989758
## 309 -40.3987381  -8.6196806
## 310 -38.9604090  -5.4488565
## 330  23.6906196  -4.8143503
## 331  22.2603126  -3.0699116
## 332   9.0395679  -0.2721770
## 333  16.8405086  -0.2236361
## 334  -7.2326151   1.0745816
## 335  -0.3336684 -10.7521652
## 337  34.8904868   8.6282652
## 349 -25.2102286   1.1734322
## 350 -13.0700342   6.6142178
## 351   4.5778642  -3.0152621
## 352  20.8636782   3.5360011
## 369   3.2754656   0.8722149
## 370 -25.6129993   4.8224850
## 371   0.8070461  -0.9881562
## 372  12.3145921   1.2840221
## 
## with conditional variances for "Subject"

Für alle Personen gelten im Modell die fixen Effekte \(\beta_0 \approx 251.4\) ms und \(\beta_1 \approx 10.5\) ms/Tag. Bei Person wurde eine individuelle Abweichung im Intercept von ca. \(2.3\) ms (etwas langsamer als der Durchschnitt) und eine individuelle Abweichung in der Steigung von ca. \(9.2\) ms/Tag (reagiert empfindlicher auf Schlafentzug als der Durchschnitt) gefittet. D.h., für Person 308 sieht die modellierte Gerade so aus: \[y = (251.4 + 2.3) + (10.5 + 9.2) \cdot \textrm{Days} = 253.7 + 19.7 \cdot \textrm{Days}.\]

Mit dem gefitteten Mixed Model können wir z.B. die Frage beantworten, wie unterschiedlich Personen auf Schlafentzug reagieren (mit der Standardabweichung der zufälligen Steigung, also ca. \(5.9\) ms; eine typische Schwankung von Person zu Person bzgl. Steigung ist also ungefähr \(6\) ms). Allerdings hat das Mixed Model auch Nachteile: Wir können z.B. nicht einfach ablesen, ob Person \(308\) im ausgeruhten Zustand eine signifikant grössere Reaktionszeit hat als z.B. Person \(335\). Für diese Frage wäre eine Lineare Regression mit einem Faktor für “Person” geeigneter. Zusammengefasst kann man sagen: Wenn man sich für die einzelnen Individuen der Studie interessiert, ist meist eine Lineare Regression mit Blockfaktoren günstig. Wenn man sich für die zu Grunde liegende Population interessiert, ist ein Mixed Model geeignet.

Die Vorhersage ist nun etwas komplizierter. Für eine konkrete neue Person wissen wir z.B. nicht, wie gross ihre individuellen zufälligen Effekte sind. Für schon beobachtete Personen haben wir zwar zufällige Effekte geschätzt (wie oben bei Person 308 erklärt), aber es ist nicht klar, wie genau diese zufälligen Effekte geschätzt wurden und somit ist nicht klar, wie genau die Vorhersage ist. Vorhersagen ohne Genauigkeitsangabe sind für beobachtete Personen allerdings möglich (es werden dann die geschätzten zufälligen Effekte verwendet). Welche Reaktionszeit sagt unser Modell z.B. für Person 308 nach 2.5 Tagen Schlafentzug voraus?

ndat <- data.frame(Days = 2.5, Subject = "308")
predict(fm, newdata = ndat)

##        1 
## 302.8293

## identisch mit Berechnung "von Hand" (abgesehen von Rundungsfehler)
(251.405 + 2.257) + (10.467 + 9.199)*2.5

## [1] 302.827

Die Residuenanalyse funktioniert grundsätzlich wie bei der linearen Regression. Zusätzlich müssen wir nun noch prüfen, ob die zufälligen Effekte (in etwa) normalverteilt sind:

library(sfsmisc)
mult.fig(mfrow= c(2,2))
plot(fitted(fm), residuals(fm), main = "TA") ## Tukey-Anscombe Plot
qqnorm(residuals(fm)) ## QQ-Plot fuer Residuen
rEff <- ranef(fm) ## Zuf?llige Achsenabschnitt und Steigung pro Person
qqnorm(rEff$Subject[,1]) ## QQ-Plot von zuf. Achsenabschnitt
qqnorm(rEff$Subject[,2]) ## QQ-Plot von zuf. Steigung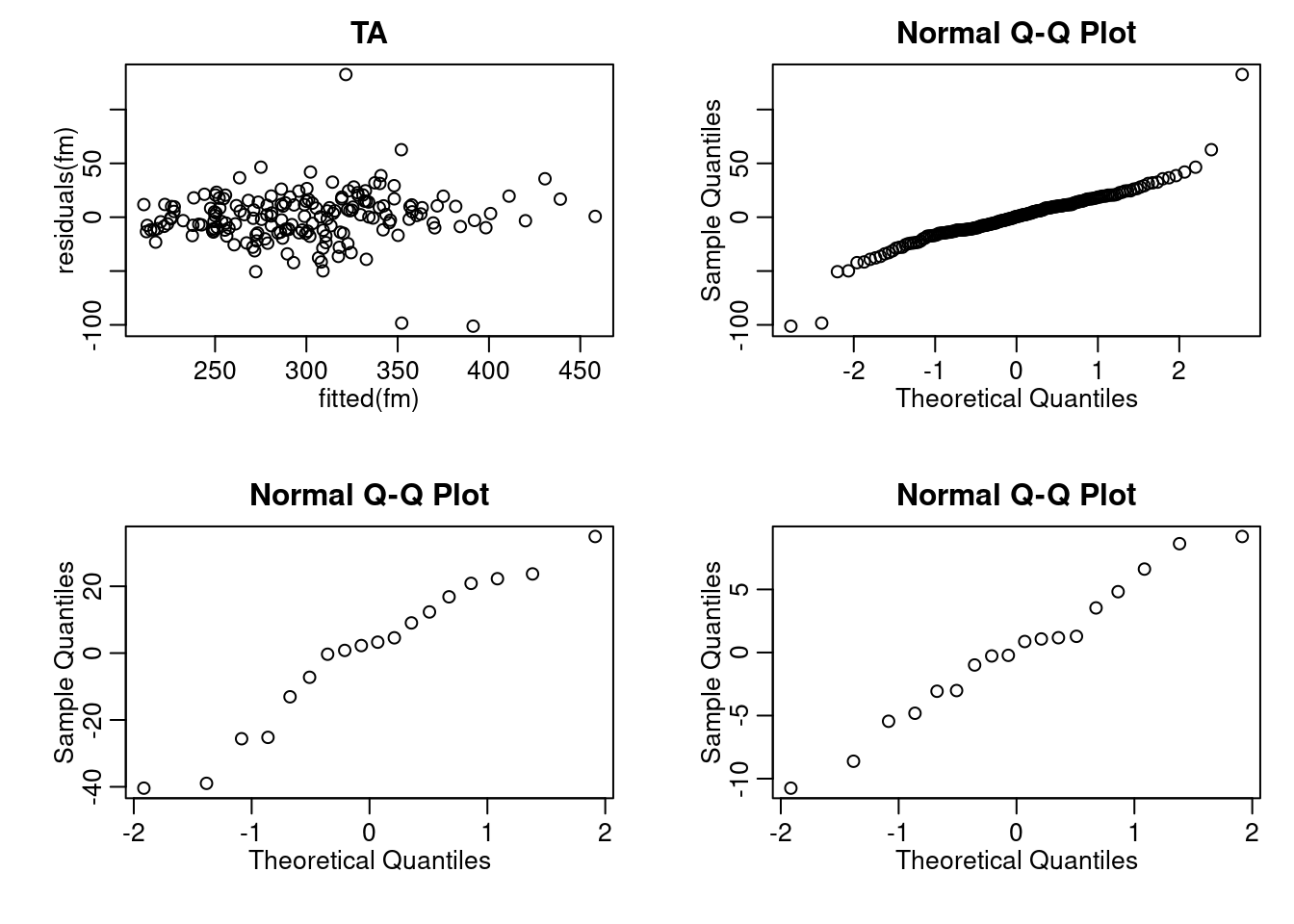

Umsetzung mit nlme

library(nlme)
fit <- lme(Reaction ~ Days, random = ~ 1 + Days | Subject, data = sleepstudy)
summary(fit)

## Linear mixed-effects model fit by REML
##  Data: sleepstudy 
##        AIC      BIC    logLik
##   1755.628 1774.719 -871.8141
## 
## Random effects:
##  Formula: ~1 + Days | Subject
##  Structure: General positive-definite, Log-Cholesky parametrization
##             StdDev    Corr  
## (Intercept) 24.740241 (Intr)
## Days         5.922103 0.066 
## Residual    25.591843       
## 
## Fixed effects: Reaction ~ Days 
##                 Value Std.Error  DF  t-value p-value
## (Intercept) 251.40510  6.824516 161 36.83853       0
## Days         10.46729  1.545783 161  6.77151       0
##  Correlation: 
##      (Intr)
## Days -0.138
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -3.95355735 -0.46339976  0.02311783  0.46339621  5.17925089 
## 
## Number of Observations: 180
## Number of Groups: 18

Wir erhalten die gleichen Resultate wie mit obigem Ansatz mit lme4.

Vertrauensintervalle erhalten wir hier mit der Funktion intervals.

intervals(fit)

## Approximate 95% confidence intervals
## 
##  Fixed effects:
##                  lower      est.     upper
## (Intercept) 237.927995 251.40510 264.88221
## Days          7.414662  10.46729  13.51991
## attr(,"label")
## [1] "Fixed effects:"
## 
##  Random Effects:
##   Level: Subject 
##                            lower        est.      upper
## sd((Intercept))       15.5175354 24.74024072 39.4443767
## sd(Days)               3.9041696  5.92210282  8.9830375
## cor((Intercept),Days) -0.5760831  0.06556383  0.6572156
## 
##  Within-group standard error:
##    lower     est.    upper 
## 22.79706 25.59184 28.72925

Diese Resultate unterscheiden sich leicht zu obigem Ansatz, weil verschiedene (statistische) Approximationen verwendet werden.